Materiewellen nach de Broglie: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
Zeile 10: Zeile 10:
  
 
Welche Wellenlängen haben dann zum Beispiel ein Elektron mit 10% der Lichtgeschwindigkeit und welche ein Fußball mit 10m/s?
 
Welche Wellenlängen haben dann zum Beispiel ein Elektron mit 10% der Lichtgeschwindigkeit und welche ein Fußball mit 10m/s?
−
 
+
:<math>\lambda=\frac{h}{p}=\frac{h}{m\,v}</math>
 
Elektron: <math>\lambda = 2{,}4\cdot10^{-11}\rm m</math> Im Bereich der Röntgenstrahlung.
 
Elektron: <math>\lambda = 2{,}4\cdot10^{-11}\rm m</math> Im Bereich der Röntgenstrahlung.
−
 
 
Fußball: <math>\lambda = 1{,}3\cdot10^{-34}\rm m</math> Extrem klein!
 
Fußball: <math>\lambda = 1{,}3\cdot10^{-34}\rm m</math> Extrem klein!
  
−
 
+
Um typische Welleneigenschaften, wie Beugung und Interferenz nachzuweisen, braucht man ein Doppelspalt oder ein Gitter in der Größenordnung der Wellenlänge. Für Elektronen kommen deshalb Kristallgitter in Frage, deren Atomabstände im Bereich der Wellenlänge von Röntgenstrahlung liegen.
  
 
==Elektronenbeugung Debey-Scherrer-Verfahren==
 
==Elektronenbeugung Debey-Scherrer-Verfahren==
Zeile 23: Zeile 22:
 
;Beobachtung
 
;Beobachtung
 
;Erklärung
 
;Erklärung
 +
Man nimmt an, das die Elektronen Welleneigenschaften haben, also verwenden wir das Huygensche Prinzip und die Interferenz von Wellen zur Erklärung.
  
 +
Die Atome sind in einem Kristall regelmäßig angeordnet. Wir betrachten den einfachen Fall von Atomebenen, die einen festen Abstand voneinander haben.
 +
 +
Jedes Atom im Kristall kann als Ausgangspunkt einer Elementarwelle gesehen werden. Die Elementarwellen ''einer'' Ebene überlagern sich dabei zu einer reflektierten Welle, nach dem Reflektionsgesetz <ref>Vgl. [[Reflektion und Brechung einer Welle]]</ref> und einer unverändert weiterlaufenden Welle.
 
====Animation: Braggsche Reflektionsbedingung====
 
====Animation: Braggsche Reflektionsbedingung====
 
Dargestellt sind zwei Atomebenen im Abstand d. Man kann den Winkel des einfallenden Elektronenstrahls durch Ziehen am grünen Punkt verändern.
 
Dargestellt sind zwei Atomebenen im Abstand d. Man kann den Winkel des einfallenden Elektronenstrahls durch Ziehen am grünen Punkt verändern.
Zeile 42: Zeile 45:
  
 
<ggb_applet width="736" height="740"  version="4.0" ggbBase64="UEsDBBQACAgIABS1PkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAAUtT5CAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1c25LbxhF9tr9iig+pXUfkzgVXe9eu1c2SS5ZUkuJKOeUHEBiSI4IAAoC75JafXZX/yAfk3W/5APsf8iXpmQFAgCC5JPdGK1FZwmWufbpPd88M6NNvZpMQXfA0E3F01iE93EE88uNARMOzzjQfdJ3ON19/fjrk8ZD3Uw8N4nTi5WcdQ9YUwVmHUubgwDG7BnX6XWMwGHT73KJdzBihgesSnw06CM0y8WUUv/YmPEs8n7/3R3zivYp9L1cDj/I8+fLk5PLyslcO1YvT4clw2O/NsqCDYJpRdtYpbr6E7hqNLpmqTjEmJ3/9/pXuviuiLPcin3eQFGEqvv78s9NLEQXxJboUQT466zjM6qARF8MRyESw43bQiayVACIJ93NxwTNoW3tUQueTpKOqeZEs/0zfobCSp4MCcSECnp51cM+wqeE4mDnUtk1CXBgyTgWP8qIyKQY9Kbs7vRD8Uvcr79SQRgflcRz2Pdkl+vlnRDHF6JG8EH2hcLEsXYT1O8z0heqLoS+mrmPo5oauaug6hq5jsA66EJnoh/ysM/DCDDAU0SAF/VXPWT4PuZpP8WIhPnkEMmXiCiozDIaiQZcI40fyrwV/DVlw0hSS1EbN0+mOg5ZDOsTZfkh6I0FZJaZrtsek5hoxrQ2Darm3kZOYNWhhKPWf+tsakW0Sc3lE/XyzAS3jXkQ8PSmpclqwA2UjWbewnpxPMskX5iLTlWZPkAncsGywchMRFy42RcAGRExkmPBIHGTJq42YDQUGYshBsh5hSJHDdOAfw1adWciEzuRbGziJCAxkIJMhojhlIGASUrwEjlIGNUwTmdBIDk+o7IJZyLDgiTnIgDlKStoEKjJoCM8wPEWMICYbExtRC1myP2JIqluOnDp0SZGFkUVkh8BqYLRmM9R3EJPSWAVcIkqmeQMifxKUt3mcVLqA2uCPFm5P+6eGV/zsNPT6PIRI8V5qEqELL5SMUAMN4ihHpRKpfjdMvWQk/Ow9z3NolaGP3oX3ysv57DnUzsqxVV0/jrK3aZw/icPpJMoQ8uMQV3OOQ1K7p9Ws4YHVCox6gVkrsGr39spxYyhB04zD+HGaldW9IHgpayxcAyD5Jgrnj1PujZNYNMU4PVFB55RP/VAEwot+AGOVo0hcUBWDpLsqY5BbguXHcRq8n2dgwWj2I09jgNZxZNSd6ycD055b++NIX+R7km8m7uH6HyD/vCgy3EYjF3iqhuMXlVa8GV8IOEwlm2sPL7PHcbh4pWR+4iX5NFUpA8wvlZKcR8OQK7tQLhbisT/ux7P32iCY7uvDPOGyiZpBf6iwRuAPqAnOdFhc+/qq6sipVbWwqoNVDVxamAiqcuJSVUNd+/qqaoHJ6qkVopJSTILLYUSmvBjuFFwpPZQ0eBndp5HIX5UPufDHhahEN3g9nfR5ZTbNPslt9Xl6smRXp2OeRjwszBiUOY2nmWZlzcIzMYzEQPhelA/EcJryrEFcTyruLzAV/Tbgw5SXIoQqMdPQqVJct9XWa9XV8zSevIwuPoBVtKeSeylYipgot6+LF9KV0pxmfioSaZuoDyFizBfWF4jMgwgT1Dkn+Qmd+KrLXOQSwqe8z+ddmRWmKU+Bx9N8FIOJvPXyFIBGr2H+Ey+K0FHmj6ZhMppnYnwpxqIX8GMYBnwUKEUyOeQTSNxQrixXGX+lwScqJZSqQnH/I7jJZRUvjAHKV5qxMngPxvdk3ljAGHpznjaAVf19HwfLcJdAgtNItN0knGuT0xOGmwS6U0xtOD2QP0Ozs06X9Bh4o7keHl3pJYFOiaWwkr8Nc9Fvl1QPlqlxaiGmTKIC5PdfFGTQcFo271HTMi0GWRPkoMSyDLswlVBm02giIoXVxIPJEgd/8e9/AWD9DKJEDosKMNVosajQPrvwsjZVEs1kRqq8KDheSuXdQMx4FQPBLMQVkMdr6Kuh1CI9ul6nBJfOaaFTsqVOybKryiFyjmF5kKmkMy88p7p5IYKAR1UbL/VralpjHDAThV1hIUcEdVFyjL5AR13cc+F6hf6MyPEqw6n5n0rLfjwB/gQoUvndyygHTwVgdRY5hwfRe3YOThDAgOA9V7cauGleVjjX/Ra9XcO38/34JjPTob709WVfwi1oU1pU97ZY08TzrZJ7FZbLAD7eBcDH+wFIqI7O6noQTosV8N8N+u+8+RL259qGH7fg9zbDn0JPJbZeG/yGY6lJWge/So2w0fIte5tvt7JfViC46GyVAzI3OyD+90g3yXQCIyZJKHyRV3CFUpmVkwDlt7OUMeeJTA/fRB9SL8rkttNyfrBOX09E6kOQWamyJy2V+ZtVBtmE8Cul+NcxZo3Wmqnq3hpbqQx6jTLEkEcXMFVYxiA0w8Um3xyXdCnfzEhlCKR4dUVqXJrIXGmGzsv652Wtc6ryBhcCdn1hAQWsGOPcKLs+N2tiL9uJXFvKzLSVQswSyFLlDmUJ85s0zy74GGTqICiF+PWKR8N89LcnP32Ffv+lCltabr2abeq1LGl3eOMk7lYoCXkYMxzqGq7jMGyTwr8xExPHdC1mUhszuXC8lqzX2Ectdy/UkMShl+4ekI7wI4SPNc1qcC7z7ekuEerpnhEK65WfSR5GIbcbf1b6s6caaMiXWwhPdvFok/u09zeDQcZzlYMbOt44f0x3R3qOtdnbtc1Fur7uCoPZyRVul2f72jgmLdN4pguew4XKXQYP5rwLH58dTspNeoAfcalrYYZNCWrBSJO5hsmoQwnF1JEb37e+im2C8vyeQVmwyNUkIsbWLswmBgXMsOOCAVsFYsRksORmBgU4iUsc+w6c2PciTYvgurDT59ocz1t2+vxPXhJnX+1immWTgzHQ7mq4uw+I97N1eD/bHe9nB4j3So/QvSOXsJwRhfNhHK0GvPC3JWTK7dZMvKGKHwQM4Y+Jbsl1y4Fuw6sO5MnGdjrT0yrVUfW+Nr7izfF15wUrGPu6XMzcRdXrvXHGh/Kpmgjfb2W9YaI32Bdijuk4rgu5AnWwS4q8B3wAJpSBE8Cmy4ghj9uvtKkahm1Zrmm6Jlwx25AJXaOpe1+Fb9bK4JC0YrkME8uiBiPUsE2dzHdpzzKIRSk1ifwswnA+eaXwdU78oVTTXceY7v8iZQ5QOyuZ80kSp7XplPJByMey66VNp6c/fYUo+gKpM2942n37qdb1g24wNpZXmFLblGQzTMeSR/YqcFm2DUoltgsLWwfSqnvbgdqUjH77CRy9kp5FFcZWz7yvXaRiV/zbVhY63GUPabifh/r0N8UNo+cAW25xJ7yhhWg64WlND8HyaTor+9/3/Fp/OKPOmvY9wV51cM+2PLMnuDyzJzYtD+0dvOWh/V5n5+1j8jaV8Soqr2feK5jHat49bfFutJl3UqRKdaNDiRWrdjWlqtp7oDcNFZuygP1cX9BSwXgX1zf+/4HgGt/nqrtb8ntNfb5J81E8jCMvXE+tUUuvYgdqiYOh1spjp5WEexhurTuCGGs1iJYaXuiCl7vsNb44oF1G3LMtQm3mMGbD8obYxQrIBX1gRk2HUduCNeqdHzu8PBxQVmPSvStQWiuzICtWZJBVHMmV2OzoxfHxqnVXK2XKlnMm0jNhHSuXrbD4Ac4Z27Oc7Jau/fbrirH3y9c2fRV0g3yNFPmauXO+xv646dp13zbU1urLvu3dLk7t3eHwd7fF/j19XfeuBW9/M7z1r+v6D7okbe6YtTCcr0Z8+wBOD2SPbG9Nftxekx+31ySk5oHQ3kD+LKeoLWMCKOME/fYr6qI0nkZB+Xx8jP7zj39KH9dPucjv8XPL2zOKQ/sWsx2dQexoGg2LEN1UwDYxumzfCpb4zkLzwiKWBgVdrArRN1oc7Bigt9hr3DHircvhh5q+H1v0/U4X7BLtvntQGpeHIbdA4zz1fN40/zq3zZ7DLEIc4tpAYcgjFbNZjzqO4TDTdS3LJY5l3cHyoB/HIfcWZ/3JsvHe9PcsN/jcz9Q4ONbGD/7KXwk20kVd4iWLn4i99aZtk96MxdXhYGEY7i1i8SMYfDhNtnDDOc/ywgerH/ts43pVm7YLXL9hvIXnvXZztJ5sHxF1v+yAPH9UWsBW+zm6/mGkhOVvLchWP7WoFkDsZrs2J/WfRcrn8n+z8fV/AVBLBwgMNEcrFQwAAANEAABQSwECFAAUAAgICAAUtT5CRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIABS1PkIMNEcrFQwAAANEAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAArQwAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
 
<ggb_applet width="736" height="740"  version="4.0" ggbBase64="UEsDBBQACAgIABS1PkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAAUtT5CAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1c25LbxhF9tr9iig+pXUfkzgVXe9eu1c2SS5ZUkuJKOeUHEBiSI4IAAoC75JafXZX/yAfk3W/5APsf8iXpmQFAgCC5JPdGK1FZwmWufbpPd88M6NNvZpMQXfA0E3F01iE93EE88uNARMOzzjQfdJ3ON19/fjrk8ZD3Uw8N4nTi5WcdQ9YUwVmHUubgwDG7BnX6XWMwGHT73KJdzBihgesSnw06CM0y8WUUv/YmPEs8n7/3R3zivYp9L1cDj/I8+fLk5PLyslcO1YvT4clw2O/NsqCDYJpRdtYpbr6E7hqNLpmqTjEmJ3/9/pXuviuiLPcin3eQFGEqvv78s9NLEQXxJboUQT466zjM6qARF8MRyESw43bQiayVACIJ93NxwTNoW3tUQueTpKOqeZEs/0zfobCSp4MCcSECnp51cM+wqeE4mDnUtk1CXBgyTgWP8qIyKQY9Kbs7vRD8Uvcr79SQRgflcRz2Pdkl+vlnRDHF6JG8EH2hcLEsXYT1O8z0heqLoS+mrmPo5oauaug6hq5jsA66EJnoh/ysM/DCDDAU0SAF/VXPWT4PuZpP8WIhPnkEMmXiCiozDIaiQZcI40fyrwV/DVlw0hSS1EbN0+mOg5ZDOsTZfkh6I0FZJaZrtsek5hoxrQ2Darm3kZOYNWhhKPWf+tsakW0Sc3lE/XyzAS3jXkQ8PSmpclqwA2UjWbewnpxPMskX5iLTlWZPkAncsGywchMRFy42RcAGRExkmPBIHGTJq42YDQUGYshBsh5hSJHDdOAfw1adWciEzuRbGziJCAxkIJMhojhlIGASUrwEjlIGNUwTmdBIDk+o7IJZyLDgiTnIgDlKStoEKjJoCM8wPEWMICYbExtRC1myP2JIqluOnDp0SZGFkUVkh8BqYLRmM9R3EJPSWAVcIkqmeQMifxKUt3mcVLqA2uCPFm5P+6eGV/zsNPT6PIRI8V5qEqELL5SMUAMN4ihHpRKpfjdMvWQk/Ow9z3NolaGP3oX3ysv57DnUzsqxVV0/jrK3aZw/icPpJMoQ8uMQV3OOQ1K7p9Ws4YHVCox6gVkrsGr39spxYyhB04zD+HGaldW9IHgpayxcAyD5Jgrnj1PujZNYNMU4PVFB55RP/VAEwot+AGOVo0hcUBWDpLsqY5BbguXHcRq8n2dgwWj2I09jgNZxZNSd6ycD055b++NIX+R7km8m7uH6HyD/vCgy3EYjF3iqhuMXlVa8GV8IOEwlm2sPL7PHcbh4pWR+4iX5NFUpA8wvlZKcR8OQK7tQLhbisT/ux7P32iCY7uvDPOGyiZpBf6iwRuAPqAnOdFhc+/qq6sipVbWwqoNVDVxamAiqcuJSVUNd+/qqaoHJ6qkVopJSTILLYUSmvBjuFFwpPZQ0eBndp5HIX5UPufDHhahEN3g9nfR5ZTbNPslt9Xl6smRXp2OeRjwszBiUOY2nmWZlzcIzMYzEQPhelA/EcJryrEFcTyruLzAV/Tbgw5SXIoQqMdPQqVJct9XWa9XV8zSevIwuPoBVtKeSeylYipgot6+LF9KV0pxmfioSaZuoDyFizBfWF4jMgwgT1Dkn+Qmd+KrLXOQSwqe8z+ddmRWmKU+Bx9N8FIOJvPXyFIBGr2H+Ey+K0FHmj6ZhMppnYnwpxqIX8GMYBnwUKEUyOeQTSNxQrixXGX+lwScqJZSqQnH/I7jJZRUvjAHKV5qxMngPxvdk3ljAGHpznjaAVf19HwfLcJdAgtNItN0knGuT0xOGmwS6U0xtOD2QP0Ozs06X9Bh4o7keHl3pJYFOiaWwkr8Nc9Fvl1QPlqlxaiGmTKIC5PdfFGTQcFo271HTMi0GWRPkoMSyDLswlVBm02giIoXVxIPJEgd/8e9/AWD9DKJEDosKMNVosajQPrvwsjZVEs1kRqq8KDheSuXdQMx4FQPBLMQVkMdr6Kuh1CI9ul6nBJfOaaFTsqVOybKryiFyjmF5kKmkMy88p7p5IYKAR1UbL/VralpjHDAThV1hIUcEdVFyjL5AR13cc+F6hf6MyPEqw6n5n0rLfjwB/gQoUvndyygHTwVgdRY5hwfRe3YOThDAgOA9V7cauGleVjjX/Ra9XcO38/34JjPTob709WVfwi1oU1pU97ZY08TzrZJ7FZbLAD7eBcDH+wFIqI7O6noQTosV8N8N+u+8+RL259qGH7fg9zbDn0JPJbZeG/yGY6lJWge/So2w0fIte5tvt7JfViC46GyVAzI3OyD+90g3yXQCIyZJKHyRV3CFUpmVkwDlt7OUMeeJTA/fRB9SL8rkttNyfrBOX09E6kOQWamyJy2V+ZtVBtmE8Cul+NcxZo3Wmqnq3hpbqQx6jTLEkEcXMFVYxiA0w8Um3xyXdCnfzEhlCKR4dUVqXJrIXGmGzsv652Wtc6ryBhcCdn1hAQWsGOPcKLs+N2tiL9uJXFvKzLSVQswSyFLlDmUJ85s0zy74GGTqICiF+PWKR8N89LcnP32Ffv+lCltabr2abeq1LGl3eOMk7lYoCXkYMxzqGq7jMGyTwr8xExPHdC1mUhszuXC8lqzX2Ectdy/UkMShl+4ekI7wI4SPNc1qcC7z7ekuEerpnhEK65WfSR5GIbcbf1b6s6caaMiXWwhPdvFok/u09zeDQcZzlYMbOt44f0x3R3qOtdnbtc1Fur7uCoPZyRVul2f72jgmLdN4pguew4XKXQYP5rwLH58dTspNeoAfcalrYYZNCWrBSJO5hsmoQwnF1JEb37e+im2C8vyeQVmwyNUkIsbWLswmBgXMsOOCAVsFYsRksORmBgU4iUsc+w6c2PciTYvgurDT59ocz1t2+vxPXhJnX+1immWTgzHQ7mq4uw+I97N1eD/bHe9nB4j3So/QvSOXsJwRhfNhHK0GvPC3JWTK7dZMvKGKHwQM4Y+Jbsl1y4Fuw6sO5MnGdjrT0yrVUfW+Nr7izfF15wUrGPu6XMzcRdXrvXHGh/Kpmgjfb2W9YaI32Bdijuk4rgu5AnWwS4q8B3wAJpSBE8Cmy4ghj9uvtKkahm1Zrmm6Jlwx25AJXaOpe1+Fb9bK4JC0YrkME8uiBiPUsE2dzHdpzzKIRSk1ifwswnA+eaXwdU78oVTTXceY7v8iZQ5QOyuZ80kSp7XplPJByMey66VNp6c/fYUo+gKpM2942n37qdb1g24wNpZXmFLblGQzTMeSR/YqcFm2DUoltgsLWwfSqnvbgdqUjH77CRy9kp5FFcZWz7yvXaRiV/zbVhY63GUPabifh/r0N8UNo+cAW25xJ7yhhWg64WlND8HyaTor+9/3/Fp/OKPOmvY9wV51cM+2PLMnuDyzJzYtD+0dvOWh/V5n5+1j8jaV8Soqr2feK5jHat49bfFutJl3UqRKdaNDiRWrdjWlqtp7oDcNFZuygP1cX9BSwXgX1zf+/4HgGt/nqrtb8ntNfb5J81E8jCMvXE+tUUuvYgdqiYOh1spjp5WEexhurTuCGGs1iJYaXuiCl7vsNb44oF1G3LMtQm3mMGbD8obYxQrIBX1gRk2HUduCNeqdHzu8PBxQVmPSvStQWiuzICtWZJBVHMmV2OzoxfHxqnVXK2XKlnMm0jNhHSuXrbD4Ac4Z27Oc7Jau/fbrirH3y9c2fRV0g3yNFPmauXO+xv646dp13zbU1urLvu3dLk7t3eHwd7fF/j19XfeuBW9/M7z1r+v6D7okbe6YtTCcr0Z8+wBOD2SPbG9Nftxekx+31ySk5oHQ3kD+LKeoLWMCKOME/fYr6qI0nkZB+Xx8jP7zj39KH9dPucjv8XPL2zOKQ/sWsx2dQexoGg2LEN1UwDYxumzfCpb4zkLzwiKWBgVdrArRN1oc7Bigt9hr3DHircvhh5q+H1v0/U4X7BLtvntQGpeHIbdA4zz1fN40/zq3zZ7DLEIc4tpAYcgjFbNZjzqO4TDTdS3LJY5l3cHyoB/HIfcWZ/3JsvHe9PcsN/jcz9Q4ONbGD/7KXwk20kVd4iWLn4i99aZtk96MxdXhYGEY7i1i8SMYfDhNtnDDOc/ywgerH/ts43pVm7YLXL9hvIXnvXZztJ5sHxF1v+yAPH9UWsBW+zm6/mGkhOVvLchWP7WoFkDsZrs2J/WfRcrn8n+z8fV/AVBLBwgMNEcrFQwAAANEAABQSwECFAAUAAgICAAUtT5CRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIABS1PkIMNEcrFQwAAANEAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAArQwAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
 +
 +
==Fußnoten==
 +
<references />
  
 
==Links==
 
==Links==

Version vom 31. Januar 2013, 14:32 Uhr

Um alle Phänomene von Licht zu beschreiben, mußten wir sowohl auf das Teilchen-, als auch auf das Wellenmodell zurückgreifen.

Einerseits beschreiben wir die Ausbreitung von gekoppelten elektrischen und magnetischen Feldern, andererseits sprechen wir von Photonen, die eine gewisse Energiemenge enthalten, eine Masse und einen Impuls besitzen.

Es stellt sich daher die Frage, ob nicht auch Gegenstände, die bisher im Teilchenmodell beschrieben wurden, auch Welleneigenschaften haben. Wie zum Beispiel Moleküle, Atome, Atomkerne, Elektronen, usw.

Welche Frequenz oder Wellenlänge sollte dann so einer Welle zugeordnet werden? Bisher kennen wir nur die Energie, Masse und den Impuls eines Photons:

[math]E=m\,c^2=h\,f \qquad p=\frac{h}{\lambda}[/math]

Bei der Berechnung der Energie und der Masse ist es wesentlich, dass das Photon sich mit Lichtgeschwindigkeit ausbreitet. Dies ist aber bei Atomen und anderen Teilchen nie der Fall, daher ist es sinnvoll den Zusammenhang von Impuls und Wellenlänge zu verallgemeinern.

Welche Wellenlängen haben dann zum Beispiel ein Elektron mit 10% der Lichtgeschwindigkeit und welche ein Fußball mit 10m/s?

[math]\lambda=\frac{h}{p}=\frac{h}{m\,v}[/math]

Elektron: [math]\lambda = 2{,}4\cdot10^{-11}\rm m[/math] Im Bereich der Röntgenstrahlung. Fußball: [math]\lambda = 1{,}3\cdot10^{-34}\rm m[/math] Extrem klein!

Um typische Welleneigenschaften, wie Beugung und Interferenz nachzuweisen, braucht man ein Doppelspalt oder ein Gitter in der Größenordnung der Wellenlänge. Für Elektronen kommen deshalb Kristallgitter in Frage, deren Atomabstände im Bereich der Wellenlänge von Röntgenstrahlung liegen.

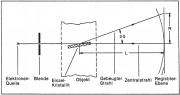
Elektronenbeugung Debey-Scherrer-Verfahren

Aufbau
Versuchsaufbau Elektronenbeugung


Beobachtung
Erklärung

Man nimmt an, das die Elektronen Welleneigenschaften haben, also verwenden wir das Huygensche Prinzip und die Interferenz von Wellen zur Erklärung.

Die Atome sind in einem Kristall regelmäßig angeordnet. Wir betrachten den einfachen Fall von Atomebenen, die einen festen Abstand voneinander haben.

Jedes Atom im Kristall kann als Ausgangspunkt einer Elementarwelle gesehen werden. Die Elementarwellen einer Ebene überlagern sich dabei zu einer reflektierten Welle, nach dem Reflektionsgesetz [1] und einer unverändert weiterlaufenden Welle.

Animation: Braggsche Reflektionsbedingung

Dargestellt sind zwei Atomebenen im Abstand d. Man kann den Winkel des einfallenden Elektronenstrahls durch Ziehen am grünen Punkt verändern.

Nur bei bestimmten Winkeln ist der Gangunterschied ein Vielfaches der Wellenlänge. Für diese Fälle liegt konstruktive Interferenz vor.


Bitte installiere Java, um diese Seite nutzen zu können.
Interferenzbedingungen


Animation: Maxima des Debey-Scherrer-Verfahrens / Pulver-Verfahrens

Dargestellt ist einer der vielen kleinen Kristalle des Pulvers. Der Kristall kann in seiner Lage durch die Angabe des Winkels [math]\varphi[/math] verändert werden.

Für manche Winkel ist die Braggsche Interferenzbedingung für das erste, zweite, usw. Maxima erfüllt. Im Pulver sind die kleinen Kristalle in allen möglichen Lagen vorhanden, weswegen es auch für alle Winkel Kristalle gibt, welche die Interferenzbedingung erfüllen.

Trifft der Elektronenstrahl auf den fluoreszierenden Schirm, so sieht man dort einen Fleck.

Bitte installiere Java, um diese Seite nutzen zu können.

Fußnoten

  1. ↑ Vgl. Reflektion und Brechung einer Welle

Links

Von „http://schulphysikwiki.de/index.php?title=Materiewellen_nach_de_Broglie&oldid=5609“