Noch mehr Aufgaben zur Newtonschen Mechanik 10b (Lösungen): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „====Roller fahren==== 100px Die Impulsänderungen betragen: :<math>\triangle p = F \, \triangle t = 100 \, \rm N \cdot 1\, s = 100 …“) |
(→Roller fahren) |
||
| Zeile 7: | Zeile 7: | ||
Tina hat nach dem ersten Anschubsen eine Impulsmenge von 100Hy, nach dem zweiten Anschubsen von 130Hy: | Tina hat nach dem ersten Anschubsen eine Impulsmenge von 100Hy, nach dem zweiten Anschubsen von 130Hy: | ||
:<math>p(\rm 1\, s)=100\, Hy </math> <math>.\qquad p(\rm 3{,}5\, s)=130\, Hy .</math> | :<math>p(\rm 1\, s)=100\, Hy </math> <math>.\qquad p(\rm 3{,}5\, s)=130\, Hy .</math> | ||
| − | + | Die Geschwindigkeiten erhält man durch Division mit der Masse: | |
| − | + | :<math>p=m\, v \quad \Rightarrow \quad v = \frac{p}{m}</math> | |
| + | :<math>v(\rm 1\, s)=\frac{100\, Hy}{50 \, kg}= 2\,\frac{m}{s}\approx 7\, \frac{km}{h} </math> <math>.\qquad v(\rm 3{,}5\, s)=\frac{130\, Hy}{50 \, kg}= 2{,}6\,\frac{m}{s}\approx 9{,}5\, \frac{km}{h}.</math> | ||
*Wieviel Impuls hat Tina nach dem ersten und nach dem zweiten Anschubsen und wie schnell ist sie jeweils? (Rechne ohne Reibung, also ohne Impulsverlust.) | *Wieviel Impuls hat Tina nach dem ersten und nach dem zweiten Anschubsen und wie schnell ist sie jeweils? (Rechne ohne Reibung, also ohne Impulsverlust.) | ||
| Zeile 16: | Zeile 17: | ||
*Wie lange nach dem zweimaligen Anschubsen kann Tina noch rollen, bevor sie stehen bleibt? | *Wie lange nach dem zweimaligen Anschubsen kann Tina noch rollen, bevor sie stehen bleibt? | ||
*Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren? | *Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren? | ||
| − | |||
====Widerstände beim Radfahren==== | ====Widerstände beim Radfahren==== | ||
Version vom 4. Februar 2014, 10:02 Uhr
Roller fahren
Die Impulsänderungen betragen:
- [math]\triangle p = F \, \triangle t = 100 \, \rm N \cdot 1\, s = 100 \, Hy[/math]
- [math]\triangle p = F \, \triangle t = 60\, \rm N \cdot 0{,}5 \, s = 30 \, Hy[/math]
Tina hat nach dem ersten Anschubsen eine Impulsmenge von 100Hy, nach dem zweiten Anschubsen von 130Hy:
- [math]p(\rm 1\, s)=100\, Hy [/math] [math].\qquad p(\rm 3{,}5\, s)=130\, Hy .[/math]
Die Geschwindigkeiten erhält man durch Division mit der Masse:
- [math]p=m\, v \quad \Rightarrow \quad v = \frac{p}{m}[/math]
- [math]v(\rm 1\, s)=\frac{100\, Hy}{50 \, kg}= 2\,\frac{m}{s}\approx 7\, \frac{km}{h} [/math] [math].\qquad v(\rm 3{,}5\, s)=\frac{130\, Hy}{50 \, kg}= 2{,}6\,\frac{m}{s}\approx 9{,}5\, \frac{km}{h}.[/math]
- Wieviel Impuls hat Tina nach dem ersten und nach dem zweiten Anschubsen und wie schnell ist sie jeweils? (Rechne ohne Reibung, also ohne Impulsverlust.)
- Zeichne das Impuls-Zeit- und Kraft-Zeit-Diagramm für die drei Sekunden dauernde Fahrt. Zeichne das passende Geschwindigkeit-Zeit-Diagramm.
Die gerade eben noch vernachlässigte Reibungskraft beträgt für Tina und ihren Roller konstant 10 Newton.
- Wie lange nach dem zweimaligen Anschubsen kann Tina noch rollen, bevor sie stehen bleibt?
- Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren?
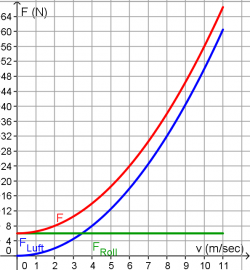
Widerstände beim Radfahren
In diesem Widerstandsdiagramm ist die Reibungskraft F über die Geschwindigkeit aufgetragen. Die Reibungskraft setzt sich aus dem geschwindigkeitsunabhängigen Rollwiderstand und der Luftreibung zusammen.
Paula fährt auf ebener Strecke mit einer konstanten Geschwindigkeit von 6 m/s.
- Wie groß ist jetzt die Reibungskraft und wie groß die antreibende Kraft?
Danach tritt Paula so in die Pedale, dass die antreibende Kraft auf 40N ansteigt.
- Wie schnell wird sie jetzt?
Turmspringen
Eine Turmspringerin läßt sich vom 10-Meter-Turm fallen. Sie hat eine Masse von 60 kg.
- Mit welcher Kraft wird sie beschleunigt?
- Wie groß ist ihr Impuls und ihre Geschwindigkeit nach 1, 2, 3 Sekunden? (nach t Sekunden?)
- Vergleiche mit dem Fall ihres um 20kg "schwereren" Vereinskameraden.
- die Impuls- und Geschwindigkeitszunahme,
- den Aufprall auf der Wasseroberfläche.
- Zeichne für beide die Geschwindigkeit-Zeit-, Impuls-Zeit- und Kraft-Zeit-Diagramme.