Noch mehr Aufgaben zur Newtonschen Mechanik 10b (Lösungen): Unterschied zwischen den Versionen

Version vom 4. Februar 2014, 13:07 Uhr

Roller fahren

Tina steht mit ihrem Roller auf einer ebenen Straße. Zusammen haben sie eine Masse von 50kg. Dann schubst sie sich zweimal von der Straße ab. Beim ersten Mal eine Sekunde lang mit einer Kraft von 100N, beim zweiten Mal eine halbe Sekunde lang mit einer Kraft von 60N. Dazwischen rollt sie für zwei Sekunden.

• Wieviel Impuls hat Tina nach dem ersten und nach dem zweiten Anschubsen und wie schnell ist sie jeweils? (Rechne ohne Reibung, also ohne Impulsverlust.)

Die Impulsänderungen betragen:

[math]\triangle p = F \, \triangle t = 100 \, \rm N \cdot 1\, s = 100 \, Hy[/math]

[math]\triangle p = F \, \triangle t = 60\, \rm N \cdot 0{,}5 \, s = 30 \, Hy[/math]

Tina hat nach dem ersten Anschubsen eine Impulsmenge von 100Hy, nach dem zweiten Anschubsen von 130Hy:

[math]p(\rm 1\, s)=100\, Hy [/math] [math].\qquad p(\rm 3{,}5\, s)=130\, Hy .[/math]

Die Geschwindigkeiten erhält man durch Division durch die Masse:

[math]p=m\, v \quad \Rightarrow \quad v = \frac{p}{m}[/math]

[math]v(\rm 1\, s)=\frac{100\, Hy}{50 \, kg}= 2\,\frac{m}{s}\approx 7\, \frac{km}{h} [/math] [math].\qquad v(\rm 3{,}5\, s)=\frac{130\, Hy}{50 \, kg}= 2{,}6\,\frac{m}{s}\approx 9{,}5\, \frac{km}{h}.[/math]

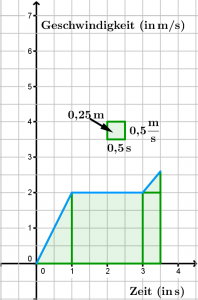
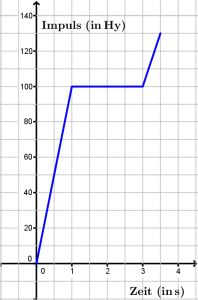
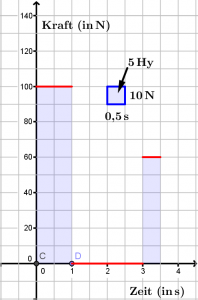
• Zeichne das Impuls-Zeit- und Kraft-Zeit-Diagramm für die drei Sekunden dauernde Fahrt. Zeichne das passende Geschwindigkeit-Zeit-Diagramm.

• Bewegungsdiagramme
• 

  Geschwindigkeit-Zeit-Diagramm

• 

  Impuls-Zeit-Diagramm

• 
• 

  Kraft-Zeit-Diagramm

Die gerade eben noch vernachlässigte Reibungskraft beträgt für Tina und ihren Roller konstant 10 Newton.

• Wie lange nach dem zweimaligen Anschubsen kann Tina noch rollen, bevor sie stehen bleibt?

Wenn man die Reibungskraft während der ersten 3,5s vernachlässigt, hat Tina einen Impuls von 130Hy. Die Impulsänderung bis zum Stillstand beträgt auch 130Hy. Die bremsende Kraft von 10N verringert den Impuls um 10Huygens pro Sekunde:

[math]\triangle p = F \, \triangle t[/math]

[math]130\, \rm Hy = 10\, N \cdot \triangle t \quad \Rightarrow \quad \triangle t = \frac{130\, \rm Hy }{10\, N } = 10\, s[/math]

Tina kann also noch 10 Sekunden lang ausrollen.

Berücksichtigt man die Reibungskraft auch schon während der ersten 3,5s, dann kann man in der obigen Rechnung von Tinas abstoßender Kraft jeweils 10N abziehen und rechnet nun mit 90N und 50N.

Oder man überlegt sich, dass Tina nun auch schon während der Anfangsphase pro Sekunde 10 Huygens Impuls verliert. Nach dem 3,5 Sekunden andauernden zweimaligen Anschubsen rollt sie daher nur noch 6,5 Sekunden lang weiter.

• Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren?

Tina muss im Durchschnitt 10 Hugens pro Sekunde Impuls erhalten, denn soviel geht durch die Reibung verloren.

Sie könnte sich eine Sekunde lang mit 20 Newton abstoßen, dann eine Sekunde lang rollen und so weiter.

Oder sie stößt sich eine Sekunde lang mit 30 Newton ab, dann kann sie zwei Sekunden lang rollen und so weiter.

Widerstände beim Radfahren

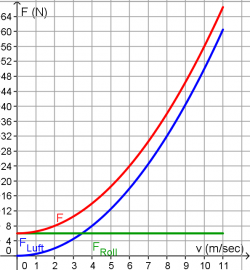
In diesem Widerstandsdiagramm ist die Reibungskraft F über die Geschwindigkeit aufgetragen. Die Reibungskraft setzt sich aus dem geschwindigkeitsunabhängigen Rollwiderstand und der Luftreibung zusammen.

Paula fährt auf ebener Strecke mit einer konstanten Geschwindigkeit von 6 m/s.

• Wie groß ist jetzt die Reibungskraft und wie groß die antreibende Kraft?

Wenn Paula mit einer konstanten Geschwindigkeit fährt, dann verändert sich auch der Impuls nicht. Deshalb muss durch Paulas antreibende Kraft genausoviel Impuls reingehen, wie durch die Reibungskraft wieder rausgeht.

Beide Krafte sind also gleich groß, Paula ist im "Kräftegleichgewicht".

Am Diagramm kann man ablesen, dass die gesamte Reibungskraft bei 6 m/s gerade 24N beträgt. Paula treibt sich also mit einer Kraft von 24N an.

Danach tritt Paula so in die Pedale, dass die antreibende Kraft auf 40N ansteigt.

• Wie schnell wird sie jetzt?

Auch jetzt wird sie so schnell, dass wieder Kräftegleichgewicht eintritt. Das ist bei einer Geschwindigkeit von ca. 8,2 m/s (30 km/h) der Fall.

Turmspringen

Eine Turmspringerin läßt sich vom 10-Meter-Turm fallen. Sie hat eine Masse von 60 kg.

• Mit welcher Kraft wird sie beschleunigt?

Ihre Gewichtskraft beträgt:

[math]F_G = m \, g = 60\, \rm kg \cdot 10\,\frac{N}{kg} = 600\, N[/math]

• Wie groß ist ihr Impuls und ihre Geschwindigkeit nach 1, 2, 3 Sekunden? (nach t Sekunden?)

Ihr Impuls nimmt immer mit 600 Huygens pro Sekunde zu.

[math]\triangle p = F \cdot \triangle t= 600 \, \rm N \cdot \triangle t[/math]

[math]p(1\, \rm s)= 600\, Hy[/math]

[math]p(2\, \rm s)= 1200\, Hy[/math]

[math]p(3\, \rm s)= 1800\, Hy[/math]

• Vergleiche mit dem Fall ihres um 20kg "schwereren" Vereinskameraden.
  • die Impuls- und Geschwindigkeitszunahme,

Seine Gewichtskraft beträgt 800N, daher nimmt sein Impuls immer mit 800 Huygens pro Sekunde zu:

[math]\triangle p = F \cdot \triangle t= 600 \, \rm N \cdot \triangle t[/math]

[math]p(1\, \rm s)= 800\, Hy[/math]

[math]p(2\, \rm s)= 1600\, Hy[/math]

[math]p(3\, \rm s)= 2400\, Hy[/math]

Die Geschwindigkeit erhält man durch Division durch die Masse von 80kg:

[math]v(1\, \rm s)= 10\, m/s[/math]

[math]v(2\, \rm s)= 20\, m/s[/math]

[math]v(3\, \rm s)= 30\, m/s[/math]

Aha! Die Turmsprimgerin erhält zwar nur weniger Impuls, aber sie benötigt auch weniger, um auf die gleiche Geschwindigkeit zu kommen!

Einerseits hat sie durch ihre kleinere Masse eine geringere beschleunigende Kraft, aber andererseits ist sie durch ihre geringere Masse auch weniger träge. Beide Effekte gleichen sich genau aus.

Man kann das auch nachrechnen. Die Gewichtskraft beträgt:

[math]F_G=m \, g[/math]

Der Impuls nach der Zeit t beträgt also:

[math] p = F \cdot t= m \, g \, t[/math]

Daraus folgt für die Geschwindigkeit:

[math] v = \frac{p}{m} = \frac{m \, g \, t}{m} = g\, t[/math]

Für alle frei fallenden Körper gilt also:

[math] v = g\, t = 10\,\rm \frac{m}{s} \cdot t[/math]

Die Geschwindigkeit nimmt pro Sekunde um 10m/s zu!

• • den Aufprall auf der Wasseroberfläche.

Da der Mann mehr Impuls als die Frau hat, muss er auch stärker abgebremst werden, das heißt, die wirkende Kraft ist größer oder die Zeitdauer der Einwirkung ist größer. Wahrscheinlich wird beides der Fall sein: Der Mann spürt einen stärkerern Aufprall und taucht länger in das Wasser ein.

• Zeichne für beide die Geschwindigkeit-Zeit-, Impuls-Zeit- und Kraft-Zeit-Diagramme vor dem Aufprall.