Das Zentralfeld und die Abstandsgesetze (Gravitationsgesetz, Coulomb-Gesetz, magnetisches Coulomb-Gesetz): Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
Neigung:einen Meter lang, man misst die Höhe <math>x</math>. | Neigung:einen Meter lang, man misst die Höhe <math>x</math>. | ||
| − | Abstand <math>r</math> mit Schieblehre/Zollstock. | + | Abstand zwischen den Polen <math>r</math> mit Schieblehre/Zollstock. |
| + | |||
| + | Wo genau sind die Pole? Dazu kann man die Magnete in Eisenfeilspäne tauchen und schätzen. Sie sind ca. 5mm vom Rand des Magneten entfernt. Wir messen aber trotzdem erstmal den Abstand zwischen den Rändern des MAgneten und nicht zwischen den Polen. | ||
;Messwerte und Auswertung | ;Messwerte und Auswertung | ||
Die Kraft zwischen den Magneten berechnet sich als Hangabtriebskraft des Wagens: | Die Kraft zwischen den Magneten berechnet sich als Hangabtriebskraft des Wagens: | ||
:<math>F = m \, g \sin \alpha = m\, g \frac{x}{l}</math> | :<math>F = m \, g \sin \alpha = m\, g \frac{x}{l}</math> | ||
| − | r (cm) x (cm) F (N) | + | r'(cm) x (cm) F (N) |
0.49 51.8 0.5076 | 0.49 51.8 0.5076 | ||
0.55 47.2 0.4626 | 0.55 47.2 0.4626 | ||
| Zeile 41: | Zeile 43: | ||
Zur genaueren Untersuchung trägt man den Kehrwert der Wurzel von F über den Abstand r auf. Dabei sollte dann eine Gerade mit der Steigung <math>\frac{1}{\sqrt a}</math> zu sehen sein: | Zur genaueren Untersuchung trägt man den Kehrwert der Wurzel von F über den Abstand r auf. Dabei sollte dann eine Gerade mit der Steigung <math>\frac{1}{\sqrt a}</math> zu sehen sein: | ||
:<math>F = \frac{a}{r^2} \quad \Leftrightarrow \quad \sqrt F = \frac{\sqrt a}{r} \quad \Leftrightarrow \quad \frac{1}{\sqrt F} = \frac{1}{\sqrt a}\, r</math> | :<math>F = \frac{a}{r^2} \quad \Leftrightarrow \quad \sqrt F = \frac{\sqrt a}{r} \quad \Leftrightarrow \quad \frac{1}{\sqrt F} = \frac{1}{\sqrt a}\, r</math> | ||
| + | |||
| + | [[Datei:Auswertung_Coulombgesetz_magnetisch_1_durch_Wurzel_F_über_r.png|342px]] | ||
| + | |||
| + | Die Werte steigen tatsächlich einigermaßen linear an. Aber die Ausgleichsgerade geht nicht durch den Ursprung, sie ist nach links, bzw. nach oben verschoben. Wie kann man das interpretieren? | ||
| + | |||
| + | Addiert man zu den gemessenen Abständen noch 6,7mm dazu, dann verschiebt sich die Gerade genau in den Ursprung. Das liegt wohl daran, dass die magnetischen Ladungen nicht genau auf den Grenzflächen des Magneten sind, sondern etwas innerhalb liegen. Die magnetischen Ladungen "sitzen" ca. 3,4mm von der Oberfläche entfernt. | ||
| + | |||
| + | Im Folgenden versteht man daher unter dem Abstand r den Abstand der Pole. Das ist 6,7mm weniger als der Abstand r' der Magnete. Für den Zusammenhang zwischen F und r ergibt sich: | ||
| + | |||
| + | :<math>\frac{1}{\sqrt F} = 1071 r \quad \Leftrightarrow \quad \frac{1}{F^2} = 1070^2 r^2</math> | ||
| + | |||
| + | |||
| + | |||
Version vom 28. April 2014, 17:16 Uhr
Messung des magnetischen Abstandsgesetzes
Gilt [math]F \sim \frac{1}{r^2}[/math]?
- Aufbau
Schiefe Ebene, Je stärker die Neigung, desto näher sind die beiden Wagen.
Neigung:einen Meter lang, man misst die Höhe [math]x[/math].
Abstand zwischen den Polen [math]r[/math] mit Schieblehre/Zollstock.
Wo genau sind die Pole? Dazu kann man die Magnete in Eisenfeilspäne tauchen und schätzen. Sie sind ca. 5mm vom Rand des Magneten entfernt. Wir messen aber trotzdem erstmal den Abstand zwischen den Rändern des MAgneten und nicht zwischen den Polen.
- Messwerte und Auswertung
Die Kraft zwischen den Magneten berechnet sich als Hangabtriebskraft des Wagens:
- [math]F = m \, g \sin \alpha = m\, g \frac{x}{l}[/math]
r'(cm) x (cm) F (N) 0.49 51.8 0.5076 0.55 47.2 0.4626 0.70 44.0 0.4312 0.78 39.5 0.3871 0.90 35.4 0.3469 1.00 31.8 0.3116 1.12 27.8 0.2724 1.2 24.4 0.2391 1.4 20.5 0.2009 1.6 17.6 0.1725 1.9 14.3 0.1401 2.3 11.5 0.1127 2.5 10.0 0.0980 2.7 8.3 0.0813 3.2 6.4 0.0627 3.6 4.9 0.0480 4.7 3.2 0.0314 6.5 1.6 0.0157
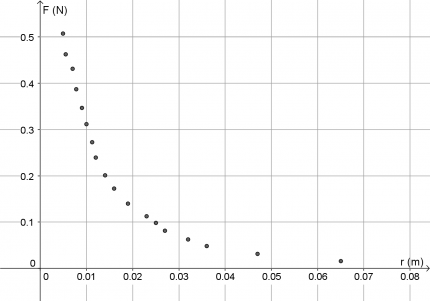
Zur Auswertung kann man erstmal die Kraft über den Abstand auftragen:
Das sieht schonmal ganz gut aus. Jetzt sollte bei einer Abstandsverdopplung sich die Kraft auf ein Viertel reduzieren. Von 0,5cm auf 1cm stimmt das nicht ganz und von 1cm auf 2cm auch nicht.
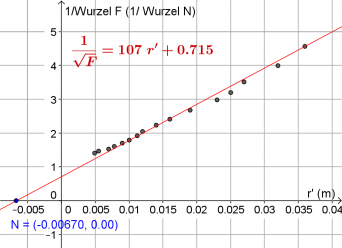
Zur genaueren Untersuchung trägt man den Kehrwert der Wurzel von F über den Abstand r auf. Dabei sollte dann eine Gerade mit der Steigung [math]\frac{1}{\sqrt a}[/math] zu sehen sein:
- [math]F = \frac{a}{r^2} \quad \Leftrightarrow \quad \sqrt F = \frac{\sqrt a}{r} \quad \Leftrightarrow \quad \frac{1}{\sqrt F} = \frac{1}{\sqrt a}\, r[/math]
Die Werte steigen tatsächlich einigermaßen linear an. Aber die Ausgleichsgerade geht nicht durch den Ursprung, sie ist nach links, bzw. nach oben verschoben. Wie kann man das interpretieren?
Addiert man zu den gemessenen Abständen noch 6,7mm dazu, dann verschiebt sich die Gerade genau in den Ursprung. Das liegt wohl daran, dass die magnetischen Ladungen nicht genau auf den Grenzflächen des Magneten sind, sondern etwas innerhalb liegen. Die magnetischen Ladungen "sitzen" ca. 3,4mm von der Oberfläche entfernt.
Im Folgenden versteht man daher unter dem Abstand r den Abstand der Pole. Das ist 6,7mm weniger als der Abstand r' der Magnete. Für den Zusammenhang zwischen F und r ergibt sich:
- [math]\frac{1}{\sqrt F} = 1071 r \quad \Leftrightarrow \quad \frac{1}{F^2} = 1070^2 r^2[/math]