Aufgaben zur Geschwindigkeit als Vektor - Lösungen: Unterschied zwischen den Versionen
(→3) Über den Atlantik fliegen) |
(→3) Über den Atlantik fliegen) |
||
| Zeile 46: | Zeile 46: | ||
====3) Über den Atlantik fliegen==== | ====3) Über den Atlantik fliegen==== | ||
| − | '''a)''' Von Frankfurt nach Los Angeles fliegt die Boeing mit einer Geschwindigkeit von nur | + | '''a)''' Von Frankfurt nach Los Angeles fliegt die Boeing mit einer Geschwindigkeit von nur 825 km/h relativ zum Erdboden. Damit benötigt sie für diese Strecke: |
:<math>v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{825\,\rm km/h} = \mathrm{11{,}27\, h = 11\, h\ 16\,min }</math> | :<math>v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{825\,\rm km/h} = \mathrm{11{,}27\, h = 11\, h\ 16\,min }</math> | ||
| Zeile 52: | Zeile 52: | ||
:<math>v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{1025\,\rm km/h} = \mathrm{9{,}07\, h = 11\, h\ 4\,min }</math> | :<math>v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{1025\,\rm km/h} = \mathrm{9{,}07\, h = 11\, h\ 4\,min }</math> | ||
| + | [[Datei:Aufgabe_Geschwindigkeit_vektoriell_Flugzeug.png|thumb|453px]] | ||
'''b)''' Bei Windstille beträgt die Entfernung hin und zurück 18600 km und die Geschwindigkeit beträgt 825 km/h: | '''b)''' Bei Windstille beträgt die Entfernung hin und zurück 18600 km und die Geschwindigkeit beträgt 825 km/h: | ||
:<math> \Delta t = \frac{\Delta s}{v} = \frac{18600\,\rm km}{825\,\rm km/h} = \mathrm{20{,}11\, h = 22\, h\ 6\,min }</math> | :<math> \Delta t = \frac{\Delta s}{v} = \frac{18600\,\rm km}{825\,\rm km/h} = \mathrm{20{,}11\, h = 22\, h\ 6\,min }</math> | ||
| Zeile 57: | Zeile 58: | ||
Das Flugzeug ist im Vergleich zum Hin- und Rückweg mit Westwind um 14 Minuten schneller! Und dass, obwohl man mit Rückenwind 100km/h schneller und mit Gegenwind 100km/h langsamer ist. <br/> Auf dem Hin- und Rückweg ist man aber eine längere Zeit mit Gegenwind als mit Rückenwind unterwegs. Deshalb kann der Rückenwind den Gegenwind nicht wieder "wettmachen". | Das Flugzeug ist im Vergleich zum Hin- und Rückweg mit Westwind um 14 Minuten schneller! Und dass, obwohl man mit Rückenwind 100km/h schneller und mit Gegenwind 100km/h langsamer ist. <br/> Auf dem Hin- und Rückweg ist man aber eine längere Zeit mit Gegenwind als mit Rückenwind unterwegs. Deshalb kann der Rückenwind den Gegenwind nicht wieder "wettmachen". | ||
| − | '''c)''' | + | '''c)''' Zuerst kann man ausrechnen, wie schnell das Flugzeug bei Windstille sein muss: |
| − | + | :<math>v = \frac{\Delta s}{\Delta t} = \frac{9300\,\rm km}{11,17\,\rm h} = 833\,\rm km/h</math> | |
| − | :<math>v | + | Gegen den Wind muss die Boing also mit 933 km/h relativ zur Luft fliegen und mit Rückenwind nur mit 733 km/h. |
| − | + | ||
| − | + | ||
Version vom 17. Oktober 2014, 17:54 Uhr
1) Eine Rolltreppe
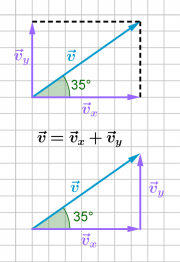
a) Die horizontale und die vertikale Geschwindigkeitskomponente stehen senkrecht aufeinander. Sie bilden mit dem Geschwindigkeitsvektor ein rechtwinkliges Dreieck. Für die Komponenten gilt daher:
- [math]\cos 35^\circ = \frac{v_x}{v}[/math]
- [math]\sin 35^\circ = \frac{v_y}{v}[/math]
Woraus folgt:
- [math]v_x = \cos 35^\circ \cdot v = 0{,}82 \cdot 80\,\rm \frac{cm}{s} = 66\,\rm \frac{cm}{s}[/math]
- [math]v_y = \sin 35^\circ \cdot v = 0{,}57 \cdot 80\,\rm \frac{cm}{s} = 46\,\rm \frac{cm}{s}[/math]
b) Alexander steigt in der Sekunde um 66 cm an, also braucht er 23s um die 15 Höhenmeter zu überwinden:
- [math]v_x = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad 0{,}66\,\rm \frac{m}{s} = \frac{15\,\rm m}{\Delta t}[/math]
Nach der Zeit aufgelöst:
- [math]\Delta t = \frac{15\,\rm m}{0{,}66\,\rm \frac{m}{s}} = 22{,}7\,\rm s[/math]
Oder man berechnet den schrägen Weg, also die Länge der Rolltreppe, den er mit 80cm/s zurücklegt.
2) Über den Fluss
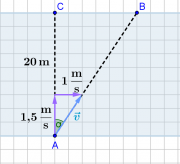
Wenn Eva senkrecht zur Wasserströmung paddelt, setzt sich ihre Geschwindigkeit relativ zum Ufer aus zwei zueinander senkrecht stehenden Komponenten zusammen.
a) Mit dem Satz des Pythagoras ergibt sich ihre Geschwindigkeit zu:
- [math]v^2 = \left( 1\,\rm \frac{m}{s}\right)^2 + \left( 1{,}5\,\rm\frac{m}{s} \right)^2 =[/math]
- [math]v= \sqrt{\left( 1\,\rm \frac{m}{s}\right)^2 + \left( 1{,}5\,\rm\frac{m}{s} \right)^2} = \sqrt{3{,}25\,\rm\frac{m^2}{s^2}} = 1{,}8 \,\rm\frac{m}{s}[/math]
b) Evas Geschwindigkeit quer zur Wasserströmung beträgt 1,5m/s. Daher braucht sie ca. 13s für die 20m bis zum anderen Ufer:
- [math]v_y = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad 1{,}5\,\rm \frac{m}{s} = \frac{20\,\rm m}{\Delta t}[/math]
Nach der Zeit aufgelöst ergibt sich:
- [math]\Delta t = \frac{20\,\rm m}{1{,}5\,\rm \frac{m}{s}} = 13{,}3\,\rm s[/math]
c) Da sie 13,3s unterwegs ist und in jeder Sekunde 1m abgetrieben wird, wird sie insgesamt um 13,3m abgetrieben:
- [math]v_x = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad 1\,\rm \frac{m}{s} = \frac{\Delta s}{13{,}3\,\rm s}[/math]
Nach der Strecke aufgelöst ergibt sich:
- [math]\Delta s = v\, \Delta t = 1\,\rm \frac{m}{s} \cdot 13{,}3\,\rm s = 30\,\rm m[/math]
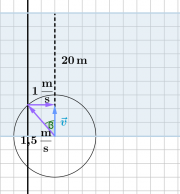
d) Eva muss so schräg fahren, dass die Summe ihrer Geschwindigkeit relativ zum Wasser und der Strömungsgeschwindigkeit senkrecht zur Wasserströmung ist. (Dazu muss ihre Geschwindigkeitskomponente gegen die Wasserströmung gerade 1m/s betragen.)
Daraus ergibt sich für den Winkel [math]\beta[/math]:
- [math]\sin \beta = \frac{1\,\rm \frac{m}{s}}{1{,}5\,\rm\frac{m}{s}} = 0{,}666[/math]
- [math]\beta =42^\circ[/math]
Eva muss also um 42° von dem direkten Kurs abweichen.
e) Um die Fahrtdauer zu bestimmen, muss man die Geschwindigkeit v kennen. Wieder hilft der Satz des Pythagoras:
- [math]\left(1{,}5\,\rm\frac{m}{s}\right)^2 = \left(1\,\rm\frac{m}{s}\right)^2 + v^2[/math]
Nach der Geschwindigkeit v auflösen:
- [math]v = \sqrt{\left(1{,}5\,\rm\frac{m}{s}\right)^2 - \left(1\,\rm\frac{m}{s}\right)^2} =\sqrt{1{,}25\,\rm\frac{m^2}{s^2}} \approx 1{,}12\,\rm\frac{m}{s} [/math]
Nun kann man die Zeit berechnen:
- [math]\Delta t = \frac{20\,\rm m}{1{,}12\,\rm \frac{m}{s}} = 18\,\rm s[/math]
Eva ist also 2s länger unterwegs als auf dem Hinweg.
3) Über den Atlantik fliegen
a) Von Frankfurt nach Los Angeles fliegt die Boeing mit einer Geschwindigkeit von nur 825 km/h relativ zum Erdboden. Damit benötigt sie für diese Strecke:
- [math]v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{825\,\rm km/h} = \mathrm{11{,}27\, h = 11\, h\ 16\,min }[/math]
Auf dem Rückweg fliegt sie mit 1025km/h. Damit benötigt sie für diese Strecke:
- [math]v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{1025\,\rm km/h} = \mathrm{9{,}07\, h = 11\, h\ 4\,min }[/math]
b) Bei Windstille beträgt die Entfernung hin und zurück 18600 km und die Geschwindigkeit beträgt 825 km/h:
- [math] \Delta t = \frac{\Delta s}{v} = \frac{18600\,\rm km}{825\,\rm km/h} = \mathrm{20{,}11\, h = 22\, h\ 6\,min }[/math]
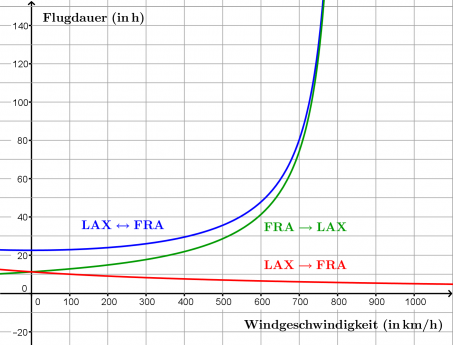
Das Flugzeug ist im Vergleich zum Hin- und Rückweg mit Westwind um 14 Minuten schneller! Und dass, obwohl man mit Rückenwind 100km/h schneller und mit Gegenwind 100km/h langsamer ist.
Auf dem Hin- und Rückweg ist man aber eine längere Zeit mit Gegenwind als mit Rückenwind unterwegs. Deshalb kann der Rückenwind den Gegenwind nicht wieder "wettmachen".
c) Zuerst kann man ausrechnen, wie schnell das Flugzeug bei Windstille sein muss:
- [math]v = \frac{\Delta s}{\Delta t} = \frac{9300\,\rm km}{11,17\,\rm h} = 833\,\rm km/h[/math]
Gegen den Wind muss die Boing also mit 933 km/h relativ zur Luft fliegen und mit Rückenwind nur mit 733 km/h.