Interferenz; Überlagerung von Wellen: Unterschied zwischen den Versionen
(→Versuch: Zwei Wasserkreiswellen) |
(→Beispiele) |
||
| Zeile 9: | Zeile 9: | ||
==Beispiele== | ==Beispiele== | ||
| − | <gallery widths=180px heights= | + | <gallery widths=180px heights=120px perrow=4 > |
Bild:Welle Interferenz Gespräch.jpg|<ref>Maryland GovPics http://commons.wikimedia.org/wiki/File:Dyskusja_przy_stole.jpg</ref> Was passiert, wenn die Schallwellen in der Mitte aufeinandertreffen? | Bild:Welle Interferenz Gespräch.jpg|<ref>Maryland GovPics http://commons.wikimedia.org/wiki/File:Dyskusja_przy_stole.jpg</ref> Was passiert, wenn die Schallwellen in der Mitte aufeinandertreffen? | ||
Bild:Regen_2.jpg|Wasserwellen durchdringen sich ungestört: [[Media:Wellenwanne_Tropfen.ogg|Video von fallenden Tropfen]] | Bild:Regen_2.jpg|Wasserwellen durchdringen sich ungestört: [[Media:Wellenwanne_Tropfen.ogg|Video von fallenden Tropfen]] | ||
Version vom 2. Januar 2016, 17:28 Uhr
(Kursstufe > Mechanische Wellen)
Wenn zwei Wellen an einem Ort aufeinandertreffen, so überlagern sie sich ungestört. Dieses Phänomen nennt man Interferenz. An jeder Stelle überlagern sich zwei Schwingungen, was man durch die Addition der zwei Auslenkungen, bzw. Zeiger beschreiben kann.
Je nach Frequenz und Phasenverschiebung können sich die Schwingungen aufheben oder verstärken. Dabei ändert sich die räumliche Energieverteilung.
Inhaltsverzeichnis
Beispiele
[1] Was passiert, wenn die Schallwellen in der Mitte aufeinandertreffen?
Wasserwellen durchdringen sich ungestört: Video von fallenden Tropfen
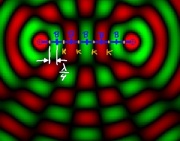
[2]Zur Schalldämpfung kann man einen Kopfhörer aufsetzen, indem ein "Gegenschall" gesendet wird.
Video: "Lärm" Wenn Töne weh tun, ab 1:00[3]Sonnenlicht ist eine Überlagerung aus elektromagnetischen Wellen von infrarotem Licht über das sichtbare bis zum ultravioletten.
Versuch: Das Interferenzrohr
- Aufbau
Ein Lautsprecher ist an einem Frequenzgenerator angeschlossen. Der Lautsprecher wird über einen Schlauch an ein Rohr angeschlossen, dass sich teilt und dann wieder zu einem Rohr vereint. Ähnlich wie bei einer Posaune kann man die eine Seite des Rohres verlängern. Am Ende befindet sich ein Hörschlauch, an den man sein Ohr hält.
Man stellt nun verschiedene Frequenzen ein (500 Hz, 1000 Hz, 2000 Hz) und verändert die Länge des einen Rohres, während man sich den Ton am Schlauch anhört. (Es genügt eine geringe Lautstärke!)
Statt mit dem eigenen Ohr kann man alternativ auch mit einem Mikrophon "lauschen" und das Ergebnis mit einem Oszilloskop darstellen.
- Beobachtung
Verlängert man ein Rohr, so verändert sich die Lautstärke des Tons rythmisch von laut zu leise und wieder laut, usw. Die Tonhöhe bleibt gleich. Sind beide Rohre gleichlang, so ist der Ton immer laut.
Je niedriger die Frequenz, desto mehr muss man das Rohr verlängern. In der Tabelle ist jeweils die gesamte Verlängerung angegeben:
| laut | leise | laut | leise | laut | |
| 500Hz | 0cm | 34cm | 68cm | ||
| 1000Hz | 0cm | 17cm | 34cm | 51cm | |
| 2000Hz | 0cm | 8cm | 17cm | 25cm | 34cm |
Zwei-Quellen-Interferenz
Versuch: Zwei Lautsprecher
- Aufbau
Man schließt zwei Lautsprecher parallel an einen Sinusgenerator. Alternativ kann man auch mit dem Computer und angeschlossenen Lautsprechern arbeiten.
(Tondateien: 110 Hz, 220 Hz, 440 Hz, 880 Hz)[4]
Danach läuft man im Raum herum und hört sich den Ton an.
Man wiederholt den Versuch mit verschiedenen Tonhöhen und, falls möglich, mit verschiedenen Abständen zwischen den Lautsprechern.
- Beobachtung
Beim Durchschreiten des Raumes hört man den Ton in unterschiedlichen Lautstärken, die einigermaßen rythmisch wechseln. Erhöht man die Frequenz (Tonhöhe) so liegen Orte mit geringer Lautstärke näher beisammen, verkleinert man den Abstand zwischen den Lautsprechern, so sind sie weiter auseinander.
Versuch: Zwei Wasserkreiswellen
- Aufbau
|
In einer Wellenwanne werden zwei Kreiswellen mit gleicher Frequenz erzeugt. Durch die Lichtbrechung an der unebenen Wasseroberfläche sieht man die Wellenfronten ("Berge und Täler") der Welle als helle und dunkle Streifen. |
- Beobachtung
- Video Zwei Steine in den Teich werfen (Youtube: Überlagerung und Interferenz zweier Kreiswellen von rastelli43)
- Eine ebene Welle trifft auf einen Doppelspalt
Erklärung
Wie kann es sein, dass die "Lautstärke" des einen Lautsprechers zusammen mit der anderen "Lautstärke" an manchen Orten nicht mehr, sondern weniger wird? Schließlich müßte dort ja auch doppelt soviel Energie vorhanden sein!
Die beiden (Kugel-) Wellen überlagern sich. An jedem Punkt des Raumes summieren sich zwei Schwingungen zu einer Gesamtschwingung, was sich durch die Addition der beiden Amplituden (bzw. der Zeiger) beschreiben läßt.
Je nach Überlagerungssituation wächst oder sinkt die Amplitude, der Ton wird lauter oder leiser.
Treffen an einer Stelle immer zwei Berge oder zwei Täler aufeinander, so verdoppelt sich dort die Amplitude. Das nennt man konstruktive Interferenz. Die Zeiger zeigen in die gleiche Richtung, es gibt keine Phasenverschiebung.
Trifft ein Berg auf ein Tal oder ein Tal auf einen Berg, so ist die Summe der Amplitude Null. Das nennt man destruktive Interferenz. Die Zeiger zeigen in entgegengesetzte Richtungen. Die Phasenverschiebung beträgt dann [math]\Pi[/math] oder 180°.
Animationen
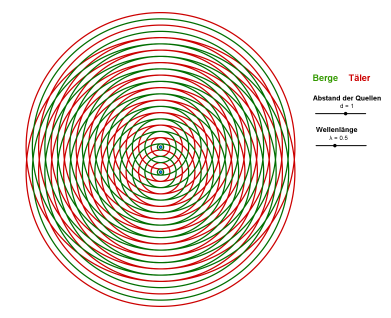
- Legt man zwei Folien mit konzentrischen Kreisen aufeinander ergibt sich ein ähnlicher, sogenannter "Moiré-Effekt". Man kann so gut nachvollziehen wo die Stellen mit konstruktiver oder destruktiver Interferenz liegen. Bei dieser Animation kann man das auch online tun.
- Die hellen Streifen, bei denen sich nur grüne mit grünen und rote mit roten Kreisen schneiden, sind Stellen mit konstruktiver Interferenz. Hier ist es laut.
- Die hellen Streifen, bei denen sich immer ein roter mit einem grünen Kreis schneidet sind die Stellen destruktiver Interferenz. Hier ist es leise.
- Mit Hilfe dieses Applets von Walter Fendt kann man ebenso die räumliche Verteilung der konstruktiven und destruktiven Interferenzen untersuchen. Da hier sich die Wellen auch bewegen, sieht man auch die Ausbreitungsrichtung.
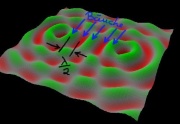
- Noch besser ist diese Simulation einer Wellenwanne von Paul Falstad. Stellt man "zwei Quellen mit einer Frequenz" ein, so kann man sehr gut den räumlichen und zeitlichen Verlauf der Überlagerung erkennen.
- Hier kann man auch gut die stehende Welle zwischen den Quellen beobachten. Dort befinden sich abwechselnd Stellen mit destruktiver und konstruktiver Interferenz.
- Ähnlich ist die Simulation von Wasser-, Schall-, und Lichtwellen der University of Colorado at Boulder. Dort kann man aber auch noch Messungen vornehmen.
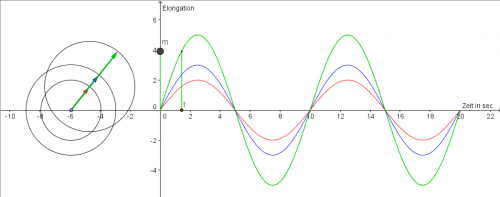
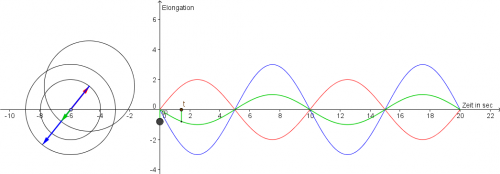
Animation der Zeigeraddition
Die Zeigeraddition kann man sich auch mit dieser Animation verdeutlichen. Zur Vereinfachung wird die Abnahme der Intensität von der Quelle nicht berücksichtigt. Die Länge der roten und blauen Zeiger sind immer gleich.
Die Stelle, an der man sich die Überlagerung zeigen lassen will, ist verschiebbar. (Wenn die drehenden Zeiger zu sehr nerven ist "Pause" eine gute Idee.)
- Untersuche zunächst die Überlagerung an verschiedenen Orten. Auch zwischen den Quellen.
- Wo findet man destruktive und wo konstruktive Interferenz?
- Lasse dir die Maxima und Minima anzeigen.
- Verändere nun den Abstand d der Quellen. Beschreibe die Veränderungen.
- Verändere nun die Wellenlänge und beschreibe was passiert.
- Auch mit diesem Applet von Peter Kraus kann man die Zeigeraddition gut verstehen. Um Zwei Quellen zu haben muss man "Doppelspalt" einstellen.
Ergebnis
Durch die Überlagerung zweier Wellen ist die Intensität der resultierenden Welle nicht mehr gleichmäßig über die Wellenfront verteilt. An manche Orte wird mehr Energie transportiert als an andere.
An jeder Stelle im Raum überlagern sich zwei Schwingungen mit gleicher Frequenz aber unterschiedlicher Phase.
Zur Berechnung der Amplitude an einer Stelle kann man die beiden Zeiger addieren.
Bei der Herleitung der Wellengleichung hat man gesehen, dass die Phase eines Zeigers von der Zeit und von der Entfernung zur Quelle abhängt:
- [math]\varphi_1=\omega \, t - \frac{2\pi}{\lambda}\, s_1[/math]
Der Phasenunterschied zwischen den Zeigern hängt nur vom Unterschied der Entfernungen zu den Quellen ab, dem Gangunterschied [math]\triangle s = s_2 - s_1[/math]:
- [math]\triangle \varphi= \frac{2\pi}{\lambda}\, \triangle s \qquad \Leftrightarrow \qquad \frac{\triangle \varphi}{2\pi}= \frac{\triangle s }{\lambda}[/math]
Sind die Schwingungen in Phase, so ergibt sich der längste Zeiger (die maximale Amplitude). Man spricht von konstruktiver Interferenz:
- [math]\triangle s = n \lambda \qquad \triangle \varphi = n 2 \pi \qquad (n= 0,1,2,3,...)[/math]
Den kürzesten Zeiger (die kleinste Amplitude) erhält man, wenn die beiden Zeiger in entgegengesetzte Richtungen zeigen. Man spricht von destruktiver Interferenz:
- [math]\triangle s = n \lambda - \lambda / 2 \qquad \triangle \varphi = n 2 \pi -\pi \qquad (n= 1,2,3,...)[/math]
Durch die Abnahme der Intensität mit der Entfernung von der Quelle verändern sich auch die Amplituden. Nur an Orten, bei denen der Gangunterschied Null beträgt sind die beiden Amplituden gleich. Oft wird dieser Effekt aber der Einfachheit halber vernachlässigt und man nimmt an, dass die Amplituden gleichgroß sind.
Links
- wikipedia: Interferenz
- Videos von Wassertropfen und Wasserwellen (Fachinformationszentrum Chemie, Berlin)
- Ein Applet, das eine Wellenwanne simuliert. Beeindruckend! (Von Paul Falstad.)
Quincke-Interferenzrohr
- Versuchsaufbau mit Mikrophon und Oszilloskop (LEIFI-Physik)
- Wikipedia: Quinckesches Interferenzrohr
Zwei Quellen
- Video Zwei Steine in den Teich werfen (Youtube: Überlagerung und Interferenz zweier Kreiswellen von rastelli43)
- Applet mit Interferenz zweier Kreis- oder Kugelwellen (Walter Fendt)
- Doppelspaltsimulation von Peter Kraus (pk-applets.de)
- Animation der Interferenz von Schall-, Wasser- oder Lichtwellen ("Interactive Simulations" der University of Colorado at Boulder)
- Zwei Quellen Interferenz (LEIFI)
- The Original Double Slit Experiment Ein einfacher Doppeltspalt-Versuch mit Licht in einer Kiste. Schönes Video zweier Wasserkreiswellen. (youtube: veritaserum)
Stehende Welle
- Applet LEIFI Überlagerung zweier gegenläufiger Wellen mit "Luftdruck"
- Applet der Überlagerung zweier gegenläufiger Wellenzüge zu einer stehenden Welle (Peter Kraus, pk-applets)
Gegenschall
- Zum Glück noch auf youtube: Video Planet Wissen - "Lärm" Wenn Töne weh tun - 1.4 WDR (Ab 1:00 min)
- Leider nur noch als Textvon der ARD: Video: Gegenschall als Lärmschutz( - W wie Wissen - ARD youtube channel)
Fußnoten
- ↑ Maryland GovPics http://commons.wikimedia.org/wiki/File:Dyskusja_przy_stole.jpg
- ↑ Gamer112 http://en.wikipedia.org/wiki/User:Gamer112
- ↑ commons: cuchulain
- ↑ Die Dateien wurden mit Audacity, einem freien Audioeditor und -rekorder erstellt.