Aufgaben zu Wellen (Kurs 2017): Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „('''Kursstufe''' > '''Mechanische Wellen''') ==Aufgaben== ===Grundlagen=== * 1) Was sind die typ…“)
(kein Unterschied)

Version vom 28. Januar 2016, 11:59 Uhr

(Kursstufe > Mechanische Wellen)

Aufgaben

Grundlagen

  • 1) Was sind die typischen Eigenschaften einer Welle?
  • 2) Erklären Sie die folgenden Begriffe anhand einer La Ola Welle in einem Stadion:
    • Transversal/Longitudinalwelle
    • Phasengeschwindigkeit
    • Wellenzug/lineare Welle
    • Amplitude
    • Frequenz
    • Wellenlänge
  • 3) Geben Sie Beispiele für Longitudinal- und Transversalwellen an und erklären Sie den Unterschied.
  • 4) Machen Sie anhand der La Ola Welle in einem Stadion klar, dass die Ausbreitungsgeschwindigkeit von der Kopplungsstärke der Schwinger, aber nicht von der Frequenz oder der Amplitude abhängt.
  • 5) Warum sind Longitudinalwellen in der Regel schneller als Transversalwellen?
  • 7) Wie kommt es dazu, dass bei einem Erbeben nach der ersten Erschütterungswelle noch eine zweite hinterherkommt?
  • 8) Geben Sie je ein Beispiel für eine Kugel- und eine Kreiswelle an.
  • 10) Geben Sie Beipsiele für Wellen an, die näherungsweise Zylinder- oder ebene Wellen sind. (Wieso nur näherungsweise?)
  • 12) Wie hängen Erregerfrequenz, Phasengeschwindigkeit und Wellenlänge zusammen?
  • 13) Wie groß sind die Wellenlängen der Schallwellen innerhalb des menschlichen Hörbereichs? (Wie verändern sich die Wellenlängen für Schallwellen im Wasser?)


Zeigermodell / Wellengleichung

  • 1) Nachdem eine Schwingung innerhalb von 3 Sekunden 6 ganze Schwingungen ausgeführt hat, hat sich diese Störung um 1,8 m ausgebreitet.
a) Bestimmen Sie Frequenz, Wellenlänge und Ausbreitungsgeschwindigkeit der Welle.
b) Wie groß ist der Phasenunterschied zweier Schwingungen im Abstand von 3m und 33m?
  • 3) Stellen Sie die Wellengleichung von Aufgabe 1) auf.
  • 4) Eine Transversalwelle hat die Wellenfunktion [math]y(x,t)= 2\,{\rm cm} \, \sin(\frac{2}{\rm s} \cdot t -\frac{5}{\rm cm} \cdot x)[/math].
a) Zeichnen Sie die Welle zum Zeitpunkt t=0, also zu Beginn der Zeitrechnung, und 0,32 Sekunden später in ein Koordinatensystem. (Mit dem GTR ist das ganz einfach!)
b) Bestimmen Sie Amplitude, Frequenz und Wellenlänge.

Reflektion

  • 1) Wie wird ein Wellenberg am festen und wie am losen Ende reflektiert? Geben Sie jeweils ein reales Beispiel für eine solche Situation an.


Interferenz

Zwei Lautsprecher
  • 1) Woran kann man im Alltag erkennen, dass sich Wellen störungsfrei überlagern?
  • 2) Beschreiben Sie den Versuch mit den zwei Lautsprechern, die an einem Sinusgenerator angeschlossen sind.
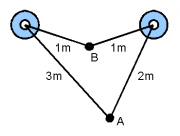
  • 3) Die beiden Lautsprecher sind 1,5 m voneinander entfernt und schwingen in Phase mit einer Frequenz von 858 Hz.
a) Bestimmen Sie die Lautstärke an den Punkten A und B mit Hilfe eines Zeigerdiagramms. Vernachlässigen Sie dabei die Abnahme der Schallintensität durch den größeren Abstand vom Lautsprecher und der Dämpfung.
b) Suchen Sie zwei Stellen zwischen den Lautsprechern, bei denen der Ton besonders leise bzw. besonders laut ist.
c) Wie verändert sich qualitativ die Situation in den Punkten A und B, wenn man die Änderung der Schallintensität nicht vernachlässigt?
d) Bestimmen Sie die exakte Schwingungsgleichung für die Punkte A und B, wenn beide Lautsprecher mit einem Watt senden.

Beugung

Blick auf einen kleinen Hafen
  • 1) Erklären Sie an einem Alltagsphänomen die Beugung von Wellen.
  • 2) Warum haben Stereoanlagen zwei Boxen aber nur einen "Subwoofer", den man auch unter das Sofa stellen kann, was man aber besser mit den Boxen nicht tut?
  • 3) Hinter einer Lärmschutzwand ist der Verkehrslärm auch ohne Sichtkontakt zur Strasse noch zu hören. Der Verkehr klingt dumpfer als beim direkten Hinhören. Erklären Sie die Beobachtungen.
  • 4) Erklären Sie das Foto der Wellen an einem Hafen.

Brechung

  • 1) Nennen Sie ein Alltagsphänomen, bei dem Brechung auftritt.
  • 2) Erklären Sie das Phänomen der Brechung mit Hilfe des Huygenschen Prinzips.
a) Zeichnen Sie den Übergang einer Welle von einem Medium in ein anderes mit nur halber Ausbreitungsgeschwindigkeit bei einem Einfallswinkel von 60°.
b) Leiten Sie das Brechungsgesetz her.

Stehende Wellen

Die Pfeife im Querschnitt
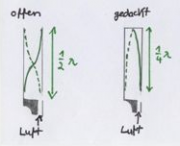
  • 1) Bestimmen Sie die Höhe des Grundtones und des ersten Obertones der Orgelpfeife im offenen und gedackten Fall, wenn die Pfeife einen halben Meter lang ist.

Lösungen

Von „http://schulphysikwiki.de/index.php?title=Aufgaben_zu_Wellen_(Kurs_2017)&oldid=10875“