Die Bewegungsmenge: Impuls und Drehimpuls: Unterschied zwischen den Versionen
(→Beispiele) |
K (→Beispiele) |
||
| Zeile 11: | Zeile 11: | ||
</gallery> | </gallery> | ||
| − | *Verschiedene Bälle, am besten gleich groß aber mit unterschiedlichen Massen, fangen und werfen. (Oder "Kegeln", denn dabei spielt die Gewichtskraft keine Rolle. Oder "Dosenwerfen" mit | + | *Verschiedene Bälle, am besten gleich groß aber mit unterschiedlichen Massen, fangen und werfen. (Oder "Kegeln", denn dabei spielt die Gewichtskraft keine Rolle. Oder "Dosenwerfen" mit verschiedenen Bällen.) |
*Ein sich schnell drehendes Fahrrad-Rad kann man nicht so ohne weiteres anschubsen, abbremsen oder kippen. Es "wehrt sich". | *Ein sich schnell drehendes Fahrrad-Rad kann man nicht so ohne weiteres anschubsen, abbremsen oder kippen. Es "wehrt sich". | ||
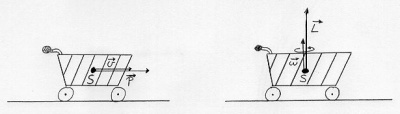
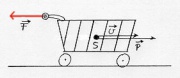
* Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht. | * Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht. | ||
Version vom 9. April 2017, 22:42 Uhr
Inhaltsverzeichnis
Beispiele
[1]Beim Curling muss man dem Stein den richtigen Schwung mitgeben,
- Verschiedene Bälle, am besten gleich groß aber mit unterschiedlichen Massen, fangen und werfen. (Oder "Kegeln", denn dabei spielt die Gewichtskraft keine Rolle. Oder "Dosenwerfen" mit verschiedenen Bällen.)
- Ein sich schnell drehendes Fahrrad-Rad kann man nicht so ohne weiteres anschubsen, abbremsen oder kippen. Es "wehrt sich".
- Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht.
Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn.
(Dreh-)Impuls als Bewegungsmenge
- Die Bewegung eines Körpers kann man als eine Überlagerung einer Translation im Raum und eine Drehung in sich beschreiben.
- Die Bewegung wird durch die Menge an Impuls [math]\vec p[/math](Schwung) für die Translation und Drehimpuls [math]\vec L[/math] (Drehschwung) für die Rotation angegeben.
- Sowohl Impuls als auch Drehimpuls haben eine Richtung und sind vektorielle Größen. Sie geben an, wieviel Schwung, bzw. Drehschwung ein Gegenstand hat, also wieviel "Bewegungsmenge" in dem Körper steckt. Außerdem gibt er an in welche Richtung er sich bewegt, bzw. um welche Achse er sich dreht.
- In der Schulphysik betrachtet man in der Regel Bewegungen von Gegenständen, bei denen die Drehbewegung keine Rolle spielt und beschreibt nur die Translation.
Definition des (Dreh-)Impulses
- Ein Ball enthält viel Impuls, wenn er schnell ist und er eine große Masse hat. Man legt den Impuls daher als Produkt der beiden Größen fest.
- Leider hat die Einheit des Impulses keinen allgemeingültigen eigenen Namen bekommen, im Karlsruher Physikkurs wird sie nach Christiaan Huygens (1629–1695) benannt.
Impuls- und Geschwindigkeitsvektor sind parallel,
die Masse ist der Proportionalitätsfaktor:- [math]\vec p = m \vec v[/math]
- [math][\vec p\,] = \mathrm{1kg \frac{1m}{1s} = 1Hy}[/math] (lies: Huygens)
- Ein Rad enthält viel Drehimpuls, wenn es schnell rotiert und eine große Masse möglichst weit entfernt von der Drehachse hat.
- Die Trägheit gegenüber Drehungen, sozusagen die "Drehmasse", gibt das Trägheitsmoment des Gegenstandes an.
- Video von herabrollender Dose und Zylinder.
- Video der Drehschwingung eines Menschen auf einem Drehstuhl.
Drehimpulsvektor und Winkelgeschwindigkeit sind ebenfalls parallel,
Proportionalitätsfaktor ist das Trägheitsmoment[2]:- [math]\vec L = \Theta \, \vec \omega[/math]
Das Wasserbehältermodell
Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.)
- Mit welcher Masse und welcher Geschwindigkeit enthält das Auto einen Impuls von 10 Hy?
Trägheitsgesetz (1. Newtonsches Axiom)
Mit Hilfe des Impulses kann man das Trägheitsgesetz genauer fassen:
|
Jeder Gegenstand behält ohne Wechselwirkung mit einem anderen Körper
|
Veränderungsgesetz (2. Newtonsches Axiom)
|
Drückt (zieht) man mit einer Kraft [math]\vec F[/math] an einem Gegenstand,
Dreht man mit einem Drehmoment [math]\vec M[/math] ("Drehkraft") an einem Gegenstand,
|
Aufgaben
- 1) Berechne jeweils die Impulsmenge
- a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h.
- b) Ein Fußgänger (m=72 kg) läuft mit 5 km/h.
- c) Ein Auto (m=1 t) fährt mit 36 km/h.
- 2) Anke und ihr Papa fahren zusammen Rad.
- Anke wiegt 40 kg, ihr Vater 90 kg, jedes ihrer Räder 10kg. Sie fahren mit 18 km/h nebeneinander.
- a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern?
- Stelle dies mit dem Wasserbehältermodell dar.
- b) Wie schnell muss Anke fahren, um genausoviel Impuls wie ihr Vater zu haben? (mit Rädern)
- Stelle auch dies im Wasserbehältermodell dar.
- 3) Ball und Gewehrkugel
- Ein Ball (m=6,24 kg) kann bei einer Geschwindigkeit von 10 km/h einen Holzklotz umschmeißen.
- Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat?
Lösungen
Links
- Video von herabrollender Dose und Zylinder. (Fakultät für Physik Uni Wien; eLearning)
- Video der Drehschwingung eines Menschen auf einem Drehstuhl. (youtube: "Trägheitsmomente" von "Wissenschaftskanal1")
Fußnoten
- ↑ Bild von Ralf Roletschek, CC by SA 3.0
- ↑ Das gilt eigentlich nur für Achsen, bezüglich der Körper keine Unwucht hat, der sogenannten "Hauptträgheitsachsen". Für Drehachsen, die auch eine Symmetrieachse des Körpers sind, hat der Körper keine Unwucht. Ist im Abstand r von der Achse die Masse m verteilt, so beträgt das Trägheitsmoment [math]\Theta = m\ r^2[/math].