Praktikum: Einen Kondensator laden und entladen (Auswertung): Unterschied zwischen den Versionen
(→Die Energiemenge) |
(→Die Energiemenge) |
||
| Zeile 48: | Zeile 48: | ||
Dieser Kondensator ist daher kein besonders effizienter Energiespeicher. Von der hineingesteckten Energie geht 2/3 "verloren". | Dieser Kondensator ist daher kein besonders effizienter Energiespeicher. Von der hineingesteckten Energie geht 2/3 "verloren". | ||
| + | |||
| + | Ein idealer Kondensator verhält sich dagegen wie eine elastische Stahlfeder, bei dem die Kraft proportional zur Auslenkung ist und keine Energieverluste auftreten. | ||
==Links== | ==Links== | ||
*Wikipedia: [https://de.wikipedia.org/wiki/Hysterese Hysterese] | *Wikipedia: [https://de.wikipedia.org/wiki/Hysterese Hysterese] | ||
*[http://www.oocities.org/rubbermuseum/german/page0420.htm Physik des Gummis] von "RubberHans" | *[http://www.oocities.org/rubbermuseum/german/page0420.htm Physik des Gummis] von "RubberHans" | ||
Version vom 10. Mai 2017, 14:57 Uhr
Inhaltsverzeichnis
Erstellen der Diagramme
Zur besseren Erfassung der Messwerte wurde der Ladevorgang und der Entladevorgang gefilmt. Mit dem Programm "avidemux" kann man dann bequem den Film vor- und zurückspulen. (Das Video des Ladevorgangs und das Video des Entladevorgangs)
Der Stromstärke und Spannungsverlauf wurde in eine Tabellenkalkulation eingegeben. (LibreOffice-Calc-Datei)
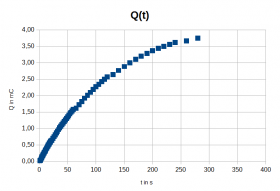
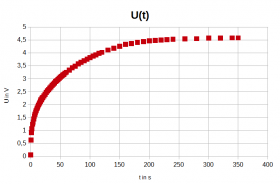
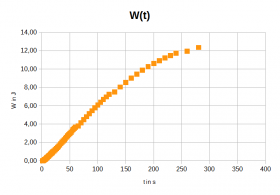
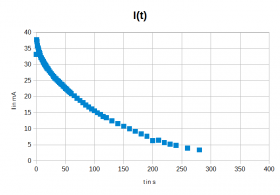
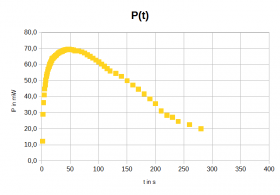
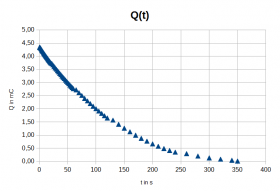
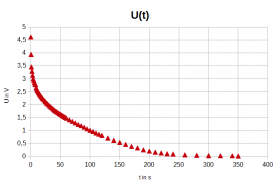
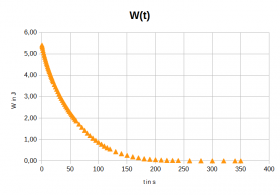
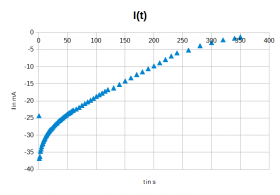
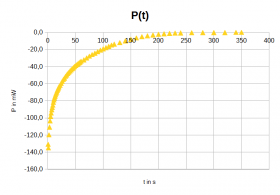
- Diagramme des Ladevorgangs
Der Verlauf der Ladungskurve entspricht beschränktem Wachstum.
Auch die Spannung nähert sich exponentiell einer oberen Schranke.
Die gespeicherte Energie nimmt zunächst linear zu, dann nähert sie sich einer oberen Schranke.
Die Stromstärke fällt ungefähr exponentiell ab.
Die Kennlinie dieses Kondensators ist nicht linear!
Die Leistung erreicht nach ca. einer Minute ein Maximum und fällt dann ab.
.png)
.png)
.png)
.png)
.png)
.png)
- Diagramme des Entladevorgangs
Die Ladung nähert sich exponentiell einer oberen Schranke.
Die Spannung fällt zunächst stark ab, danach fällt sie ungefähr exponentiell.
Die gespeicherte Energie nimmt exponentiell ab.
Die Stromstärke ist negativ, weil sich die Stromrichtung ändert. Der Betrag der Stromstärke fällt zunächst stark ab, dann sinkt er fast linear.
Auch beim Entladen ergibt sich keine lineare Kennlinie.
Die Leistung ist negativ, weil die Energiemenge abnimmt. Der Betrag der Leistung fällt exponentiell.
.png)
.png)
.png)
.png)
.png)
.png)
Die Kapazität
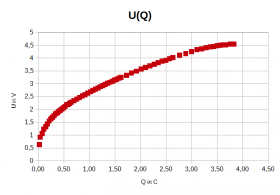
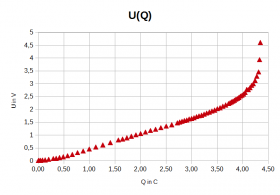
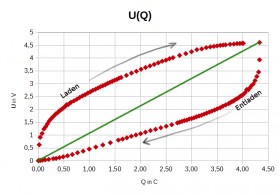
Die Kennlinie dieses Kondensators ist nicht linear. Sowohl beim Laden als auch beim Entladen sind die Spannung und die Ladung nicht zueinander proportional. Es macht daher eigentlich keinen Sinn, dem Kondensator eine Kapazität zuzuordnen.
_mit_idealer_Kennlinie.png) |
Während des Ladens benötigt man 0,5C Ladung, um eine Spannung von 2V zu erreichen, was einer Kapazität von 0,25F entspricht und mit 2,5C geflossener Ladung steigt die Spannung auf 4V, was einer Kapazität von 0,6F entspricht. Während des Entladens sind bei 4V Spannung 4,3C Ladung gespeichert, was einer Kapazität von 1,1F entspricht und bei 1V Spannung sind es 2C Ladung, was der Kapazität 2F entspricht. Auf dem Kondensator steht trotzdem die Angabe: "5.5V / 1F". Dies ist eine grobe lineare Näherung. |
Die Energiemenge
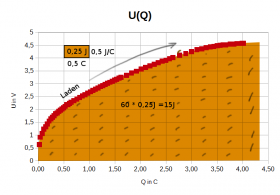
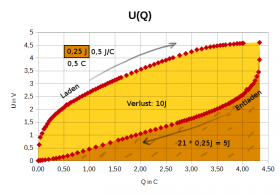
Die in den Kondensator hinein oder herausgeflossene Energie kann man mit der Fläche im U(Q)-Diagramm berechnen.
Man zählt etwa 60 Kästchen à 0,25 Joule, insgesamt fließen also ca. 15 Joule Energie in den Kondensator hinein.
Die Fläche unter der Entladekurve ist viel kleiner. Nur noch 5 Joule Energie können beim Entladen genutzt werden. Der Energie-"Verlust" beträgt 10 Joule.
_mit_Bemerkungen.png)
_mit_Energie.png)
Der Kondensator verhält sich wie ein Luftballon. Beim Aufblasen benötigt man einen großen Druckunterschied, um Luft hineinzubekommen, denn das Gummi ist fest. Beim Herauslassen der Luft ist das Gummi schlapper und der Druckunterschied dementsprechend geringer. Auch beim Luftballon geht also Energie "verloren". Misst man das Verhalten von Gummi an einem Gummiband, so erhält man ähnliche Kennlinien.
Dieses Verhalten nennt man "Hysterese", es tritt bei vielen Veränderungen auf, die nur mit Energie"verlust" wieder rückgängig gemacht werden können.
Dieser Kondensator ist daher kein besonders effizienter Energiespeicher. Von der hineingesteckten Energie geht 2/3 "verloren".
Ein idealer Kondensator verhält sich dagegen wie eine elastische Stahlfeder, bei dem die Kraft proportional zur Auslenkung ist und keine Energieverluste auftreten.
Links
- Wikipedia: Hysterese
- Physik des Gummis von "RubberHans"
