*: Unterschied zwischen den Versionen

Version vom 20. November 2017, 11:24 Uhr (Quelltext anzeigen) Patrick.Nordmann (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 23. November 2017, 14:28 Uhr (Quelltext anzeigen) Patrick.Nordmann (Diskussion | Beiträge) Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
	__NOTOC__		__NOTOC__
−	==Praktikum: Wovon hängt die Frequenz des frei schwingenden Pendels ab?==	+	===Noch mehr Aufgaben zur Interferenz von Licht===
−	[[Datei:Praktikum Fadenpendel Aufbau.jpg|thumb|]]	+	=====6) Lichtfarben und Wellenlänge=====
−	* Untersuchen Sie experimentell, wovon die Frequenz, bzw. die Schwingungsdauer eines Pendels abhängt.	+	:Ein Gitter wird vom Licht einer Glühlampe beleuchtet. Hinter dem Gitter ist im Abstand von 60cm ein Schirm. ([[Optische_Gitter#Versuch:_Gl.C3.BChlampenlicht_trifft_auf_ein_Gitter|Versuchsaufbau]]) Hier die Ergebnisse:
−	* Als vereinfachtes Modell der Schaukel oder des Uhrenpendels nehmen wir einen an einem Faden hängenden Gegenstand. Wir nehmen an, dass die Ausdehnung des Gegenstandes klein ist gegenüber der Fadenlänge. In der Vereinfachung ist die Masse in einem Punkt, dem Schwerpunkt, konzentriert und der Faden masselos. Die Pendellänge ist dann der Abstand vom Aufhängepunkt zum Schwerpunkt. Eine solche Abstraktion heißt auch "mathematisches Pendel".	+	<gallery widths=180px heights=130px  perrow=3 >
		+	Bild:Gitter_Messung_80pro_mm_60cm_Spalt_schmal.jpg|Gitter mit 80 Linien pro mm
		+	Bild:Gitter_Messung_300pro_mm_60cm.jpg|Gitter mit 300 Linien pro mm
		+	</gallery>
−	Mögliche Beeinflussungen durch:	+	'''a)''' Bestimmen Sie aus den Messergebnissen die Wellenlänge von violettem, blauen, grünem, gelben und rotem Licht. Vergleichen Sie Ihre Ergebnisse mit Literaturwerten.
−	* Pendellänge l	+	'''b)''' Warum ist das Maximum nullter Ordnung weiss und nicht bunt wie die anderen?
−	* Masse <math>m</math>	+
−	* Amplitude  <math>\hat y</math>	+
−	* Reibung	+
−	* Antrieb	+
−	Man darf immer nur eine Größe variieren und dann jeweils die Periode messen. Misst man z.B. für verschiedene Amplituden die Periode erhält man einen Zusammenhang zwischen Amplitude und Periodendauer, der streng genommen nur für die gewählte Länge, Masse usw. gilt.	+
−	<br>Ändert sich die Periode bei Variation einer Größe nicht, so ist sie davon unabhängig.	+
−	Den Zusammenhang zwischen der Periodendauer und der Reibung bzw. des Antriebs kann man mit diesem Versuchsaufbau nicht untersuchen.	+	'''c)''' Zu dem Gitter mit 80 Linien pro mm:
		+	*Warum ist das zweite Maximum breiter als das erste?
		+	*Begründen Sie, dass das zweite Maximum doppelt so breit sein müsste wie das erste. Wie breit ist demnach das dritte?
−	;Aufbau:	+	=====7) Einzelspalt=====
−	[[Bild:Fadenpendel_Versuchsaufbau.jpg|thumb|right|Das Fadenpendel]]	+	Beleuchtet man einen schmalen Spalt mit weißem Licht, so kann man dahinter ein buntes Streifenmuster auf einem Schirm beobachten.
		+	*Wie kommt es zu den wiederholten dunklen Stellen? Fertigen Sie eine Zeichnung zur Begründung an.
		+	*Wie kommt es zu den farbigen Rändern der hellen Stellen?
		+	:Sind die hellen Stellen nach Außen hin oder zur Mitte hin rot? Begründen Sie.
−	Mittels einer Klemme wird eine Stange senkrecht an einem Tisch angebracht. An dieser Stange wird am oberen Ende eine kleine Querstange befestigt und an dieser eine Klemme.	+	Ein Einzelspalt hat eine Breite von genau einer Wellenlänge des einfallenden Lichtes.
		+	*Wie breit ist das nullte Maximum, oder genauer: Unter welchem Winkel ist das Maximum nullter Ordnung zu sehen?
−	Mit der Klemme wird nun ein Faden befestigt, an dessen Ende ein kleines Gewicht hängt.	+	=====8) Haaresbreite=====
		+	:'''a)''' Bestimmen Sie mit aus den Messergebnissen des "[[Doppelspaltversuch_(Schatten_eines_Haares)#Versuch:_Der_Schatten_eines_Haares|Haarschattenversuchs]]" die Wellenlänge des Laserlichts.
		+	:'''b)''' Mit einem Laserpointer läßt man rotes Licht der Wellenlänge 650nm auf ein Haar fallen. Die Dicke des Haares hat man vorher zu 5 Hundertstel mm gemessen. Auf der 2m entfernten Wand kann man nun eine interessante Beobachtung machen.
		+	:Zeichnen Sie das auf der Wand sichtbare Muster in Originalgröße.
−	*Zur Untersuchung der Abhängigkeit von einer Größe muß diese variiert und alle anderen konstant gehalten werden.	+	=====9) Ein Seidenschal=====
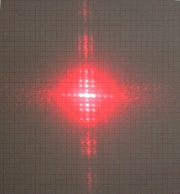
		+	:Ein roter Laserpointer, mit einer Wellenlänge von 630nm  wird auf einen Schal gerichtet. Drei Meter hinter dem Schal kann man folgende Beobachtung machen:
		+	:[[Datei:Licht_Interferenz_Schal_3m.jpg|none|thumb]]
		+	*Erklären Sie die Beobachtung. Welche Eigenschaften des Schals können Sie daraus berechnen?
		+	*Oder genauer: Bestimmen Sie die Dicke der Fäden und die Breite der Lücken in horizontaler und vertikaler Richtung.
−	;Beobachtung/Messwerte:	+	=====10) Eine CD oder DVD=====
		+	:Ein Laserpointer emmittiert Licht einer Wellenlänge von 630nm und wird auf eine CD gerichtet. Man macht folgende Beobachtung:
		+	:[[Datei:Lichtinterferenz_CD_Reflektionsgitter_Beobachtung.jpg|thumb|none]]
		+	:Zwischen den Maxima Nullter und erster Ordnung bildet sich ein Winkel von 22°.
		+	*Berechnen Sie daraus den Abstand zwischen den Rillen einer CD und schätzen Sie daraus die Anzahl der Rillen der CD ab.
		+	:Wie groß ist der Winkel zum Maximum zweiter Ordnung?
		+	*Erkundigen Sie sich nach dem Rillenabstand einer DVD.
		+	:Wie verändert sich das Interferenzmuster, wenn man die CD durch eine DVD austauscht?
−	*Abhängigkeit von der Pendellänge l:	+	=====11) Mehrfachspalt und Zeigeraddition=====
−	:Die Pendellängen sollen ca. folgende Werte haben: 0,05m 0,1m 0,2m 0,3m 0,4m 0,5m.	+	[[Datei:RCL_Vierfachspalt_532nm_10um_40um.jpg|thumb]]
−		+	Das nebenstehende Bild zeigt das Bild eines Schirms hinter einem beleuchteten Mehrfachspalt. Der verwendete Laser hat eine Wellenlänge von 532nm und der Abstand zwischen Spalt und Schirm beträgt 1m.
−	Masse <math>m \rm \text{ in } kg</math>:	+	*Wieviele Spalte hat der Mehrfachspalt? Begründen Sie in Worten und mit Hilfe von Zeigeraddition.
−		+	*Wie breit sind die einzelnen Spalte und wie groß ist der Mittenabstand zwischen den Spalten?
−	Amplitude <math>\hat y  \rm \text{ in } ^{\circ} </math>:	+
−		+
−	{| class="wikitable"	+
−	|-	+
−	||<math>l  \rm \text{ in } m</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:80px;" |	+
−	|-	+
−	|<math>10 \, T \rm \text{ in } s</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math>T \rm \text{ in } s</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math> \frac{T}{l} \text{ in } {\rm \frac{s}{m} }</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math> \frac{T}{l^2} \text{ in } {\rm \frac{s}{m^2} }</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math> \frac{T}{\sqrt{l}} \text{ in } {\rm \frac{s}{\sqrt{m}} }</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|}	+
−		+
−	*Abhängigkeit von der Masse m:	+
−	:Durch Anhängen eines zweiten Gewichts kann man die Masse verdoppeln oder man verwendet verschiedene Gegenstände.	+
−		+
−	Pendellänge <math>l \rm \text{ in } m</math>:	+
−		+
−	Amplitude <math>\hat y \rm \text{ in } ^{\circ} </math>:	+
−		+
−	{| class="wikitable"	+
−	|-	+
−	| <math>m  \rm \text{ in } kg</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:80px;" |	+
−	|-	+
−	|<math>10 \, T \rm \text{ in } s</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math>T \rm \text{ in } s</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|}	+
−		+
−	*Abhängigkeit von der Amplitude <math>\hat y</math>:	+
−		+
−	Masse <math>m \rm \text{ in } kg</math>:	+
−		+
−	Pendellänge <math>l  \rm \text{ in } m</math>:	+
−		+
−	{| class="wikitable"	+
−	|-	+
−	|<math>\hat y \rm \text{ in } ^{\circ} </math>	+
−	| style="height:30px; width:80px;" |  5°	+
−	| style="height:30px; width:80px;" |  10°	+
−	| style="height:30px; width:80px;" |  20°	+
−	| style="height:30px; width:80px;" |  40°	+
−	| style="height:30px; width:80px;" |  60°	+
−	| style="height:30px; width:80px;" |  80°	+
−	|-	+
−	|<math>10 \, T \rm \text{ in } s</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math>T \rm \text{ in } s</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math> \frac{T}{\hat y} \text{ in } {\rm \frac{s}{\circ} }</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math> \frac{T}{\hat y^2} \text{ in } {\rm \frac{s}{\circ ^2} }</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|-	+
−	|<math> \frac{T}{\sqrt{\hat y}} \text{ in } {\rm \frac{s}{\sqrt{\circ}} }</math>	+
−	| style="height:30px; width:80px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	| style="height:30px; width:50px;" |	+
−	|}	+
−		+
−	;Erklärung/Auswertung:	+
−		+
−	Die gemessenen Zusammenhänge werden jeweils in ein Koordinatensystem gezeichnet. Man trägt zum Beispiel die Periodendauer (y-Achse) über die halbe Stangenlänge (x-Achse) auf.	+
−		+
−	Um einen rechnerischen Zusammenhang zwischen den Größen zu finden, sucht man nach konstanten Quotienten oder Produkten der Messgrößen. Diese werden in die Tabelle eingetragen.	+
−		+
−	Als Beispiel hier der Zusammenhang zwischen Periodendauer und Pendellänge. Es kommen mehrere Möglichkeiten in Betracht:	+
−	#<math>T = c \cdot l \quad \Leftrightarrow \quad c = \frac{T}{l}</math>	+
−	#<math>T = c \cdot l^2 \quad \Leftrightarrow \quad c = \frac{T}{l^2}</math>	+
−	#<math>T = c \cdot \sqrt{l} \quad \Leftrightarrow \quad c = \frac{T}{\sqrt{l}}</math>	+
−		+
−	Man berechnet daher alle Quotienten und untersucht, ob ein Quotient für alle Messungen ungefähr gleich bleibt. Wenn dies der Fall ist, so nimmt man den Mittelwert der Quotienten, um damit eine Formel aufzustellen.	+

---

Version vom 23. November 2017, 14:28 Uhr

Noch mehr Aufgaben zur Interferenz von Licht

6) Lichtfarben und Wellenlänge

Ein Gitter wird vom Licht einer Glühlampe beleuchtet. Hinter dem Gitter ist im Abstand von 60cm ein Schirm. (Versuchsaufbau) Hier die Ergebnisse:

• 

  Gitter mit 80 Linien pro mm

• 

  Gitter mit 300 Linien pro mm

a) Bestimmen Sie aus den Messergebnissen die Wellenlänge von violettem, blauen, grünem, gelben und rotem Licht. Vergleichen Sie Ihre Ergebnisse mit Literaturwerten.

b) Warum ist das Maximum nullter Ordnung weiss und nicht bunt wie die anderen?

c) Zu dem Gitter mit 80 Linien pro mm:

• Warum ist das zweite Maximum breiter als das erste?
• Begründen Sie, dass das zweite Maximum doppelt so breit sein müsste wie das erste. Wie breit ist demnach das dritte?

7) Einzelspalt

Beleuchtet man einen schmalen Spalt mit weißem Licht, so kann man dahinter ein buntes Streifenmuster auf einem Schirm beobachten.

• Wie kommt es zu den wiederholten dunklen Stellen? Fertigen Sie eine Zeichnung zur Begründung an.
• Wie kommt es zu den farbigen Rändern der hellen Stellen?

Sind die hellen Stellen nach Außen hin oder zur Mitte hin rot? Begründen Sie.

Ein Einzelspalt hat eine Breite von genau einer Wellenlänge des einfallenden Lichtes.

• Wie breit ist das nullte Maximum, oder genauer: Unter welchem Winkel ist das Maximum nullter Ordnung zu sehen?

8) Haaresbreite

a) Bestimmen Sie mit aus den Messergebnissen des "Haarschattenversuchs" die Wellenlänge des Laserlichts.

b) Mit einem Laserpointer läßt man rotes Licht der Wellenlänge 650nm auf ein Haar fallen. Die Dicke des Haares hat man vorher zu 5 Hundertstel mm gemessen. Auf der 2m entfernten Wand kann man nun eine interessante Beobachtung machen.

Zeichnen Sie das auf der Wand sichtbare Muster in Originalgröße.

9) Ein Seidenschal

Ein roter Laserpointer, mit einer Wellenlänge von 630nm wird auf einen Schal gerichtet. Drei Meter hinter dem Schal kann man folgende Beobachtung machen:

• Erklären Sie die Beobachtung. Welche Eigenschaften des Schals können Sie daraus berechnen?
• Oder genauer: Bestimmen Sie die Dicke der Fäden und die Breite der Lücken in horizontaler und vertikaler Richtung.

10) Eine CD oder DVD

Ein Laserpointer emmittiert Licht einer Wellenlänge von 630nm und wird auf eine CD gerichtet. Man macht folgende Beobachtung:

Zwischen den Maxima Nullter und erster Ordnung bildet sich ein Winkel von 22°.

• Berechnen Sie daraus den Abstand zwischen den Rillen einer CD und schätzen Sie daraus die Anzahl der Rillen der CD ab.

Wie groß ist der Winkel zum Maximum zweiter Ordnung?

• Erkundigen Sie sich nach dem Rillenabstand einer DVD.

Wie verändert sich das Interferenzmuster, wenn man die CD durch eine DVD austauscht?

11) Mehrfachspalt und Zeigeraddition

Das nebenstehende Bild zeigt das Bild eines Schirms hinter einem beleuchteten Mehrfachspalt. Der verwendete Laser hat eine Wellenlänge von 532nm und der Abstand zwischen Spalt und Schirm beträgt 1m.

• Wieviele Spalte hat der Mehrfachspalt? Begründen Sie in Worten und mit Hilfe von Zeigeraddition.
• Wie breit sind die einzelnen Spalte und wie groß ist der Mittenabstand zwischen den Spalten?