Aufgaben zur Gravitation: Masse und Gewichtskraft (Lösungen): Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
'''1) Massen messen''' | '''1) Massen messen''' | ||
| − | Im Unterricht haben wir die Masse | + | Im Unterricht haben wir die Masse einer Packung Couscous gemessen. |
| − | *Wir haben | + | *Wir haben das Couscous auf eine Balkenwaage gelegt. In die andere Waagschale haben wir Gewichtstücke gelegt, bis die Waage im Gleichgewicht war. Das Couscous hatte eine Masse von 520 Gramm. |
Mein Fahrrad hat eine Masse von ca. 12 Kilogramm. | Mein Fahrrad hat eine Masse von ca. 12 Kilogramm. | ||
| Zeile 27: | Zeile 27: | ||
:*[https://www.youtube.com/watch?v=n4bpGTrcPoQ Sendung mit der Maus - Wie entstehen Ebbe und Flut] | :*[https://www.youtube.com/watch?v=n4bpGTrcPoQ Sendung mit der Maus - Wie entstehen Ebbe und Flut] | ||
:*[http://www.youtube.com/watch?v=TuVsCsieCVA Wissen vor 8: Wie kommt es zu Ebbe und Flut] | :*[http://www.youtube.com/watch?v=TuVsCsieCVA Wissen vor 8: Wie kommt es zu Ebbe und Flut] | ||
| − | + | *Die Flutwelle kommt aus dem Westen und wird an der Nordseeküste aufgestaut. Dort gibt es große Unterschiede zwischen Ebbe und Flut. | |
| + | :Die Ostsee hat fast keine Verbindung zum Atlantik. So kann die Flutwelle nicht "hineinschwappen" und es entsteht nur ein geringer Unterschied zwischen Ebbe und Flut. | ||
==Gewichtskraft und Ortsfaktor== | ==Gewichtskraft und Ortsfaktor== | ||
| Zeile 52: | Zeile 53: | ||
'''2) ein Schulranzen''' | '''2) ein Schulranzen''' | ||
| − | + | [[Datei:Merkregel_Dreisatz_Fmg.png|thumb]] | |
Ein Schulranzen wird mit einer Kraft von 36N zur Erde gezogen. | Ein Schulranzen wird mit einer Kraft von 36N zur Erde gezogen. | ||
*Welche Masse hat der Ranzen? | *Welche Masse hat der Ranzen? | ||
| + | :Wenn man mit einem Ortsfaktor von <math>10\,\rm\frac{N}{kg}</math> rechnet, wird jedes Kilogramm Masse mit 10 Newton angezogen. Also hat der Ranzen eine Masse von 3,6kg. | ||
| + | :Das kann man auch mit einer Formel berechnen: | ||
| + | ::<math>m=\frac{F_G}{g}= \frac{36\,\rm N}{10\,\rm\frac{N}{kg}}= 3{,}6\,\rm kg</math> | ||
'''3) auf dem Mond II''' | '''3) auf dem Mond II''' | ||
| Zeile 60: | Zeile 64: | ||
Auf den Mond hat man verschiedene Gegenstände von der Erde mitgenommen. Bereits auf der Erde hat man die Massen dieser Gegenstände mit einer Balkenwaage bestimmt. Mit einem Federkraftmesser messen die Astronauten nun auf dem Mond, wie stark die Gegenstände vom Mond angezogen werden. | Auf den Mond hat man verschiedene Gegenstände von der Erde mitgenommen. Bereits auf der Erde hat man die Massen dieser Gegenstände mit einer Balkenwaage bestimmt. Mit einem Federkraftmesser messen die Astronauten nun auf dem Mond, wie stark die Gegenstände vom Mond angezogen werden. | ||
:'''a)''' Warum müssen die Astronauten die Massen der Gegenstände auf dem Mond nicht noch einmal messen? | :'''a)''' Warum müssen die Astronauten die Massen der Gegenstände auf dem Mond nicht noch einmal messen? | ||
| + | :Die Masse ist auf dem Mond die gleiche wie auf der Erde! | ||
:'''b)''' Trage die Messergebnisse in ein Koordinatensystem ein. Falls du schon ein Koordinatensystem mit Messwerten auf der Erde hast, dann trage sie dort ein! (x-Achse: Masse <math>m</math> in <math>\rm kg</math> , y-Achse: Gewichtskraft <math>F_G</math> in <math>\rm N</math>.) | :'''b)''' Trage die Messergebnisse in ein Koordinatensystem ein. Falls du schon ein Koordinatensystem mit Messwerten auf der Erde hast, dann trage sie dort ein! (x-Achse: Masse <math>m</math> in <math>\rm kg</math> , y-Achse: Gewichtskraft <math>F_G</math> in <math>\rm N</math>.) | ||
:'''c)''' Ergänze in der Tabelle jeweils den Quotienten von Gewichtskraft <math>F_G</math> und Masse (in <math>\rm \frac{N}{kg}</math> ). Was stellst du fest? | :'''c)''' Ergänze in der Tabelle jeweils den Quotienten von Gewichtskraft <math>F_G</math> und Masse (in <math>\rm \frac{N}{kg}</math> ). Was stellst du fest? | ||
| Zeile 86: | Zeile 91: | ||
0,048 | 0,048 | ||
|valign="top"; style="border-style: solid; border-width: 4px "| | |valign="top"; style="border-style: solid; border-width: 4px "| | ||
| − | + | 1,6 | |
|- | |- | ||
|style="border-style: solid; border-width: 4px "| | |style="border-style: solid; border-width: 4px "| | ||
| Zeile 95: | Zeile 100: | ||
0,4 | 0,4 | ||
|valign="top"; style="border-style: solid; border-width: 4px "| | |valign="top"; style="border-style: solid; border-width: 4px "| | ||
| − | + | 1,6 | |
|- | |- | ||
|style="border-style: solid; border-width: 4px "| | |style="border-style: solid; border-width: 4px "| | ||
| Zeile 104: | Zeile 109: | ||
0,24 | 0,24 | ||
|valign="top"; style="border-style: solid; border-width: 4px "| | |valign="top"; style="border-style: solid; border-width: 4px "| | ||
| + | 1,6 | ||
|- | |- | ||
|style="border-style: solid; border-width: 4px "| | |style="border-style: solid; border-width: 4px "| | ||
| Zeile 112: | Zeile 118: | ||
0,16 | 0,16 | ||
|valign="top"; style="border-style: solid; border-width: 4px "| | |valign="top"; style="border-style: solid; border-width: 4px "| | ||
| + | 1,68 | ||
|- | |- | ||
|style="border-style: solid; border-width: 4px "| | |style="border-style: solid; border-width: 4px "| | ||
| Zeile 120: | Zeile 127: | ||
0,39 | 0,39 | ||
|valign="top"; style="border-style: solid; border-width: 4px "| | |valign="top"; style="border-style: solid; border-width: 4px "| | ||
| + | 1,63 | ||
|} | |} | ||
Version vom 7. Januar 2018, 22:55 Uhr
1) Massen messen
Im Unterricht haben wir die Masse einer Packung Couscous gemessen.
- Wir haben das Couscous auf eine Balkenwaage gelegt. In die andere Waagschale haben wir Gewichtstücke gelegt, bis die Waage im Gleichgewicht war. Das Couscous hatte eine Masse von 520 Gramm.
Mein Fahrrad hat eine Masse von ca. 12 Kilogramm.
- Auf der Welt gibt es genau ein Kilogramm. Es ist ein kleiner Metall-Zylinder und wird in Paris aufbewahrt. Von diesem sogenannten Standard-Kilogramm wurden viele Kopien für alle Länder auf der Erde hergestellt. Das deutsche Kilogramm wird in der Physikalisch Technischen Bundesanstalt in Braunschweig aufbewahrt.
- So kann jedes Land nachwiegen, was ein Kilogramm ist.
- Mein Fahrrad müsste also mit 12 Kopien des Standardkilogramms auf einer Balkenwaage im Gleichgewicht sein!
2) Gravitation
Wir erleben ständig, dass Dinge zu Boden fallen oder zum Boden hin gezogen werden.
- Alle Dinge ziehen sich gegenseitig an, das nennt man Massenanziehung oder Gravitation. Die Wirkung ist sehr klein und nur spürbar, wenn große Gegenstände mit viel Masse, wie die Erde, im Spiel sind.
- Was sich gegenseitig anzieht:
- Erde und Mond
- Sonne und Erde
- Erde und Apfel
- Buch und Schere :)
4) Ebbe und Flut
An der Nordsee kann man regelmäßig sehen, wie die Wasserhöhe sich ändert.
- Es gibt zweimal am Tag Ebbe und zweimal Flut, also alle 6 Stunden ein Wechsel.
- Zur Erklärung schaut man sich am besten diese Filme an:
- Die Flutwelle kommt aus dem Westen und wird an der Nordseeküste aufgestaut. Dort gibt es große Unterschiede zwischen Ebbe und Flut.
- Die Ostsee hat fast keine Verbindung zum Atlantik. So kann die Flutwelle nicht "hineinschwappen" und es entsteht nur ein geringer Unterschied zwischen Ebbe und Flut.
Gewichtskraft und Ortsfaktor
1) Gewichtskraft berechnen
- Mit welcher Gewichtskraft werden diese Gegenstände zur Erde gezogen?
- a) eine Tafel Schokolade b) ein Kilogramm Mehl c) 350 g Zucker d) du selbst!
Der Ortsfaktor auf der Erde beträgt:
- [math]g= 9{,}81\,\rm \frac{N}{kg}[/math]
Kennt man die Masse [math]m[/math] eines Gegenstandes, so kann man die Gewichtskraft [math]F_G[/math]mit dem Ortsfaktor berechnen:
- [math]F_G = m \cdot g = m \cdot 9{,}81\,\rm \frac{N}{kg}[/math]
Dabei ist es wichtig, die Masse in kg einzusetzen. Die Rechnung ergibt die Gewichtskraft in Newton.
- a) eine Tafel Schokolade: [math]F_G = 0{,}100\,\rm kg \cdot 9{,}81\,\rm \frac{N}{kg} = 0{,}981\,\rm N \approx 1\,\rm N[/math]
- b) ein Kilogramm Mehl: [math]F_G = 1 \,\rm kg \cdot 9{,}81\,\rm \frac{N}{kg} = 9{,}81\,\rm N \approx 10\,\rm N[/math]
- c) 350 g Zucker: [math]F_G = 0{,}350\,\rm kg \cdot 9{,}81\,\rm \frac{N}{kg} = 3{,}4335\,\rm N \approx 3{,}5\,\rm N[/math]
- d) ich selbst: [math]F_G = 80\,\rm kg \cdot 9{,}81\,\rm \frac{N}{kg} = 784{,}8\,\rm N \approx 800\,\rm N[/math]
|
Merkregel: Die Gewichtskraft einer Tafel Schokolade beträgt 1 Newton! |
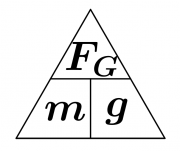
2) ein Schulranzen
Ein Schulranzen wird mit einer Kraft von 36N zur Erde gezogen.
- Welche Masse hat der Ranzen?
- Wenn man mit einem Ortsfaktor von [math]10\,\rm\frac{N}{kg}[/math] rechnet, wird jedes Kilogramm Masse mit 10 Newton angezogen. Also hat der Ranzen eine Masse von 3,6kg.
- Das kann man auch mit einer Formel berechnen:
- [math]m=\frac{F_G}{g}= \frac{36\,\rm N}{10\,\rm\frac{N}{kg}}= 3{,}6\,\rm kg[/math]
3) auf dem Mond II
Auf den Mond hat man verschiedene Gegenstände von der Erde mitgenommen. Bereits auf der Erde hat man die Massen dieser Gegenstände mit einer Balkenwaage bestimmt. Mit einem Federkraftmesser messen die Astronauten nun auf dem Mond, wie stark die Gegenstände vom Mond angezogen werden.
- a) Warum müssen die Astronauten die Massen der Gegenstände auf dem Mond nicht noch einmal messen?
- Die Masse ist auf dem Mond die gleiche wie auf der Erde!
- b) Trage die Messergebnisse in ein Koordinatensystem ein. Falls du schon ein Koordinatensystem mit Messwerten auf der Erde hast, dann trage sie dort ein! (x-Achse: Masse [math]m[/math] in [math]\rm kg[/math] , y-Achse: Gewichtskraft [math]F_G[/math] in [math]\rm N[/math].)
- c) Ergänze in der Tabelle jeweils den Quotienten von Gewichtskraft [math]F_G[/math] und Masse (in [math]\rm \frac{N}{kg}[/math] ). Was stellst du fest?
- d) Wie groß ist der Ortsfaktor auf dem Mond? Stelle eine Formel für die Gewichtskraft eines Gegenstandes auf dem Mond auf.
- e) Berechne die Gewichtskraft der Gegenstände von Aufgabe 1) auf dem Mond.
|
Gegenstand |
Masse [math]m[/math] (in [math]\rm kg[/math] ) |
Gewichtskraft [math]F_G[/math] (in [math]\rm N[/math] ) |
Gewichtskraft pro Masse [math]\frac{F_G}{m}[/math] (in [math]\rm \frac{N}{kg}[/math] ) |
|---|---|---|---|
|
Stift |
0,030 |
0,048 |
1,6 |
|
Hammer |
0,250 |
0,4 |
1,6 |
|
Handschuh |
0,150 |
0,24 |
1,6 |
|
Apfel |
0,095 |
0,16 |
1,68 |
|
Telefon |
0,240 |
0,39 |
1,63 |
5) Unsere Planeten
Auf den Planeten underes Sonnensystems gibt es gibt es unterschiedliche Ortsfaktoren.
|
Merkur |
[math]g=9{,}7\,\rm\frac{N}{kg}[/math] |
Mein |
|
Venus |
[math]g=8{,}87\,\rm\frac{N}{kg}[/math] |
Vater |
|
Erde |
[math]g=9{,}81\,\rm\frac{N}{kg}[/math] |
Erklärt |
|
Mars |
[math]g=3{,}69\,\rm\frac{N}{kg}[/math] |
Mir |
|
Jupiter |
[math]g=24{,}8\,\rm\frac{N}{kg}[/math] |
Jeden |
|
Saturn |
[math]g=10{,}4\,\rm\frac{N}{kg}[/math] |
Sonntag |
|
Uranus |
[math]g=8{,}9\,\rm\frac{N}{kg}[/math] |
Unsere |
|
Neptun |
[math]g=11{,}2\,\rm\frac{N}{kg}[/math] |
Nachbarplaneten |
- a) Wie kann man die Unterschiede zwischen den Planeten erklären?
- b) Berechne für alle Planeten die Gewichtskraft, mit der du dort angezogen wirst.