Das Konzept der Energie (Energieträger und Potential): Unterschied zwischen den Versionen
(→Systemisches Denken - Beschreibung eines Zustandes) |
(→Anwendungen des Wasserbehältermodells in Beispielen) |
||
| Zeile 140: | Zeile 140: | ||
:φ: chem. Potenzial μ | :φ: chem. Potenzial μ | ||
| − | :<math>I_E=I_n* | + | :<math>I_E=I_n*\mu</math> |
| − | :<math>\dot E=\dot n* | + | :<math>\dot E=\dot n*\mu</math> |
| − | + | Bei der Änderung der Schokoladenstoffmenge ändert sich das chemische Potenzial nicht. | |
| + | Dafür gilt hier: | ||
| + | |||
| + | <math>E=n*\mu</math> | ||
| + | |||
| + | *'''Kochplatte''' | ||
| + | |||
| + | :Träger: Entropie S | ||
| + | :Potenzial: Temperatur Tetta | ||
| + | <math>\dot E=\dot S*\tetta</math> | ||
| + | |||
| + | [[Bild:Kochplatten Modell.JPG|thumb|Kochplatte & Topf mit Wasser]] | ||
| + | In diesem Fall können die Temperaturen von Herdplatte und Topf sich zunächst verändern, nach einer längeren Zeit bleiben sie jedohc konstant. Für den konstanten Fall gilt wieder, dass pro Sekunde die Energiemenge <math>\dot E=\dot S*\delta (= Differnz der Temperaturen zwischen Herdplatte und Topf) tetta</math> übertragen wird. | ||
| + | |||
| + | *'''Stausee''' | ||
| + | |||
| + | [[Bild: Staudamm modell.JPG|thumb|Stausee]] | ||
| + | |||
| + | :T Schwerefeld, "m" | ||
| + | :\varphi: gh | ||
| + | <math>\dot E=\dot m * gh</math> | ||
| + | |||
| + | Fließt der Massestrom auf einer konstanten Höhe in den See, so fügt jede Masse m dem See die Energie m*gh zu. | ||
| + | |||
| + | Die Energie des gesamten Stausees beträgt: | ||
| + | <math>E=m*gh_S</math> | ||
Version vom 17. Oktober 2006, 20:01 Uhr
Inhaltsverzeichnis
Energie
- Energie ist das Geld der Physik. Man bewertet damit Situationen.
- Es ist alles andere als selbstverständlich, daß wirklich sämtliche Situationen vergleichbar und in einer Einheit auch bewertbar sind.
- Energie ist eine Erhaltungsgröße, sie kann weder erzeugt, noch vernichtet werden.
- In der Regel ist die absolute Energiemenge eines Körpers uninteressant. Man interessiert sich viel mehr für die Energiemengen, die hinaus oder hineingehen.
- Die Veränderungen der Energiemenge kann man durch einen Energiestrom beschreiben, bei dem gleichzeitig auch der Energieträger strömt.
- Es ist (leider!?) auch üblich der gespeicherten Energie einen anderen Namen zu geben als der Energie, welche strömt. Man nennt die gespeicherte Energie eine Zustandsgröße, die strömende eine Prozessgröße.
Zustandsgröße Prozessgröße Energie mechanische Arbeit thermische Energie Wärme
Energiemenge eines Wassergefüllten Glases
- Es gibt verschiedene Energieformen / Energieträger:
- thermische Energie/ Entropie
- Druckenergie / Wasser
- Lageenergie / Schwerefeld
- Bewegungsenergie / Impuls
- Einige Energien sind vom Bezugssystem abhängig:
- Lageenergie / Schwerefeld
- Bewegungsenergie / Impuls
Energie- und Energieträgerströme
Das Wasserbehältermodell
- Wassermenge und Stromstärke (Durchsatz)
- Wasserhöhe und Druck
- Widerstandskonzept:
- Druckunterschied als Antrieb
- Stömungswiderstand
- Energietransportkonzept:
- Druck als Energiebeladungsmaß
- Druckunterschied als Potentialdifferenz
- Energiestromgleichung (Leistung) [math]P=\triangle p I_W \qquad \qquad \dot E = \triangle p \dot W [/math]
Es gibt zwei Konzepte:
- Antrieb-Widerstand
- Energieträger & Potenzial
Das Wasserbehältermodell besteht aus zwei, mit unterschiedlich viel Wasser gefüllten, Zylindern. Sobald man die Drehverschlüsse an beiden Seiten aufgedreht, strömt das Wasser aus dem höher mit Wasser gefüllten Bottich in den Zweiten. Dieser Vorgang lässt sich mit Hilfe des Wasserrädchens beobachten und stoppt erst, nachdem die Wasserpegel beider Seiten sich auf ein gleiches Niveau begeben haben.
- a) Die Strömung entsteht durch den vonstatten gehenden Druckausgleich, der durch die unterschiedlichen Druckverhältnisse in den Gefäßen verursacht wird. Die Druckdifferenz zwischen dem Zylinder mit dem höheren und dem niedrigeren Wasserpegel, ist der Antrieb. Ein Widerstand besteht durch die Reibung in der Wasserleitung und dem Wasserrädchen, dadurch fließt das Wasser nur langsam in den anderen Behälter.
- b) Das Wasser ist der sogenannte Energieträger, der auf der Seite mit dem höheren Wasserpegel, auf Grund des höheren Drucks mit mehr Energie beladen ist. Sobald eine Verbindung zwischen den beiden Behältern gegeben ist, versuchen die unterschiedlichen Energiepegel (Potenziale) sich auf beiden Seiten auszugleichen. Ein Teil der Druckenergie wird „auf dem Weg“ zur anderen Seite zu Wärme umgewandelt, da die Reibung die sogenannte Reibungsenergie freisetzt.
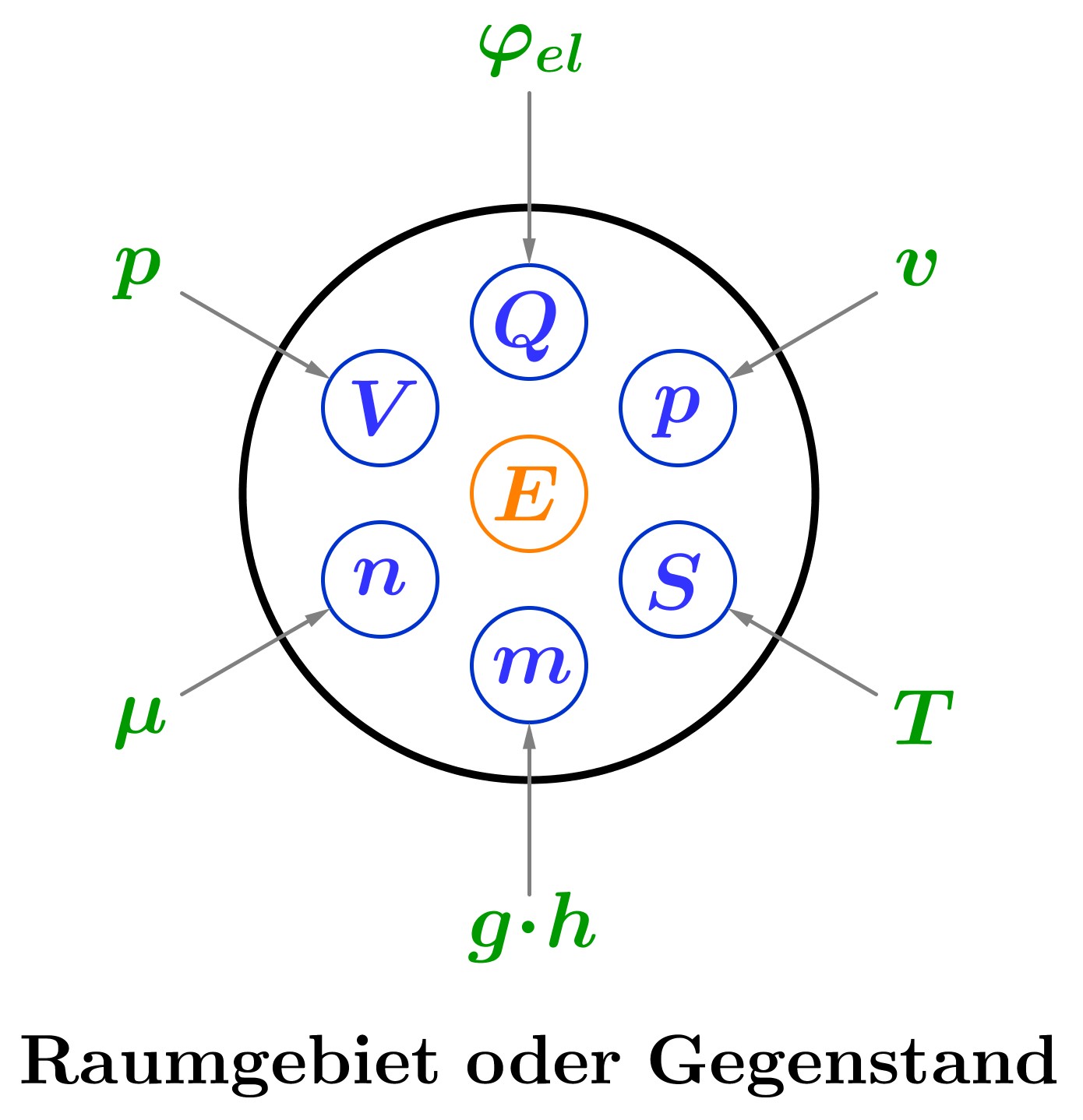
Systemisches Denken - Beschreibung eines Zustandes
E: Energiemenge [math][E]=\mathrm{J \quad(Joule)}[/math]
S: Entropiemenge [math][S] = \mathrm{Ct \quad (Carnot)}[/math]
V: Volumen [math][V] = \mathrm{m^3}[/math]
m: Masse [math][m] = \mathrm{kg}[/math]
p: Impuls [math][p] = \mathrm{Hy \quad (Huygens)= kg \frac{m}{s}} [/math]
Q: el. Ladung [math][Q] = \mathrm{C \quad (Coulomb)}[/math]
n: Stoffmenge [math][n] = \mathrm{mol}[/math]
Mengenartige (extensive) Größen
Hat zugehörige Eigenschaften (intensive Größen), welche man Potential nennt.
ν: Temperatur
p: Druck
gh: Schwerepotential
φel: el. Potential
μ: chem. Potential (freie molare Standardenthalpie)
Systemveränderungen
- Verändert sich die Energiemenge, so verändert sich auch immer noch eine andere mengenartige Größe, der sogenannte Enrgieträger!
- Der Energiestrom ist proportional zum Trägerstrom. Das Potential ist gerade die Proportionalitätskonstante.
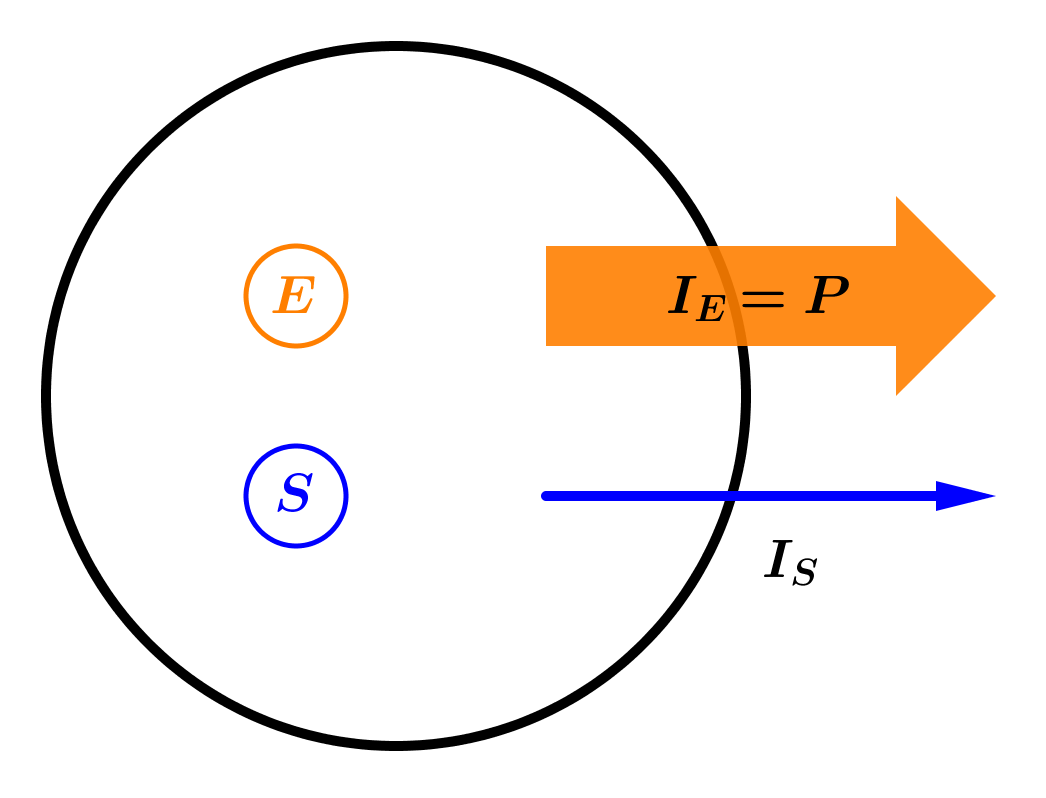
- Eine andere mathematische Schreibweise für die Stromstärke ist die momentane zeitliche Änderungsrate, also die Ableitung nach der Zeit. Die zeitliche Ableitung einer Größe notiert man mit einem Punkt über dem Symbol. Zum Beispiel gilt: [math]I_S = \dot S[/math]
- In der Regel strömt aber Stoff von einem Gebiet in ein Anderes. Sind die Potentiale unterschiedlich, gibt es einen Netto-Energiestrom von den beiden Systemen weg.
- Bsp.: Von dem warmen Wasser über das Thermoelement in das kalte Wasser fließt ein Entropiestrom. Es kommt weniger Energie an, als wegfließt, weil die Temperatur und damit die Beladung des Entropiestromes abnimmt. Die Energie ist auf die elektrische Ladung umgeladen worden, welche dann wiederum in der Lampe auf das Licht und Entropie geladen wird.
Datei:Energieströme.jpg P = Energetische Stromstärke/Energiestrom
Anwendungen des Wasserbehältermodells in Beispielen
- zusammengedrückte Körper: Stoffvolumen und Druck
- erwärmte Körper: Entropie und Temperatur
- Körper im Schwerefeld: Masse und „Höhe“ (Schwerepotential)
- Stromkreis: Ladungsmenge und el. Potential
- bewegte Körper: Impuls und Geschwindigkeit
- chemische Reaktion: Stoffmenge und „freie molare Standardenthalpie“
- Luftballon
- Trägergröße: Volumen
- Potenzial: Druck
- [math]I_E=I_v*p[/math]
- [math]\dot E= \dot V*p[/math]
- Wenn beim Druck [math]p[/math] der Luftballon um das Volumen [math]V[/math] kleiner wird, so verringert sich die enthaltene Energie um [math]E = V*p[/math]
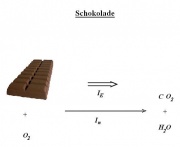
- Schokolade
- T: Stoffmenge
- φ: chem. Potenzial μ
- [math]I_E=I_n*\mu[/math]
- [math]\dot E=\dot n*\mu[/math]
Bei der Änderung der Schokoladenstoffmenge ändert sich das chemische Potenzial nicht. Dafür gilt hier:
[math]E=n*\mu[/math]
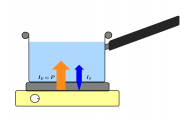
- Kochplatte
- Träger: Entropie S
- Potenzial: Temperatur Tetta
[math]\dot E=\dot S*\tetta[/math]
In diesem Fall können die Temperaturen von Herdplatte und Topf sich zunächst verändern, nach einer längeren Zeit bleiben sie jedohc konstant. Für den konstanten Fall gilt wieder, dass pro Sekunde die Energiemenge [math]\dot E=\dot S*\delta (= Differnz der Temperaturen zwischen Herdplatte und Topf) tetta[/math] übertragen wird.
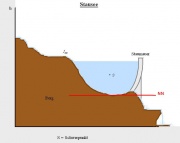
- Stausee
- T Schwerefeld, "m"
- \varphi: gh
[math]\dot E=\dot m * gh[/math]
Fließt der Massestrom auf einer konstanten Höhe in den See, so fügt jede Masse m dem See die Energie m*gh zu.
Die Energie des gesamten Stausees beträgt: [math]E=m*gh_S[/math]