|
|
| Zeile 1: |
Zeile 1: |
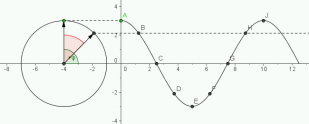
| | + | [[Bild:Welle_Phasenverschiebung.png|thumb|right|309px|Die Welle breitet sich nach rechts aus. Die Schwingungen B, C,... hinken dem linken Nachbar jeweils um <math>\Pi / 4</math>, also 45° hinterher. (Aus den [http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/wellen/welleinhalt.html dynamischen Arbeitsblättern zur Wellenlehre].)]] |
| | + | |
| | Im Falle einer räumlich unbegrenzten, linearen harmonischen Welle kann man die Welle relativ einfach beschreiben. In einer solchen Welle sind alle Schwingungen harmonisch und die Welle breitet sich nur längs einer Raumrichtung aus. Kugelwellen, Kreiswellen oder Zylinderwellen sind also keine solchen Wellen, ebene Wellen schon. Ausserdem werden räumlich begrenzte Wellenpakete ausgeschlossen. | | Im Falle einer räumlich unbegrenzten, linearen harmonischen Welle kann man die Welle relativ einfach beschreiben. In einer solchen Welle sind alle Schwingungen harmonisch und die Welle breitet sich nur längs einer Raumrichtung aus. Kugelwellen, Kreiswellen oder Zylinderwellen sind also keine solchen Wellen, ebene Wellen schon. Ausserdem werden räumlich begrenzte Wellenpakete ausgeschlossen. |
| − |
| |
| − | Bei einer Welle regt eine Schwingung ihren Nachbarn in Ausbreitungsrichtung zu erzwungenen Schwingungen an. Alle schwingen mit der gleichen Frequenz. Die Schwinger hinken aber in Ausbreitungsrichtung der ursprünglichen Schwingung hinterher, wodurch sich eine Phasenverschiebung ergibt. Im Abstand einer halben Wellenlänge beträgt sie gerade LaTex: \pi,so dass die Schwingungen gegenphasig sind, bei einer ganzen Wellenlänge sind es LaTex: 2 \pi, womit die Schwingungen wieder in Phase sind.
| |
| − | Die Welle breitet sich nach rechts aus. Die Schwingungen B, C,... hinken dem linken Nachbar jeweils um hinterher. (Aus den dynamischen Arbeitsblätternzur Wellenlehre.)
| |
| − | Die Welle breitet sich nach rechts aus. Die Schwingungen B, C,... hinken dem linken Nachbar jeweils um LaTex: \pi/4 hinterher. (Aus den dynamischen Arbeitsblätternzur Wellenlehre.)
| |
| − | Inhaltsverzeichnis
| |
| − |
| |
| − | * 1 Zeigermodell
| |
| − | * 2 Wellengleichung
| |
| − | * 3 Versuch: Drehende Holzspirale
| |
| − | * 4 Versuch: Rotierende Perlen
| |
| − | * 5 Links
| |
| − |
| |
| − | [bearbeiten]
| |
| − | Zeigermodell
| |
| − |
| |
| − | Jede Schwingung wird durch einen rotierenden Zeiger dargestellt. Eine Welle wird durch eine Kette von Schwingungen, also auch durch eine Kette von Zeigern dargestellt. Die Zeiger haben eine Phasenverschiebung zum Nachbarzeiger, weil das "Signal" verzögert weitergegeben wird. Das wird in diesem Applet dargestellt.
| |
| − | [bearbeiten]
| |
| − | Wellengleichung
| |
| − |
| |
| − | Man stellt für alle beteiligten Schwinger eine Ortsfunktion auf. Da die Ortsfunktionen von der Position x abhängen, schreibt man LaTex: y_x(t) oder LaTex: y(x,t). Alle Ortsfunktionen zusammen nennt man Wellengleichung.
| |
| − |
| |
| − | Es ergibt sich die Wellengleichung: LaTex: y(x,t) = \hat y \, \sin(\omega t - \varphi(x)) mit der ortsabhängigen Phasenverschiebung LaTex: \varphi(x) = \frac{2 \pi}{\lambda} x.
| |
| − |
| |
| − | [Der Bruch LaTex: \frac{2 \pi}{\lambda} wird auch als Wellenzahl bezeichnet.]
| |
| − |
| |
| − | Woraus folgt: LaTex: y(x,t) = \hat y \, \sin\left( 2\pi \left( \frac{t}{T} - \frac{x}{\lambda}\right) \right)
| |
| − |
| |
| − | [bearbeiten]
| |
| − | Versuch: Drehende Holzspirale
| |
| − | [[Datei:Wellen_Zeigermodell_Holzspirale.jpg|thumb|Die Holzspirale]]
| |
| − |
| |
| − | Versuch: Rotierende Perlen
| |
| − | [[Datei:Wellen_Zeigermodell_rotierende_Perlen.jpg|thumb|Die rotierenden Perlen.]]
| |
| − |
| |
| − |
| |
| − | Links
| |
| − |
| |
| − | * dynamische Arbeitsblätter zur Erarbeitung der Grundbegriffe der Wellenlehre
| |
| − | * Applet: Phasenzeiger einer Welle (Jörg Bogendörfer Didaktik der Physik Uni Erlangen)
| |
| − |
| |
| − |
| |
| − | Im
| |
| − | Falle einer räumlich unbegrenzten, linearen harmonischen Welle kann man
| |
| − | die Welle relativ einfach beschreiben. In einer solchen Welle sind alle
| |
| − | Schwingungen harmonisch und die Welle breitet sich nur längs einer
| |
| − | Raumrichtung aus. Kugelwellen, Kreiswellen oder Zylinderwellen sind
| |
| − | also keine solchen Wellen, ebene Wellen schon. Ausserdem werden
| |
| − | räumlich begrenzte Wellenpakete ausgeschlossen.
| |
| | | | |
| | Bei einer Welle regt eine Schwingung ihren Nachbarn in | | Bei einer Welle regt eine Schwingung ihren Nachbarn in |
| Zeile 55: |
Zeile 9: |
| | sich eine Phasenverschiebung ergibt. Im Abstand einer halben | | sich eine Phasenverschiebung ergibt. Im Abstand einer halben |
| | Wellenlänge beträgt sie gerade <math>\Pi</math>, so dass die Schwingungen gegenphasig sind, bei einer ganzen Wellenlänge sind es <math>2 \ \Pi</math>, womit die Schwingungen wieder in Phase sind. | | Wellenlänge beträgt sie gerade <math>\Pi</math>, so dass die Schwingungen gegenphasig sind, bei einer ganzen Wellenlänge sind es <math>2 \ \Pi</math>, womit die Schwingungen wieder in Phase sind. |
| | + | <br style="clear: both" /> |
| | | | |
| − | [[Bild:Welle_Phasenverschiebung.png|framed|Die Welle breitet sich nach rechts aus. Die Schwingungen B, C,... hinken dem linken Nachbar jeweils um <math>\Pi / 4</math> hinterher. (Aus den [http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/wellen/welleinhalt.html dynamischen Arbeitsblättern zur Wellenlehre].)]]
| |
| | | | |
| | + | ==Zeigermodell== |
| | + | [[Datei:Wellen_Zeigermodell_Holzspirale.jpg|thumb|80px|Die Holzspirale]] |
| | | | |
| | + | Eine Schwingung wird durch einen rotierenden Zeiger dargestellt. Eine Welle wird durch eine Kette von Schwingungen, also auch durch eine Kette von Zeigern dargestellt. Die Zeiger haben eine Phasenverschiebung zum Nachbarzeiger, weil das "Signal" verzögert weitergegeben wird. |
| | | | |
| − | </td></tr></tbody></table><script type="text/javascript"> if (window.showTocToggle) { var tocShowText = "Anzeigen"; var tocHideText = "Verbergen"; showTocToggle(); } </script>
| + | Sehr anschaulich gibt diese Idee eine Holzspirale wieder. Sobald sie sich dreht sieht man eine Welle nach oben oder unten laufen, je nach Drehrichtung. Die einzelnen Holzstäbe sind dabei die Zeiger, die durch ihre Drehung von der Seite betrachtet die Schwingung an einem Ort beschreiben. Jedes Holzstäbchen wird zum Nachbarstäbchen ein bischen gedreht. (Genau genommen sieht man zwei Wellen, weil die Stäbchen zu lang sind.) |
| − | <div class="editsection" style="float: right; margin-left: 5px;">[<a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&action=edit&section=1" title="Abschnitt bearbeiten: Zeigermodell">bearbeiten</a>]</div><a name="Zeigermodell"></a><h2>Zeigermodell</h2>
| + | |
| − | <p>Jede Schwingung wird durch einen rotierenden Zeiger dargestellt.
| + | |
| − | Eine Welle wird durch eine Kette von Schwingungen, also auch durch eine
| + | |
| − | Kette von Zeigern dargestellt. Die Zeiger haben eine Phasenverschiebung
| + | |
| − | zum Nachbarzeiger, weil das "Signal" verzögert weitergegeben wird. Das | + | |
| − | wird in diesem <a href="http://www.bogisoft.de/applets/welle1.htm" class="external text" title="http://www.bogisoft.de/applets/welle1.htm" rel="nofollow">Applet</a> dargestellt.
| + | |
| − | </p>
| + | |
| − | <div class="editsection" style="float: right; margin-left: 5px;">[<a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&action=edit&section=2" title="Abschnitt bearbeiten: Wellengleichung">bearbeiten</a>]</div><a name="Wellengleichung"></a><h2>Wellengleichung</h2>
| + | |
| | | | |
| − | <p>Man stellt für alle beteiligten Schwinger eine Ortsfunktion auf. Da
| + | [[Datei:Wellen_Zeigermodell_rotierende_Perlen.jpg|thumb|Die rotierenden Perlen.]] |
| − | die Ortsfunktionen von der Position x abhängen, schreibt man <img class="tex" src="Zeigermodell%20und%20Wellengleichung-Dateien/mimetex_007.gif" alt="LaTex: y_x(t)"> oder <img class="tex" src="Zeigermodell%20und%20Wellengleichung-Dateien/mimetex.gif" alt="LaTex: y(x,t)">. Alle Ortsfunktionen zusammen nennt man Wellengleichung.
| + | Ähnlich anschaulich sind die auf einem Modell sich drehenden Perlen, die auch schrittweise um einen festen Winkel phasenverschoben sind. |
| − | </p><p>Es ergibt sich die Wellengleichung: <img class="tex" src="Zeigermodell%20und%20Wellengleichung-Dateien/mimetex_004.gif" alt="LaTex: y(x,t) = \hat y \, \sin(\omega t - \varphi(x))"> mit der ortsabhängigen Phasenverschiebung <img class="tex" src="Zeigermodell%20und%20Wellengleichung-Dateien/mimetex_006.gif" alt="LaTex: \varphi(x) = \frac{2 \pi}{\lambda} x">.
| + | |
| − | </p><p>[Der Bruch <img class="tex" src="Zeigermodell%20und%20Wellengleichung-Dateien/mimetex_005.gif" alt="LaTex: \frac{2 \pi}{\lambda}"> wird auch als Wellenzahl bezeichnet.]
| + | |
| − | </p>
| + | |
| − | <pre>Woraus folgt: <img class="tex" src="Zeigermodell%20und%20Wellengleichung-Dateien/mimetex_009.gif" alt="LaTex: y(x,t) = \hat y \, \sin\left( 2\pi \left( \frac{t}{T} - \frac{x}{\lambda}\right) \right)">
| + | |
| − | </pre>
| + | |
| − | <div class="editsection" style="float: right; margin-left: 5px;">[<a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&action=edit&section=3" title="Abschnitt bearbeiten: Versuch: Drehende Holzspirale">bearbeiten</a>]</div><a name="Versuch:_Drehende_Holzspirale"></a><h2>Versuch: Drehende Holzspirale</h2>
| + | |
| − | | + | |
| − | <div class="thumb tnone"><div style="width: 182px;"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Bild:Wellen_Zeigermodell_Holzspirale.jpg" class="internal" title="Die Holzspirale"><img src="Zeigermodell%20und%20Wellengleichung-Dateien/180px-Wellen_Zeigermodell_Holzspirale.htm" alt="Die Holzspirale" longdesc="/wiki/index.php?title=Bild:Wellen_Zeigermodell_Holzspirale.jpg" width="180" height="460"></a> <div class="thumbcaption"><div class="magnify" style="float: right;"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Bild:Wellen_Zeigermodell_Holzspirale.jpg" class="internal" title="vergrößern"><img src="Zeigermodell%20und%20Wellengleichung-Dateien/magnify-clip.htm" alt="vergrößern" width="15" height="11"></a></div>Die Holzspirale</div></div></div>
| + | |
| − | <div class="editsection" style="float: right; margin-left: 5px;">[<a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&action=edit&section=4" title="Abschnitt bearbeiten: Versuch: Rotierende Perlen">bearbeiten</a>]</div><a name="Versuch:_Rotierende_Perlen"></a><h2>Versuch: Rotierende Perlen</h2>
| + | |
| − | <div class="thumb tnone"><div style="width: 182px;"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Bild:Wellen_Zeigermodell_rotierende_Perlen.jpg" class="internal" title="Die rotierenden Perlen."><img src="Zeigermodell%20und%20Wellengleichung-Dateien/180px-Wellen_Zeigermodell_rotierende_Perlen.htm" alt="Die rotierenden Perlen." longdesc="/wiki/index.php?title=Bild:Wellen_Zeigermodell_rotierende_Perlen.jpg" width="180" height="74"></a> <div class="thumbcaption"><div class="magnify" style="float: right;"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Bild:Wellen_Zeigermodell_rotierende_Perlen.jpg" class="internal" title="vergrößern"><img src="Zeigermodell%20und%20Wellengleichung-Dateien/magnify-clip.htm" alt="vergrößern" width="15" height="11"></a></div>Die rotierenden Perlen.</div></div></div>
| + | |
| − | <p><br>
| + | |
| − | </p>
| + | |
| − | <div class="editsection" style="float: right; margin-left: 5px;">[<a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&action=edit&section=5" title="Abschnitt bearbeiten: Links">bearbeiten</a>]</div><a name="Links"></a><h2>Links</h2>
| + | |
| | | | |
| − | <ul><li><a href="http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/wellen/welleinhalt.html#inhalt" class="external text" title="http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/wellen/welleinhalt.html#inhalt" rel="nofollow">dynamische Arbeitsblätter zur Erarbeitung der Grundbegriffe der Wellenlehre</a>
| + | [[Datei:Welle_Zeigermodell_Applet.png|thumb|Eine Welle mit einer Kette von Zeigern. (Aus dem [http://www.bogisoft.de/applets/welle1.htm Applet] von Jörg Bogendörfer)]] |
| − | </li><li><a href="http://www.bogisoft.de/applets/welle1.htm" class="external text" title="http://www.bogisoft.de/applets/welle1.htm" rel="nofollow">Applet: Phasenzeiger einer Welle (Jörg Bogendörfer Didaktik der Physik Uni Erlangen)</a>
| + | In diesem [http://www.bogisoft.de/applets/welle1.htm Applet] ist die Zeigerdarstellung animiert. Leider drehen sich die Zeiger dabei nicht quer zur Ausbreitungsrichtung, sondern parallel dazu. Anders ist es zweidimensional nicht möglich, aber die Darstellung kann auch verwirren. |
| − | </li></ul>
| + | |
| | | | |
| − | <!-- Saved in parser cache with key dbaa020683:pcache:idhash:1575-0!1!0!0!!de!2 and timestamp 20100314112424 -->
| + | ==Wellengleichung== |
| − | <div class="printfooter">
| + | |
| − | Von "<a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung">http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung</a>"</div>
| + | |
| − | <!-- end content -->
| + | |
| − | <div class="visualClear"></div>
| + | |
| − | </div>
| + | |
| | | | |
| − | </div>
| + | Man stellt für alle beteiligten Schwinger eine Ortsfunktion auf. Da die Ortsfunktionen von der Position x abhängen, schreibt man <math>y_x(t)</math> oder <math>y(x,t)</math>. Alle Ortsfunktionen zusammen nennt man Wellengleichung. |
| − | </div>
| + | |
| − | <div id="column-one">
| + | |
| − | <div id="p-cactions" class="portlet">
| + | |
| − | <h5>Views</h5>
| + | |
| − | <ul>
| + | |
| − | <li id="ca-nstab-main" class="selected"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung">Artikel</a></li>
| + | |
| − | <li id="ca-talk" class="new"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Diskussion:Zeigermodell_und_Wellengleichung&action=edit">Diskussion</a></li>
| + | |
| | | | |
| − | <li id="ca-edit"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&action=edit">bearbeiten</a></li>
| + | Jede der einzelnen harmonischen Schwingungen hat die gleiche Frequenz. Sie unterscheiden sich nur durch eine ortsabhängige Phasenverschiebung voneinander: |
| − | <li id="ca-history"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&action=history">Versionen</a></li>
| + | |
| − | </ul>
| + | |
| − | </div>
| + | |
| − | <div class="portlet" id="p-personal">
| + | |
| − | <h5>Persönliche Werkzeuge</h5>
| + | |
| − | <div class="pBody">
| + | |
| | | | |
| − | <ul>
| + | <math>y(x,t) = \hat y \, \sin(\omega t - \varphi(x))</math> |
| − | <li id="pt-login"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Spezial:Userlogin&returnto=Zeigermodell_und_Wellengleichung">Anmelden</a></li>
| + | |
| − | </ul>
| + | |
| − | </div>
| + | |
| − | </div>
| + | |
| − | <div class="portlet" id="p-logo">
| + | |
| − | <a style="background-image: url(/wiki/logo_larissa.jpg);" href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Hauptseite" title="Hauptseite"></a>
| + | |
| − | </div>
| + | |
| | | | |
| − | <script type="text/javascript"> if (window.isMSIE55) fixalpha(); </script>
| + | Eine Schwingung, die eine halbe Wellenlänge vom "Start" entfernt ist, hinkt gerade um <math>\Pi</math> hinterher. Erst eine Schwingung, die eine ganze Wellenlänge vom "Start" entfernt ist, hinkt um <math>2 \ \Pi</math> hinterher und ist damit wieder in Phase. Die ortsabhängige Phasenverschiebung beträgt also |
| − | <div class="portlet" id="p-Navigation">
| + | |
| − | <h5>Navigation</h5>
| + | |
| − | <div class="pBody">
| + | |
| − | <ul>
| + | |
| − | <li id="n-Inhalt-Oberstufe"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Inhalt_Oberstufe">Inhalt Oberstufe</a></li>
| + | |
| − | <li id="n-Inhalt-Klasse-11"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Inhalt_Klasse_11">Inhalt Klasse 11</a></li>
| + | |
| | | | |
| − | <li id="n-Inhalt-Mittelstufe"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Physik_Sekundarstufe_I">Inhalt Mittelstufe</a></li>
| + | <math>\varphi(x) = \frac{2 \pi}{\lambda} x</math>. |
| − | <li id="n-Formelsammlung"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Formelsammlung">Formelsammlung</a></li>
| + | |
| − | <li id="n-Literatur/Links"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Literatur/Links">Literatur/Links</a></li>
| + | |
| − | <li id="n-Rätsel-des-Alltags"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=R%C3%A4tsel_des_Alltags">Rätsel des Alltags</a></li>
| + | |
| − | <li id="n-Spielwiese"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Spielwiese">Spielwiese</a></li>
| + | |
| − | <li id="n-randompage"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Spezial:Random">Zufälliger Artikel</a></li>
| + | |
| | | | |
| − | </ul>
| + | [Der Bruch <math>\frac{2 \pi}{\lambda}</math> wird auch als Wellenzahl bezeichnet.] |
| − | </div>
| + | |
| − | </div>
| + | |
| − | <div class="portlet" id="p-Nützliches">
| + | |
| − | <h5>Nützliches</h5>
| + | |
| − | <div class="pBody">
| + | |
| − | <ul>
| + | |
| − | <li id="n-Hilfe"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=PhysikWiki:Hilfe">Hilfe</a></li>
| + | |
| | | | |
| − | <li id="n-Formatvorlagen"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Formatvorlagen">Formatvorlagen</a></li>
| + | Mit <math>\omega = 2 \ \Pi \ f = \frac{2 \ \Pi}{T}</math>folgt: |
| − | <li id="n-Bilderliste"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Spezial:Imagelist">Bilderliste</a></li>
| + | |
| − | </ul>
| + | |
| − | </div>
| + | |
| − | </div>
| + | |
| − | <div id="p-search" class="portlet">
| + | |
| − | <h5><label for="searchInput">Suche</label></h5>
| + | |
| | | | |
| − | <div id="searchBody" class="pBody">
| + | <math>y(x,t) = \hat y \, \sin\left( 2\pi \left( \frac{t}{T} - \frac{x}{\lambda}\right) \right)</math> Wellengleichung einer linearen harmonischen Welle. |
| − | <form action="/wiki/index.php?title=Spezial:Search" id="searchform"><div>
| + | |
| − | <input id="searchInput" name="search" accesskey="f" type="text">
| + | |
| − | <input name="go" class="searchButton" id="searchGoButton" value="Artikel" type="submit">
| + | |
| − | <input name="fulltext" class="searchButton" value="Suche" type="submit">
| + | |
| − | </div></form>
| + | |
| − | </div>
| + | |
| − | </div>
| + | |
| − | <div class="portlet" id="p-tb">
| + | |
| | | | |
| − | <h5>Werkzeuge</h5>
| |
| − | <div class="pBody">
| |
| − | <ul>
| |
| − | <li id="t-whatlinkshere"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Spezial:Whatlinkshere/Zeigermodell_und_Wellengleichung">Was zeigt hierhin</a></li>
| |
| − | <li id="t-recentchangeslinked"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Spezial:Recentchangeslinked/Zeigermodell_und_Wellengleichung">Verlinkte Seiten</a></li>
| |
| − | <li id="t-upload"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Spezial:Upload">Hochladen</a></li>
| |
| − | <li id="t-specialpages"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Spezial:Specialpages">Spezialseiten</a></li>
| |
| | | | |
| − | <li id="t-print"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&redirect=no&printable=yes&printable=yes">Druckversion</a></li> <li id="t-permalink"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=Zeigermodell_und_Wellengleichung&oldid=3882">Permanentlink</a></li> </ul>
| |
| − | </div>
| |
| − | </div>
| |
| − | </div><!-- end of the left (by default at least) column -->
| |
| − | <div class="visualClear"></div>
| |
| − | <div id="footer">
| |
| − | <div id="f-poweredbyico"><a href="http://www.mediawiki.org/"><img src="Zeigermodell%20und%20Wellengleichung-Dateien/poweredby_mediawiki_88x31.htm" alt="MediaWiki"></a></div>
| |
| | | | |
| − | <div id="f-copyrightico"><a href="http://www.gnu.org/copyleft/fdl.html"><img src="Zeigermodell%20und%20Wellengleichung-Dateien/gnu-fdl.htm" alt="GNU Free Documentation License 1.2"></a></div>
| + | ==Links== |
| − | <ul id="f-list">
| + | |
| − | <li id="lastmod"> Diese Seite wurde zuletzt geändert um 14:43, 19. Dez 2007.</li>
| + | |
| − | <li id="viewcount">Diese Seite wurde bisher 776 mal abgerufen.</li>
| + | |
| − | <li id="copyright">Inhalt ist verfügbar unter der <a href="http://www.gnu.org/copyleft/fdl.html" class="external " title="http://www.gnu.org/copyleft/fdl.html" rel="nofollow">GNU Free Documentation License 1.2</a>.</li>
| + | |
| − | <li id="privacy"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=PhysikWiki:Datenschutz" title="PhysikWiki:Datenschutz">Datenschutz</a></li>
| + | |
| | | | |
| − | <li id="about"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=PhysikWiki:%C3%9Cber_PhysikWiki" title="PhysikWiki:Über PhysikWiki">Über PhysikWiki</a></li>
| + | * [http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/wellen/welleinhalt.html#inhalt dynamische Arbeitsblätter] zur Erarbeitung der Grundbegriffe der Wellenlehre (C. Wolfseher) |
| − | <li id="disclaimer"><a href="http://www.moodle.friedrich.fr.schule-bw.de/wiki/index.php?title=PhysikWiki:Lizenzbestimmungen" title="PhysikWiki:Lizenzbestimmungen">Lizenzbestimmungen</a></li>
| + | * [http://www.bogisoft.de/applets/welle1.htm Applet: Phasenzeiger einer Welle] (Jörg Bogendörfer Didaktik der Physik Uni Erlangen) |
| − | </ul>
| + | |
| − | </div>
| + | |
| − | <script type="text/javascript"> if (window.runOnloadHook) runOnloadHook();</script>
| + | |
| − | </div>
| + | |
| − | <!-- Served by pubwww4.belwue.de in 0.70 secs. -->
| + | |
| − | </div></body></html>
| + | |
Im Falle einer räumlich unbegrenzten, linearen harmonischen Welle kann man die Welle relativ einfach beschreiben. In einer solchen Welle sind alle Schwingungen harmonisch und die Welle breitet sich nur längs einer Raumrichtung aus. Kugelwellen, Kreiswellen oder Zylinderwellen sind also keine solchen Wellen, ebene Wellen schon. Ausserdem werden räumlich begrenzte Wellenpakete ausgeschlossen.
Bei einer Welle regt eine Schwingung ihren Nachbarn in
Ausbreitungsrichtung zu erzwungenen Schwingungen an. Alle schwingen mit
der gleichen Frequenz. Die Schwinger hinken aber in
Ausbreitungsrichtung der ursprünglichen Schwingung hinterher, wodurch
sich eine Phasenverschiebung ergibt. Im Abstand einer halben
Wellenlänge beträgt sie gerade [math]\Pi[/math], so dass die Schwingungen gegenphasig sind, bei einer ganzen Wellenlänge sind es [math]2 \ \Pi[/math], womit die Schwingungen wieder in Phase sind.
Eine Schwingung wird durch einen rotierenden Zeiger dargestellt. Eine Welle wird durch eine Kette von Schwingungen, also auch durch eine Kette von Zeigern dargestellt. Die Zeiger haben eine Phasenverschiebung zum Nachbarzeiger, weil das "Signal" verzögert weitergegeben wird.
Sehr anschaulich gibt diese Idee eine Holzspirale wieder. Sobald sie sich dreht sieht man eine Welle nach oben oder unten laufen, je nach Drehrichtung. Die einzelnen Holzstäbe sind dabei die Zeiger, die durch ihre Drehung von der Seite betrachtet die Schwingung an einem Ort beschreiben. Jedes Holzstäbchen wird zum Nachbarstäbchen ein bischen gedreht. (Genau genommen sieht man zwei Wellen, weil die Stäbchen zu lang sind.)
Ähnlich anschaulich sind die auf einem Modell sich drehenden Perlen, die auch schrittweise um einen festen Winkel phasenverschoben sind.
Man stellt für alle beteiligten Schwinger eine Ortsfunktion auf. Da die Ortsfunktionen von der Position x abhängen, schreibt man [math]y_x(t)[/math] oder [math]y(x,t)[/math]. Alle Ortsfunktionen zusammen nennt man Wellengleichung.
Jede der einzelnen harmonischen Schwingungen hat die gleiche Frequenz. Sie unterscheiden sich nur durch eine ortsabhängige Phasenverschiebung voneinander:
Eine Schwingung, die eine halbe Wellenlänge vom "Start" entfernt ist, hinkt gerade um [math]\Pi[/math] hinterher. Erst eine Schwingung, die eine ganze Wellenlänge vom "Start" entfernt ist, hinkt um [math]2 \ \Pi[/math] hinterher und ist damit wieder in Phase. Die ortsabhängige Phasenverschiebung beträgt also