Aufgaben zur Impulserhaltung (Lösungen): Unterschied zwischen den Versionen
(→Ein Segelboot) |
(→Biliard II) |
||
| Zeile 60: | Zeile 60: | ||
Ausserdem überträgt das Boot durch Reibung Impuls an das Wasser, wodurch es gebremst wird. | Ausserdem überträgt das Boot durch Reibung Impuls an das Wasser, wodurch es gebremst wird. | ||
| − | === | + | ===Billard II=== |
| − | + | [[Datei:Aufgaben_Impuls_Billiard_II_Lösung.jpg|thumb|200px]] | |
| − | [[Datei: | + | *Die Summe der Impulse nach dem Stoß muss gleich dem Impuls vor dem Stoß sein. |
| − | * | + | :Aus der Richtung der Impulsdifferenz kann man auch auf die Richtung der Kraftwirkung schließen: Die Kraft hat auf die weiße Kugel nach links oben gewirkt und auf die schwarze Acht nach rechts unten. |
Version vom 12. Mai 2011, 11:24 Uhr
Inhaltsverzeichnis
Ein Ruderboot
Beim Losfahren drücken die Leute das Wasser nach hinten und sich nach vorne. Das Wasser erhält also Impuls nach hinten und das Boot mit den Leuten den gleichen Impuls nach vorne.
Das Boot schiebt das Wasser am Bug, aber auch durch die Reibung an der Bordwand, nach vorne weg und wird dadurch gebremst. Genauer bekommt das Wasser Impuls nach vorne und genau dieser Impuls fehlt dem Boot.
Elfmeter
Bei einem Elfmeter hält der Torwart den Ball während er springt, also keinen Kontakt zum Boden hat.
- Der Impuls des Balles verteilt sich auf Torwart und Ball. Dadurch erhält auch der Torwart Impuls in Richtung der Torlinie.
- Zur Berechnung der Impulsmenge des Balles braucht man seine (träge) Masse und seine Geschwindigkeit. Der Ball hat eine Masse von ca. 500 g und eine Geschwindigkeit von 100 km/h.
Daraus ergibt sich:
- [math]p = m \, v = 0,5 kg \cdot 27,8 \frac{m}{sec} = 13,9 Hy[/math]
- Der Torwart hat eine Masse von ca. 75 kg. Damit ergibt sich für die Geschwindigkeit von Torwart mit Ball:
- [math]13,9 Hy = 75,5 kg \cdot v[/math]
- [math]v = 13,9 Hy : 75,5 kg = 0,18 \frac{m}{sec} \approx 0,7 \frac{km}{h}[/math]
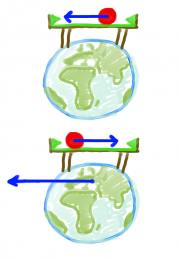
Billiard I
Der Stoßpartner der Kugel ist der Billiardtisch und weil dieser fest mit dem Boden verbunden ist, die gesamte Erdkugel!
Demnach erhält die Erde einen Impuls von [math]2\vec p[/math] nach links.
Diesen Effekt kann man aber nicht sehen, weil die Massen von Billiardkugel und Erdkugel so unterschiedlich sind. Deswegen bewegt sich die Erde nur mit einer winzigen Geschwindigkeit nach links.
Die Billardkugel hat eine Masse von 170 g, die Erde dagegen von [math]5,9736 \cdot 10^{24}[/math] kg. Nimmt man an, dass die Billardkugel sich mit 10 m/sec bewegt, so folgt dementsprechend für die Geschwindigkeit der Erde mit Hilfe einer Impulsbilanz:
- [math]m\, v + M\, V = m\, v' + M \, V'[/math]
- [math]0,170 kg \cdot (-10 m/sec) = 0,170 kg \cdot 10 m/sec + 6 \cdot 10^{24} kg \cdot V' [/math]
- [math]0,170 kg \cdot (-20 m/sec) = 6 \cdot 10^{24} kg \cdot V' [/math]:[math]V' = [/math]
- [math]V' = -10 m/sec \cdot \frac{0,170 kg}{6 \cdot 10^{24} kg} = -10 m/sec \cdot 2,8 \cdot 10^{-26}[/math]
Das sind nur [math]2,8\cdot 10^{-25}m/sec[/math], das entspricht dem Durchmesser eines Atoms in 100 Milliarden Jahren! Nicht besonders schnell also :)
Ein Segelboot
Ein Segelboot hat den Spinnaker gesetzt. Dadurch wird der Rückenwind gebremst.
- Die Luft verliert Impuls nach rechts, den das Boot erhält.
- Luftvolumen: Innerhalb von 10 Sekunden legt die Luft relativ zum Boot eine Strecke von ca. 50m zurück. Damit beträgt das Luftvolumen: [math]V=50 m \cdot 50 m^2 = 2500 m^3[/math]
- Luftmasse: Ein Kubikmeter Luft enthält 1000 Liter und wiegt daher ca. 1 kg. Die Luftmasse beträgt also ca. 2500kg.
- Luftimpuls: [math]p = m \, v = 2500 kg \cdot 5 m/sec = 12500 Hy[/math]
- Änderung des Luftimpulses: Die Luft wird von 5 m/sec nur auf 1 m/sec abgebremst, der Impulsverkust der Luft beträgt daher: [math]\triangle p = 2500 kg \cdot 4 m/sec = 10000 Hy[/math]
- Bootimpuls: Das Boot erhält 10000 Hy.
- Bootgeschwindigkeit: [math]v = \frac{10000 Hy}{2000 kg} = 5 \frac{m}{sec}[/math]
Das Boot ist also nach dieser Abschätzung genausoschnell wie der Wind!? Weil das Spinnaker dann aber die Luft nicht mehr bremsen kann bewirkt es nichts mehr.
- Das Boot wird aber nicht so schnell, denn während der Beschleunigungsphase wird die Luft relativ zum Boot langsamer, also nimmt auch der Impulsübertrag ab, weil das Segel die Luft nicht mehr so stark abbremst.
Ausserdem überträgt das Boot durch Reibung Impuls an das Wasser, wodurch es gebremst wird.
Billard II
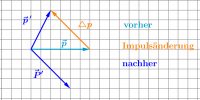
- Die Summe der Impulse nach dem Stoß muss gleich dem Impuls vor dem Stoß sein.
- Aus der Richtung der Impulsdifferenz kann man auch auf die Richtung der Kraftwirkung schließen: Die Kraft hat auf die weiße Kugel nach links oben gewirkt und auf die schwarze Acht nach rechts unten.