Aufgaben zu Energiebilanzen: Unterschied zwischen den Versionen
K (→Beim Klettern) |
(→Beim Radfahren: Unterführung oder Brücke?) |
||
| Zeile 15: | Zeile 15: | ||
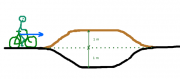
===Beim Radfahren: Unterführung oder Brücke?=== | ===Beim Radfahren: Unterführung oder Brücke?=== | ||
| + | [[Datei:Aufgabe_Energieerhaltung_Unterführung_Brücke.png|thumb]] | ||
An der Dreisam kann sich Elisabeth an einigen Brücken entscheiden, ob sie unter der Brücke hindurchfähren will oder oben entlang. | An der Dreisam kann sich Elisabeth an einigen Brücken entscheiden, ob sie unter der Brücke hindurchfähren will oder oben entlang. | ||
| Zeile 28: | Zeile 29: | ||
*In einer zweiten Betrachtung tritt sie gerade soviel in die Pedale, dass die Reibung ausgeglichen wird. Die Reibung, also auch der Energie"verlust" ist bei größeren Geschwindigkeiten auch größer. | *In einer zweiten Betrachtung tritt sie gerade soviel in die Pedale, dass die Reibung ausgeglichen wird. Die Reibung, also auch der Energie"verlust" ist bei größeren Geschwindigkeiten auch größer. | ||
:Welcher Weg ist für Elisabeth energetisch günstiger? | :Welcher Weg ist für Elisabeth energetisch günstiger? | ||
| − | |||
| − | |||
===Eine Federschwingung=== | ===Eine Federschwingung=== | ||
Version vom 23. Mai 2011, 09:52 Uhr
Inhaltsverzeichnis
Ein LKW im Stadtverkehr
Ein voll beladenener 40-Tonner hält bei seiner Fahrt durch die Stadt an fünf roten Ampeln und beschleunigt jedesmal wieder auf 50 km/h.
- Wieviel Energie benötigt er nur für die Beschleunigungen?
- Wieviel Diesel benötigt er wohl dazu?
- Diesel hat einen Energiegehalt von ca. 37 MegaJoule. (Siehe Wikipedia: Heizwert) Der Wirkungsgrad des Dieselmotors liegt bei ca. 1/3. Das heißt 2/3 der Energie werden zur Erärmung des Motors und der Abgase verwendet. (Siehe: Wikibooks: Motoren aus technischer Sicht; oder Energie-Lexikon.info)
- Auf dem Rückweg fährt er wieder an den fünf Ampeln vorbei, ist aber diesmal leer mit einer Masse von nur 20 Tonnen. Wieviel Diesel benötigt er nun?
Beim Klettern
Elisabeth fällt beim Vorsteigen ins Seil. Der nächste Haken ist drei Meter unter ihr.
- Wieviel Energie muss das Seil durch Dehnung und Reibung aufnehmen, wenn sie eine Masse von 60 kg hat? (und bei ihrer Tochter Erika mit nur 30 kg?)
- Wie schnell ist Elisabeth, wenn sie ins Seil fällt? (und Erika?)
Beim Radfahren: Unterführung oder Brücke?
An der Dreisam kann sich Elisabeth an einigen Brücken entscheiden, ob sie unter der Brücke hindurchfähren will oder oben entlang.
Welche Vor- oder Nachteile haben die beiden Möglichkeiten eigentlich? Interessant wäre auf welchem Weg sie schneller ist und auf welchem Weg sie weniger Energie benötigt.
Als Rechenbeispiel zur Abschätzung kann man annehmen, dass der Weg oben entlang einen Meter höher liegt und der Weg unten einen Meter tiefer. Elisabeth wiegt mit ihrem Rad zusammen 90 kg fährt mit 18 km/h auf die Brücke zu.
- Zunächst nehmen wir der Einfachheit halber an, dass die Reibung an Luft und Boden keine große Rolle spielt und Elisabeth unter oder auf der Brücke nur noch rollt ohne zu Treten.
- Wie ist dann der Geschwindigkeitsverlauf, wenn sie oben oder unten fährt? Auf welchem Weg ist sie daher schneller?
- Berechne Elisabeths Geschwindigkeit unter oder auf der Brücke.
- In einer zweiten Betrachtung tritt sie gerade soviel in die Pedale, dass die Reibung ausgeglichen wird. Die Reibung, also auch der Energie"verlust" ist bei größeren Geschwindigkeiten auch größer.
- Welcher Weg ist für Elisabeth energetisch günstiger?
Eine Federschwingung
Ein Wagen ist durch einer Feder am Tisch befestigt. Der Wagen wird ein Stück nach rechts geschoben und losgelassen.
- Beschreibe die Bewegung, die der Wagen dann macht.
- Beschreibe, wie sich der Ort der Energie (die Energieform) im Laufe der Zeit ändert.
- Zur genaueren Beschreibung hat man die Federkonstante zu 0,5 N/cm und die Masse des Wagens zu 100 Gramm bestimmt. Der Wagen wird aus der Position mit entspannter Feder um 2 cm nach rechts ausgelenkt und losgelassen.
- Wie schnell wird der Wagen maximal?
- Wie schnell wird er, wenn man bei gleicher Auslenkung die Masse des Wagens durch ein 300g-Gewicht vervierfacht?
- Wie schnell wird er, wenn man den 100 Gramm trägen Wagen 4 Zentimeter auslenkt?