Das Konzept der Energie: Unterschied zwischen den Versionen
(→Links) |
K (→Aufbau:) |
||
| Zeile 134: | Zeile 134: | ||
*Erstellen Sie zunächst ein Diagramm des zeitlichen Temperaturverlaufs T(t). (T ist die absolute Temperatur in Kelvin.) Wie interpretieren Sie den Verlauf? | *Erstellen Sie zunächst ein Diagramm des zeitlichen Temperaturverlaufs T(t). (T ist die absolute Temperatur in Kelvin.) Wie interpretieren Sie den Verlauf? | ||
| − | *Bestimmen Sie die die Wärmeenergiekapazität von Wasser | + | *Bestimmen Sie die die Wärmeenergiekapazität und die Verdampfungsenergie von Wasser. (In der Chemie spricht man von Verdampfungsenthalpie.) |
*Können Sie auch angeben, wieviel Entropie man benötigt, um ein Kilogramm Wasser zu verdampfen? | *Können Sie auch angeben, wieviel Entropie man benötigt, um ein Kilogramm Wasser zu verdampfen? | ||
*Wieviel Entropie benötigt man bei der Erwärmung des Wassers? | *Wieviel Entropie benötigt man bei der Erwärmung des Wassers? | ||
| − | |||
==Links== | ==Links== | ||
*[http://schulen.eduhi.at/riedgym/physik/10/waerme/entropie/start_entropie.htm Entropieerklärung (Gymnasium Ried)] | *[http://schulen.eduhi.at/riedgym/physik/10/waerme/entropie/start_entropie.htm Entropieerklärung (Gymnasium Ried)] | ||
*[http://elearning.zhaw.ch/moodle/mod/book/print.php?id=48690 E-Learning ZHAW Kurs: Thermodynamik (maur) Buch: Theorie Wärme] | *[http://elearning.zhaw.ch/moodle/mod/book/print.php?id=48690 E-Learning ZHAW Kurs: Thermodynamik (maur) Buch: Theorie Wärme] | ||
Version vom 19. Oktober 2011, 23:02 Uhr
Inhaltsverzeichnis
- 1 Einführung und Beispiele
- 2 Berechnung der Energiemengen bei konstantem Beladungsmaß (Potential)
- 3 Energieübertragung bei Fließgleichgewicht
- 4 Praktikum: Der Energie- und Entropiefluß eines Mini-Kraftwerks
- 5 Praktikum: Bestimmung von Energie- und Entropiekapazität von Wasser und Wasserdampf
- 6 Links
Einführung und Beispiele
Energiemenge eines Wassergefüllten Glases
- Es gibt verschiedene Energieträger (Energieformen):
- warme Gegenstände: Entropie (thermische Energie)
- zusammengedrückte oder auseinandergezogene Gegenstände: ??? (Spannenergie)
- hochgehobene Gegenstände: Schwerefeld (Lageenergie)
- sich bewegende Gegenstände: Impuls (Bewegungsenergie)
- Bei einigen Energieträgern ist die enthaltene Energiemenge vom Bezugssystem abhängig:
- Schwerefeld (Lageenergie)
- Impuls (Bewegungsenergie)
- Energie ist das Geld der Physik. Man bewertet damit Situationen.
- Es ist alles andere als selbstverständlich, daß wirklich sämtliche Situationen vergleichbar und in einer Einheit auch bewertbar sind.
- Energie ist eine Erhaltungsgröße, sie kann weder erzeugt, noch vernichtet werden. (Im Gegensatz zum Geld gibt es auch weder Inflation noch Deflation :)
- In der Regel ist die absolute Energiemenge eines Körpers uninteressant. Man interessiert sich viel mehr für die Energiemengen, die hinaus oder hineingehen.
- Die Veränderungen der Energiemenge kann man durch einen Energiestrom beschreiben, bei dem gleichzeitig auch der Energieträger strömt.
- Um eine gespeicherte Energiemenge zu bestimmen, muss man den heraus- oder hereinfließenden Energiestrom integrieren.
- Es ist (leider!?) auch üblich der gespeicherten Energie einen anderen Namen zu geben als der Energie, welche strömt. Man nennt die gespeicherte Energie eine Zustandsgröße, die strömende eine Prozessgröße.
Zustandsgröße Prozessgröße mechanische Energie mechanische Arbeit thermische Energie Wärme
| Name der Energie | Mengenartige (extensive) Größen (Energieträger) | haben zugehörige Eigenschaften (intensive Größen) (Potential / Beladungsmaß) |
| E: Energiemenge [math][E]=\mathrm{J \quad(Joule)}[/math] | ||
| Wärmeenergie | S: Entropiemenge [math][S] = \mathrm{Ct \quad (Carnot)}[/math] | T: absolute Temperatur [math][T] = \mathrm{K \quad (Kelvin)} =\frac{J}{Ct}[/math] |
| Druckenergie | V: Volumen [math][V] = \mathrm{m^3}[/math] | p: Druck [math][p] = \mathrm{Pa \quad (Pascal) = 10^{-5}bar}=\frac{J}{m^3}[/math] |
| Lageenergie | m: Masse [math][m] = \mathrm{kg}[/math] | gh: Schwerepotential [math][gh] = \mathrm{m^2/{s^2} }=\frac{J}{kg}[/math] |
| Bewegungsenergie | p: Impuls [math][p] = \mathrm{Hy \quad (Huygens)= kg \frac{m}{s}} [/math] | v: Geschwindigkeit [math][v] = \mathrm{m/s} =\frac{J}{Hy}[/math] |
| elektrische Energie | Q: el. Ladung [math][Q] = \mathrm{C \quad (Coulomb)}[/math] | φel: el. Potential [math][\varphi_{el}] = \mathrm{V \quad (Volt)}=\frac{J}{C}[/math] |
| chemische Energie | n: Stoffmenge [math][n] = \mathrm{mol}[/math] | μ: chem. Potential (freie molare Standardenthalpie) [math][\mu] = \mathrm{J/{mol} \quad (Joule/Mol)}[/math] |
Berechnung der Energiemengen bei konstantem Beladungsmaß (Potential)
Schokolade
Bei einer Tafel Schokolade steht auf der Packung: Brennwert pro 100g: 2570 kJ.
Das bedeutet, dass ihr chemisches Potential [math]\varphi_{ch}=25700 \frac{kJ}{kg} \approx 26 \frac{MJ}{kg}[/math]beträgt.
Bei einer Masse von 200g ergibt sich:
[math]E= 0,2 kg \cdot 25700 \frac{kJ}{kg} = 5140 kJ \approx 5 MJ[/math]
Atombombe
Auch bei einer Atombombe ist das Beladungsmaß konstant, es gilt nämlich die berühmte Formel:
[math]E= m \, c^2[/math]
Das heißt, die Masse der Atomkerne ist der Energieträger und wenn diese sich bei der Kettenreaktion verkleinert, so speichern die Kerne weniger Energie.
Der Faktor [math]c^2[/math] gibt an, wie stark die Masse mit Energie beladen ist, nämlich mit [math]299792458^2 \frac{J}{kg} \approx 9 \cdot 10^{16} \frac{J}{kg} = 90000000 \frac{MJ}{kg}[/math]. Das ist eine ganze Menge!
Benzin
Zum Vergleich: Benzin hat ein chemisches Potential von ca. [math]40 \frac{MJ}{kg}[/math].
Energieübertragung bei Fließgleichgewicht
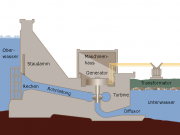
Ein Wasserkraftwerk
Ein Wasserkraftwerk versorgt Haushalte und Industrie mit Strom. Es benutzt die Energie, die im aufgestauten Wasser enthalten ist, um den elektrischen Strom anzutreiben.
Genauer wird die Energie vom Wasser auf die bewegte Turbine und die Generatorwelle umgeladen. Danach wird im Generator die Energie von der Bewegung auf die Elektrizität umgeladen.
Während das Kraftwerk läuft, fließt ein konstanter Energiestrom vom Wasser bis in die elektrische Ladung.
Ebenso sind die Ströme der Energieträger konstant: Der Wasserstrom in die Turbine hinein und heraus ist konstant. Der Impuls der Turbine ist auch konstant, denn es fließt genausoviel Impuls hinein, wie heraus. (Oder, anders ausgedrückt, die anteibende und die bremsende Kraft ist gleichgroß.) Ebenso fließt genausoviel elektrische Ladung in den Generator hinein wie heraus. Daher spricht man bei jeder Umladung von einem Fließgleichgewicht.
Bei jeder Umladung verändert sich das Beladungsmaß des Energieträgers: Zunächst nimmt der Druck des Wassers stark ab, was anzeigt, dass das Wasser seine Energie abgibt. Diese Energie wird genutzt, um Impuls von der Erde auf das Turbinenrad zu übertragen. Die Geschwindigkeit des Impulses nimmt zu. Im Generator passieren zwei Dinge: Einerseits wird die Turbine gebremst, der Impuls kommt wieder auf ein niedriges Geschwindigkeitsniveau, und andererseits wird die elektrische Ladung von einem niedrigen Potential auf ein hohes angehoben. Wird nun vom Strom eine Lampe betrieben, so fällt das elektrische Potential hinter der Lampe wieder ab. Die Ladung hat ihre Energie wieder abgegeben.
(Bemerkung: In der Umgangssprache heißen die großen Energie"lieferanten", welche den Strom aus der Steckdose fließen lassen aus historischen Gründen "Kraftwerke", obwohl sie uns gar keine Kraft im physikalischen Sinne liefern.)
Praktikum: Der Energie- und Entropiefluß eines Mini-Kraftwerks
Praktikum: Bestimmung von Energie- und Entropiekapazität von Wasser und Wasserdampf
Aufbau:
- Materialien:
- 1. Behälter(Plastikeimer ca. 1 Liter, Styroporbecher ca. 1/2 Liter, etc.)
- 2. 1 Tauchsieder (ca.230W/ca.1000W)
- 3. Bestimmte Menge Wasser
- 4. Stoppuhr
- 5. Waage
- 6. Leistungsmesser
- 7. Thermometer
Zu messsen: Das Ziel ist es, herauszufinden wieviel Entropie und Energie sich in Wasser und Wasserdampf befindet.
Dazu erhitzt man eine gewisse Menge Wasser mit einem Tauchsieder und läßt es dann eine Weile kochen. Durch Messung der Leistung des Tauchsieders bestimmt man die zugeführte Energiermenge. Während des Erwärmens wird ständig die Temperatur und die verstrichene Zeit gemessen und danach auch die Menge des verdampften Wassers bestimmt.
- Erstellen Sie zunächst ein Diagramm des zeitlichen Temperaturverlaufs T(t). (T ist die absolute Temperatur in Kelvin.) Wie interpretieren Sie den Verlauf?
- Bestimmen Sie die die Wärmeenergiekapazität und die Verdampfungsenergie von Wasser. (In der Chemie spricht man von Verdampfungsenthalpie.)
- Können Sie auch angeben, wieviel Entropie man benötigt, um ein Kilogramm Wasser zu verdampfen?
- Wieviel Entropie benötigt man bei der Erwärmung des Wassers?