Aufgaben zur Kinematik (Bewegungslehre): Unterschied zwischen den Versionen
Aus Schulphysikwiki
(→Bewegungsdiagramme) |
K (→Bewegungsdiagramme) |
||
| Zeile 26: | Zeile 26: | ||
==Bewegungsdiagramme== | ==Bewegungsdiagramme== | ||
| − | + | ===1) Ein Ortsdiagramm interpretieren=== | |
[[Datei:Kinematik_Aufgabe_Ortsdiagramm_Elisabeth.png|800px]] | [[Datei:Kinematik_Aufgabe_Ortsdiagramm_Elisabeth.png|800px]] | ||
:a) Erzähle eine Gschichte passend zum Ortsdiagramm der Bewegung. | :a) Erzähle eine Gschichte passend zum Ortsdiagramm der Bewegung. | ||
| Zeile 45: | Zeile 45: | ||
:- Die Fläche zwischen der t-Achse und dem Schaubild der Funktion ergibt die Änderung des Ortes. | :- Die Fläche zwischen der t-Achse und dem Schaubild der Funktion ergibt die Änderung des Ortes. | ||
| − | + | ===2) Zeichne qualitativ das Ortsdiagramm zu folgender Geschichte:=== | |
:''Elisabeth muss zur Post. Sie schwingt sich auf ihr Rad und fährt gemütlich mit konstanter Geschwindigkeit. Pfeifend genießt sie das schöne Herbstwetter.'' | :''Elisabeth muss zur Post. Sie schwingt sich auf ihr Rad und fährt gemütlich mit konstanter Geschwindigkeit. Pfeifend genießt sie das schöne Herbstwetter.'' | ||
Version vom 2. Oktober 2014, 15:21 Uhr
Inhaltsverzeichnis
Grundlegendes
- Welche Fragen beantwortet die Kinematik?
- -Wann ist ein beobachter Gegenstand wo? Und wie schnell ist er? Es ist die Lehre von der Bewegung.
- Wozu braucht man ein Koordinatensystem?
- -Um auf einfache Weise genaue Orts- und Zeitbestimmungen zu dokumentieren.
- Was versteht man unter [math]\dot s[/math], der momentanen zeitlichen Änderungsrate des Ortes?
- -[math]\dot s[/math] ist die Geschwindigkeit
- Warum ist die Geschwindigkeit eine vektorielle Größe, die Masse aber nicht?
- -Vektoren werden durch Betrag und Richtung festgelegt. Um eine Geschwindigkeit eindeutig zu bestimmen, benötigt man Betrag und Richtung. Die Masse eines Gegenstandes hat keine Richtung.
- Nenne weitere vektorielle und skalare Größen mit ihren Einheiten.
- -vektoriell: Beschleunigung (m/s^2), Kraft (N), Impuls (kg· m/s oder Hy)
- -skalar: Masse (kg), Zeit (s),Temperatur (K oder °C), Energie (J oder kWh)
- Bei welchen Bewegungen unterscheidet sich der zurückgelegte Weg von der Änderung des Ortes?
- - Läuft eine Person einen Halbkreis auf dem Boden, so ist die gesamte Änderung des Ortes gerade der Durchmesser des Kreises. Der zurückgelegte Weg ist aber der halbe Umfang und somit länger, die Person ist ja auch einen Umweg gelaufen.
- Läuft die Person sogar einmal im Kreis, so gibt es gar keine Ortsänderung aber natürlich einen zurückgelegten Weg.
- Auch wenn eine Person auf einer geraden Linie zunächst nach recht und dann wieder zurück läuft, ist die Änderung des Ortes viel kleiner als der zurückgelegte Weg.
Bewegungsdiagramme
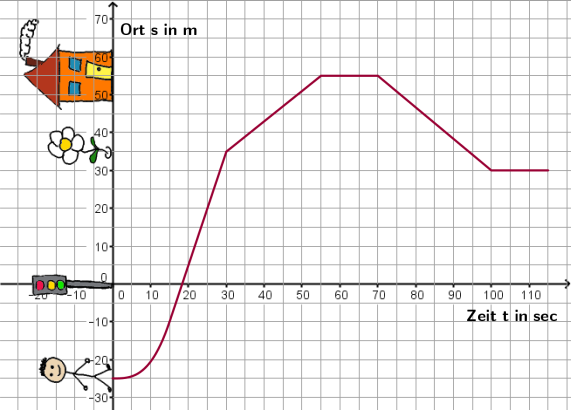
1) Ein Ortsdiagramm interpretieren
- a) Erzähle eine Gschichte passend zum Ortsdiagramm der Bewegung.
- b) Wie schnell ist die Person zwischen
- [math]t = 15 \, \rm sec[/math] und [math]t = 30 \, \rm sec[/math]
- [math]t = 30 \, \rm sec[/math] und [math]t = 55 \, \rm sec[/math]
- [math]t = 30 \, \rm sec[/math] und [math]t = 100 \, \rm sec[/math]?
- c) Wie schnell ist sie zum Zeitpunkt [math]t = 10 \, \rm sec[/math]?
- Skizziere zu den Bewegungen jeweils das Ort-Zeit-Diagramm und das Geschwindigkeit-Zeit-Diagramm.
- gleichförmige Bewegung mit 4 m/s; Beginn der Zeitmessung bei einer Ampel
- gleichförmig beschleunigte Bewegung mit 2 m/s^2; Beginn der Zeitmessung: Stehend an einer Ampel
- Wie kann man die momentante und wie die Durchschnittsgeschwindigkeit an einem s-t-Diagramm ablesen?
- - Momentangeschwindigkeit: Ableitung/Steigung - Durchschnittsgeschwindigkeit: Sekante
- Wie kann man die Änderung des Ortes (meistens der zurückgelegte Weg) an einem v-t-Diagramm ablesen?
- - Die Fläche zwischen der t-Achse und dem Schaubild der Funktion ergibt die Änderung des Ortes.
2) Zeichne qualitativ das Ortsdiagramm zu folgender Geschichte:
- Elisabeth muss zur Post. Sie schwingt sich auf ihr Rad und fährt gemütlich mit konstanter Geschwindigkeit. Pfeifend genießt sie das schöne Herbstwetter.
- Nach einem Blick auf die Uhr stellt sie erschrocken fest, dass die Post gleich schließt. Deshalb fährt sie jetzt so schnell sie kann (gleichförmig) weiter und schafft es zum Glück gerade noch. In der Post sind noch viele andere Leute und so dauert es eine Weile, bis sie ihren Heimweg antreten kann.
- Sie fährt den gesamten Rückweg mit konstanter Geschwindigkeit und hält nur einmal kurz an, um ihrem Liebsten eine Blume zu pflücken. Die Rückfahrt dauert ungefähr genauso lange wie die Hinfahrt.