Aufgaben zur Newtonschen Mechanik (Dynamik): Unterschied zwischen den Versionen
(→Einheitenpuzzle und Sprachwirrwarr) |
(→Die Weltraumwaage SLAMMD) |
||
| Zeile 112: | Zeile 112: | ||
==Praktische Anwendungen== | ==Praktische Anwendungen== | ||
====Die Weltraumwaage SLAMMD==== | ====Die Weltraumwaage SLAMMD==== | ||
| − | Das "Space Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. ([http://www.youtube.com/watch?v=qE4OoE93fX0 Demovideo]) | + | Das "Space Linear Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. ([http://www.youtube.com/watch?v=qE4OoE93fX0 Demovideo]) |
Bei einer Messung wurde die Person durch eine Kraft von 50 Newton in 1,2 Sekunden auf eine Geschwindigkeit von 0,8 Meter pro Sekunde beschleunigt. | Bei einer Messung wurde die Person durch eine Kraft von 50 Newton in 1,2 Sekunden auf eine Geschwindigkeit von 0,8 Meter pro Sekunde beschleunigt. | ||
*Wie groß ist deren (träge) Masse? | *Wie groß ist deren (träge) Masse? | ||
| − | |||
====Der Anschnallgurt==== | ====Der Anschnallgurt==== | ||
Version vom 4. Dezember 2014, 10:51 Uhr
Inhaltsverzeichnis
Grundlagen
2. Newtonsches Gesetz
- Wie lautet das 2. Newtonsche Gesetz?
- Erläutere es auch an einem selbstgewählten Beispiel.
Das Wasserbehältermodell I
- In der Tabelle ist außer der ersten Spalte einiges durcheinandergeraten. Sortiere es wieder richtig.
| Bewegung | Wasserbehälter | ||
|---|---|---|---|
| Impulsmenge | (in Newton) | Grundfläche | (in ml/s) |
| Masse | (in Newton) | Wassermenge | (in ml/s) |
| Geschwindigkeit | (in Huygens) | Abflussrate | (in cm) |
| Kraft | (in m/s) | Zuflussrate | (in cm2 ) |
| Reibungskraft | (in kg) | Wasserhöhe | (in ml) |
Einheitenpuzzle und Sprachwirrwarr
Einige dieser Aussagen sind richtig. Einige nicht. Finde die richtigen!
Tipps:
- Impuls ist eine Menge von Bewegung: "viel Impuls", "wenig Impuls". Ersetze das Wort "Impuls" durch "Wassermenge".
- Kraft ist die Veränderung der Bewegungsmenge mit der Zeit: "große Kraft", "kleine Kraft". Ersetze das Wort "Kraft" durch "Zu-/Abfluss".
|
|
Das Wasserbehältermodell II
Beschreibe jeweils die Situationen oder Abläufe, indem du passende Wasserbehältermodelle findest.
- Paul und Pauline fahren Skatebord
- Paul und Pauline stehen mit ihrem Skateboard auf der Straße. Beide stoßen sich für eine halbe Sekunde mit einer Kraft von 80 Newton vom Boden ab. Paul hat aber doppelt so viel Masse wie Pauline.
- Pauline und Antonia fahren zusammen Fahrrad
- Beide haben in etwa die gleiche Masse und sind auch gleichschnell. Vor der Ampel kommt Pauline innerhalb von drei Sekunden zum Stehen. Antonia dagegen kann mit ihren besseren Bremsen sogar in anderthalb Sekunden anhalten.
- Paul zieht Pauline auf dem Schlitten
- Zunächst geht es mit einer gleichbleibenden Geschwindigkeit über den Schnee. Dann aber kommt eine Straße und Paul zieht so, dass sie trotzdem die Geschwindigkeit beibehalten. Schließlich aber bleibt der Schlitten stecken und trotz Ziehens ist der Schlitten nicht mehr zu bewegen.
- Pauline fährt Rad
- Zuerst steht sie an der Ampel. Dann tritt sie mit einer gleichbleibenden Kraft in die Pedale, bis sie schließlich mit konstanter Geschwindigkeit fährt. Nach einer Weile hört sie auf zu treten und läßt es gemütlich ausrollen.
Jemanden anschieben
Moritz wird von Karla wird auf einem Bürodrehstuhl angeschoben. Seine (träge) Masse beträgt 70kg und die des Stuhls 10kg. Dabei wird er 2 m/sec schnell.
- Wieviel Impuls steckt in Moritz und wieviel im Stuhl?
- Mit welcher mittleren Kraft schiebt Karla, wenn sie eine halbe (ganze) Sekunde lang geschoben hat?
- Welche Strecke legt Moritz dabei zurück?
Losfahren
Marlene beschleunigt auf ihrem Rad aus dem Stand 10 Sekunden lang mit einer mittleren Kraft von 30 Newton. Zusammen mit dem Rad hat sie eine (träge) Masse von 60kg.
- Wie schnell wird sie? (Gib das Ergebnis auch in km/h an.)
- Längs welcher Strecke hat sie beschleunigt?
Roller fahren
Tina steht mit ihrem Roller auf einer ebenen Straße. Zusammen haben sie eine Masse von 50kg. Dann schubst sie sich zweimal von der Straße ab. Beim ersten Mal eine Sekunde lang mit einer Kraft von 100N, beim zweiten Mal eine halbe Sekunde lang mit einer Kraft von 60N. Dazwischen rollt sie für zwei Sekunden.
- Wieviel Impuls hat Tina nach dem ersten und nach dem zweiten Anschubsen und wie schnell ist sie jeweils? (Rechne ohne Reibung, also ohne Impulsverlust.)
- Zeichne das Impuls-Zeit- und Kraft-Zeit-Diagramm für die drei Sekunden dauernde Fahrt. Zeichne das passende Geschwindigkeit-Zeit-Diagramm.
- Wie weit fährt Tina in dieser Zeit?
Die gerade eben noch vernachlässigte Reibungskraft beträgt für Tina und ihren Roller konstant 10 Newton.
- Wie lange nach dem zweimaligen Anschubsen kann Tina noch rollen, bevor sie stehen bleibt?
- Welche Strecke kann legt sie beim Ausrollen zurück?
- Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren?
Widerstände beim Radfahren
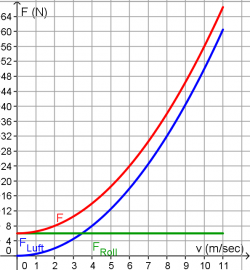
In diesem Widerstandsdiagramm ist die Reibungskraft F über die Geschwindigkeit aufgetragen. Die Reibungskraft setzt sich aus dem geschwindigkeitsunabhängigen Rollwiderstand und der Luftreibung zusammen.
Paula fährt auf ebener Strecke mit einer konstanten Geschwindigkeit von 6 m/s.
- Wie groß ist jetzt die Reibungskraft und wie groß die antreibende Kraft?
Danach tritt Paula so in die Pedale, dass die antreibende Kraft auf 40N ansteigt.
- Wie schnell wird sie jetzt?
Praktische Anwendungen
Die Weltraumwaage SLAMMD
Das "Space Linear Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. (Demovideo)
Bei einer Messung wurde die Person durch eine Kraft von 50 Newton in 1,2 Sekunden auf eine Geschwindigkeit von 0,8 Meter pro Sekunde beschleunigt.
- Wie groß ist deren (träge) Masse?
Der Anschnallgurt
Der Gurt verhindert bei einem Autounfall stärkere Verletzungen.
Wie groß sind wohl die Kräfte auf den Kopf der FahrerIn bei einem Aufprall mit 50 km/h auf ein festes Hindernis mit und ohne Gurt?
Mit Hilfe dieses Videos vom TCS wurde die Zeitdauer des Abremsens des Kopfes mit und ohne Gurt abgeschätzt. In den Zeitlupenaufnahmen wurden ca. 500 Bilder pro Sekunde aufgenommen, also alle 2 msec ein Bild gemacht.
- Abremsen durch Aufprall auf Frontscheibe und Lenkrad: ca. 6 msec
- Abremsen durch den Gurt: ca. 44 msec
Ein menschlicher Kopf hat eine Masse von ca. 3-4kg ([1], [2]).
- Berechne die wirkenden Kräfte beim Abbremsen und vergleiche sie mit der Gewichtskraft des Kopfes.
Weihnachtsbaumtransport
In diesem Video des ADAC wurde der Transport eines Weihnachtsbaumes auf dem Autodach untersucht.
Zitat: "Ein mannshohe Tanne bringt um die 30kg auf die Waage. Bei einem Aufprall mit 50km/h zerren in diesem Fall 750kg am Dachträger."
- Wie ist das zu verstehen, dass die Masse der Tanne auf einmal viel größer ist? Sind da ein paar Äste gewachsen?
- In welcher Zeitspanne wird die Tanne abgebremst? (Berechne dazu zuerst den Impuls der Tanne und wie stark die Spanngurte an der Tanne ziehen.)
Turmspringen
Eine Turmspringerin läßt sich vom 10-Meter-Turm fallen. Sie hat eine Masse von 60 kg.
- Mit welcher Kraft wird sie beschleunigt?
- Wie groß ist ihr Impuls und ihre Geschwindigkeit nach 1, 2, 3 Sekunden? (nach t Sekunden?)
- Vergleiche mit dem Fall ihres um 20kg "schwereren" Vereinskameraden.
- die Impuls- und Geschwindigkeitszunahme,
- den Aufprall auf der Wasseroberfläche.
Mit dem Fahrrad bergab rollen
Anna rollt aus dem Stand den Schauinsland herunter. Sie möchte gerne wissen, wie schnell sie nach einer gewissen Zeit wird und welche maximale Geschwindigkeit sie erreichen kann.
Dazu bestimmt sie das Gefälle der Straße zu 10%, ihre Masse zu 50 kg, die Masse des Rads zu 10 kg und im Internet findet sie noch ein Diagramm, das ihr angibt wie die Widerstandskraft von der Geschwindigkeit abhängt.
- Warum kann man für die Betrachtung der ersten drei Sekunden der Bewegung den Luftwiderstand noch vernachlässigen?
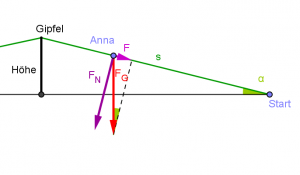
- Um die beschleunigende Kraft zu berechnen, rechnet Anna:
- [math]F_G = 60\,\rm kg \cdot 10\frac{\rm N}{\rm kg}[/math]
- und weiter:
- [math]\tan \alpha = \frac{F}{F_N} \approx \frac{F}{F_G} = \frac{1\,\rm km}{10\,\rm km} = 10\% [/math]
- [math] \Rightarrow \quad F = F_G \cdot 10\%[/math]
- und dann zieht sie von diesem Ergebnis noch 6 Newton ab.
Begründe ihre Rechnung und berechne die beschleunigende Kraft.
- Wie schnell wird Anna innerhalb der ersten drei Sekunden? Zeichne ein Geschwindigkeitsdiagramm (x: Zeit ; y: Geschwindigkeit) der ersten drei Sekunden.
- Nach ca. einer Minute Rollen hat Anna schon ihre maximale Geschwindigkeit erreicht.
- Bestimme mit Hilfe des Widerstands-Diagramms Annas maximale Geschwindigkeit.
- Zeichne das Geschwindigkeitsdiagramm der ersten Minute.
Wasserwerfer
Der Wasserstrahl eines Wasserwerfers hat soviel Impuls, dass er Menschen umwerfen kann. Hält man in einem vereinfachten Experiment ein Brett in den Wasserstrahl eines Gartenschlauchs, so spürt man eine Kraft. Mit dieser Kraft wird das Wasser bis zum Stillstand abgebremst!
Aus einem Schlauch spritzen pro Minute 6 Liter Wasser. Man misst eine Kraft von 0,5 Newton auf das Brett.
- Wie schnell ist das Wasser?
Am Wasserhahn
Bestimme die Austrittsgeschwindigkeit des Wassers am Hahn.
Man hat folgende Hilfsmittel zur Verfügung: eine Waage (mit einer Plastiktüte zum Schutz), ein Messbecher und eine (Stopp-)Uhr.
Beschreibe den Aufbau, die Messergebnisse und die Auswertung.
vektorielle Impulsänderung
Pelton-Turbine
Hält man statt des Bretts eine Schale in den Wasserstrahl, die den Strahl um 180° umlenkt, kann man eine (fast) doppelt so große Kraft messen.
(Dieser Effekt wird bei der sogenannten Pelton-Wasserturbine ausgenutzt. Verschiedene Videos dazu: 1Pelton Turbine/Wheel Working & Design, 2WATER TURBINE PELTON COSTA RICA, 3Pelton-Turbine (Aufbau und Funktionsweise) 3D-Animation)
- Warum ist die Kraft (fast) doppelt so groß?
Impuls- und Kraft-Diagramme
Auf dem Skateboard - Anschubsen
Die folgenden Aufgaben kann man mit dieser Animation der Bewegungsdiagramme lösen!
Pauline und Paul fahren Skateboard. Pauline ist kleiner und bringt deshalb nur 50kg auf die Waage im Vergleich zu doppelt so schweren Paul.
1) Pauline steht zu Beginn am Baum. Dann stößt sie sich anderthalb Sekunden lang mit 40 Newton ab und rollt weiter.
- Vernachläßige zunächst die auftretende Reibung.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wieviel Impuls hat Pauline nach dem Abstoßen?
- c) Wie schnell ist sie nach dem Abstoßen?
- d) Wie weit fährt sie während des Abstoßens und wie weit in den nächsten viereinhalb Sekunden?
- e) Paul macht nun genau das gleiche wie Pauline: Er steht am Baum und stößt sich anderthalb Sekunden lang mit 40 Newton ab. Vergleiche seine Fahrt mit der von Pauline.
- f) Nimm nun an, dass bei Pauline eine Reibungskraft von 5N und bei Paul von 10N wirkt, solange sie fahren. Wie verändert sich die Fahrt der beiden?
2) Diesmal fährt Pauline zu der Zeitmessung schon mit 1 m/s am Baum vorbei und rollt weiter. Wieder soll zunächst die Reibung vernachlässigt werden.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wo ist Pauline nach 6 Sekunden und wie schnell ist sie?
- c) Begründe die Bewegungsgesetze durch die Betrachtung von Ableitungen (Steigungen) und Integralen (Flächen):
- [math]s(t) = v\, t = 2 \, \rm{\frac{m}{s}} \cdot t[/math]
- [math]v(t) = v_0 = 2\, \rm \frac{m}{s} [/math]
- [math]a(t) = 0 \, \rm \frac{m}{s^2}[/math]
- d) Löse b) mit Hilfe der Bewegungsgesetze.
3) Paul hat sich einen kleinen Motor an sein Board gebaut, der mit 20 Newton schiebt. Zu Beginn steht er am Baum.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wo und wie schnell ist Paul nach 6 Sekunden?
- c) Welche Strecke legt in der Zeitspanne von 4 bis 6 Sekunden nach Beginn der Zeitmessung zurück?
- d) Begründe die Bewegungsgesetze durch die Betrachtung von Ableitungen (Steigungen) und Integralen (Flächen):
- [math]s(t) = \frac{1}{2} \, a\, t^2 = 0{,}1 \, \rm \frac{m}{s^2} \cdot t^2[/math]
- [math]v(t) = a\, t = 0{,}2 \, \rm \frac{m}{s^2} \cdot t[/math]
- [math]a(t) = \frac{F}{m} = 0{,}2 \, \rm \frac{m}{s^2}[/math]
- e) Löse b) und c) mit Hilfe der Bewegungsgesetze.
4) Pauline kommt mit 1 m/s angerauscht. Als sie am Baum vorbeifährt, sieht sie 5 Meter vor sich "Momo", die Katze der Nachbarn, sitzen. Sie bremst ab sofort mit 15 Newton.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wie lange dauert es, bis sie steht? Schafft sie es noch vor der Katze anzuhalten? Wenn nicht, bei welcher Geschwindigkeit kollidieren die beiden?
- c) Begründe folgende Formeln für die Bremszeit und den Bremsweg:
- [math]t_{brems} = \frac{m}{F} \, v_0 [/math]
- [math]s_{brems} = \frac{1}{2}\, \frac{m}{F}\, v_0^2[/math]
- d) Wie verändert sich der Bremsweg und die Bremszeit, wenn sich die Ausgangsgeschwindigkeit verdoppelt oder halbiert?
Sprung aus der Hocke
ohne schwungholen
Sprung mit Schwungholen
Aufzug fahren
Luft- und Rollwiderstand eines Autos
Ziel ist es, die Widerstandskraft eines Autos bei verschiedenen Geschwindigkeiten zu berechnen.
Dazu wurde ein Video des Ausrollvorgangs aufgenommen, denn des während des Ausrollens wirkt nur die Widerstandskraft. Der Wagen hat laut Hersteller eine Masse von 935kg.
Das Video kann man sich hier direkt ansehen und hier als "avi" herunterladen.
Zum Anschauen des Videos ist es günstig ein Programm zu haben, bei dem man die Zeit in Sekunden angezeigt bekommt und auch von Einzelbild zu Einzelbild springen kann. Bei dem "avi"-Video geht das mit dem Programmen Avidemux oder Virtual Dub, die beide kostenlos sind.
Falls es beim Abspielen Probleme geben sollte: Der Codec des Videos heisst XVid, ist kostenlos und ist notfalls hier erhältlich.
- Erstelle anhand des Videos eine Wertetabelle und ein Diagramm der Geschwindigkeit (in m/sec) über die Zeit (in sec). Es ist sinnvoll für die Geschwindigkeiten erst eine Tabelle in km/h anzulegen und dann in m/sec umzurechnen.
t (sec) | | | | ... | | v (km/h)| 135 | 130 | 125| ... | 0 |
- Berechne daraus eine Wertetabelle und ein Diagramm der Kraft (in N) über die Zeit(in sec).
- Erstelle daraus ein Diagramm der Widerstandskraft über die Geschwindigkeit.
- Interpretiere dein Ergebnis.
Ein Fahrrad rollt bergab
Ein Fahrrad steht auf einer abschüssigen Strasse und rollt nach dem Lösen der Bremsen hinab. Die Person hat zusammen mit dem Rad eine Masse von 90kg. Für den Beginn der Bewegung ist die Reibung noch zu vernachlässigen und für den Geschwindigkeitsverlauf gilt:
- [math]v(t)= 0,8 \frac{m}{sec^2} \, t[/math]
- Zeichne die Diagramme des zeitlichen Verlaufs der ersten 10 Sekunden von Ort, Geschwindigkeit, Beschleunigung, Impuls und Kraft.
- Es sollen die Standardeinheiten verwendet werden.
- Zusatzaufgaben:
- Finde zu den Diagrammen jeweils die Funktionsgleichung (z.B. F(t)=...).
- Wieviel % Gefälle hat die Strasse?