Das Zentralfeld und die Abstandsgesetze (Gravitationsgesetz, Coulomb-Gesetz, magnetisches Coulomb-Gesetz)
Messung des magnetischen Abstandsgesetzes
Gilt [math]F \sim \frac{1}{r^2}[/math]?
- Aufbau
Schiefe Ebene, Je stärker die Neigung, desto näher sind die beiden Wagen.
Neigung:einen Meter lang, man misst die Höhe [math]x[/math].
Abstand [math]r[/math] mit Schieblehre/Zollstock.
- Messwerte und Auswertung
Die Kraft zwischen den Magneten berechnet sich als Hangabtriebskraft des Wagens:
- [math]F = m \, g \sin \alpha = m\, g \frac{x}{l}[/math]
r (cm) x (cm) F (N) 0.49 51.8 0.5076 0.55 47.2 0.4626 0.70 44.0 0.4312 0.78 39.5 0.3871 0.90 35.4 0.3469 1.00 31.8 0.3116 1.12 27.8 0.2724 1.2 24.4 0.2391 1.4 20.5 0.2009 1.6 17.6 0.1725 1.9 14.3 0.1401 2.3 11.5 0.1127 2.5 10.0 0.0980 2.7 8.3 0.0813 3.2 6.4 0.0627 3.6 4.9 0.0480 4.7 3.2 0.0314 6.5 1.6 0.0157
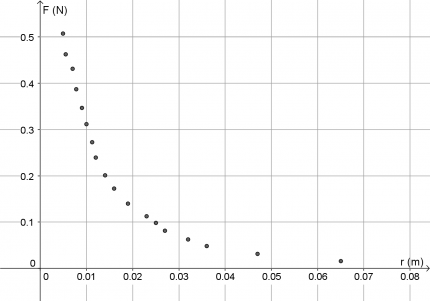
Zur Auswertung kann man erstmal die Kraft über den Abstand auftragen:
Das sieht schonmal ganz gut aus. Jetzt sollte bei einer Abstandsverdopplung sich die Kraft auf ein Viertel reduzieren. Von 0,5cm auf 1cm stimmt das nicht ganz und von 1cm auf 2cm auch nicht.
Zur genaueren Untersuchung trägt man den Kehrwert der Wurzel von F über den Abstand r auf. Dabei sollte dann eine Gerade mit der Steigung [math]\frac{1}{\sqrt a}[/math] zu sehen sein:
- [math]F = \frac{a}{r^2} \quad \Leftrightarrow \quad \sqrt F = \frac{\sqrt a}{r} \quad \Leftrightarrow \quad \frac{1}{\sqrt F} = \frac{1}{\sqrt a}\, r[/math]