Aufgaben zu den Grundlagen über Felder (Lösungen)

Fern- und Nahwirkungstheorie

1) Das Feld als Vermittler einer Wechselwirkung

„Es ist undenkbar, dass leblose, rohe Materie auf andere […] Materie wirken sollte, ohne direkten Kontakt und ohne die Vermittlung von etwas anderem, das nicht materiell ist. Dass die Gravitation eine angeborene, inhärente und wesentliche (Eigenschaft) der Materie sein soll, so dass ein Körper auf einen anderen über eine Entfernung durch Vakuum hindurch und ohne die Vermittlung von etwas Sonstigem wirken soll, […], ist für mich eine so große Absurdität, dass ich glaube, kein Mensch, der eine in philosophischen Dingen geschulte Denkfähigkeit hat, kann sich dem jemals anschließen. Gravitation muss durch einen Vermittler erzeugt werden, welcher gleichmäßig nach bestimmten Gesetzen wirkt. Aber ob dieser Vermittler materiell oder immateriell ist, habe ich der Überlegung meiner Leser überlassen.“

(Brief von Isaac Newton an Richard Bentley von 1692/1693 - in: Herbert Westren Turnbull, The correspondence of Isaac Newton 1961, Vol. III, S. 253-254)

• Wie haben wir heute dieses Dilemma gelöst?
• Welche weiteren Argumente sprechen gegen die Fernwirkungstheorie und für die Nahwirkungstheorie?

2) Formulierungen und Übersetzungen

Durch die verschiedenen Theorien hat man mindestens drei verschiedene Möglichkeiten den gleichen Sachverhalt auszudrücken:

1. als Fernwirkung
2. als Nahwirkung: "Probekörper"
3. als Nahwirkung: "aktives Feld"

• Ordne die Aussagen einer der Theorien zu:

a) Sonne und Erde ziehen sich an.

b) Die Kompassnadel richtet sich im Erdmagnetfeld aus.

c) Der geriebene Luftballon zieht die Papierschnipsel an.

d) Apfel und Erde werden zueinandergezogen.

e) Die positiv geladene Kugel und die negativ geladene Kugel ziehen sich an.

f) Das Magnetfeld zwischen Nord- und Südpol zieht die beiden Pole aufeinander zu.

• Formuliere die obigen Aussagen in allen drei Theorien.

Feldenergie

Begründen Sie möglichst anschaulich, warum ein Feld Energie enthält, indem Sie Beispiele nennen, bei denen Energie ins Feld gesteckt oder herausgeholt wird.

Graphische Darstellung von Feldern

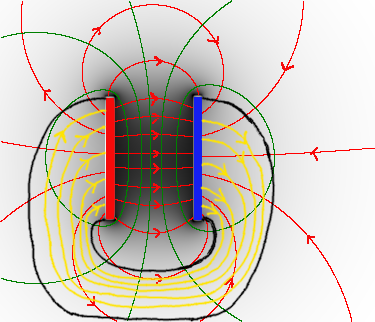
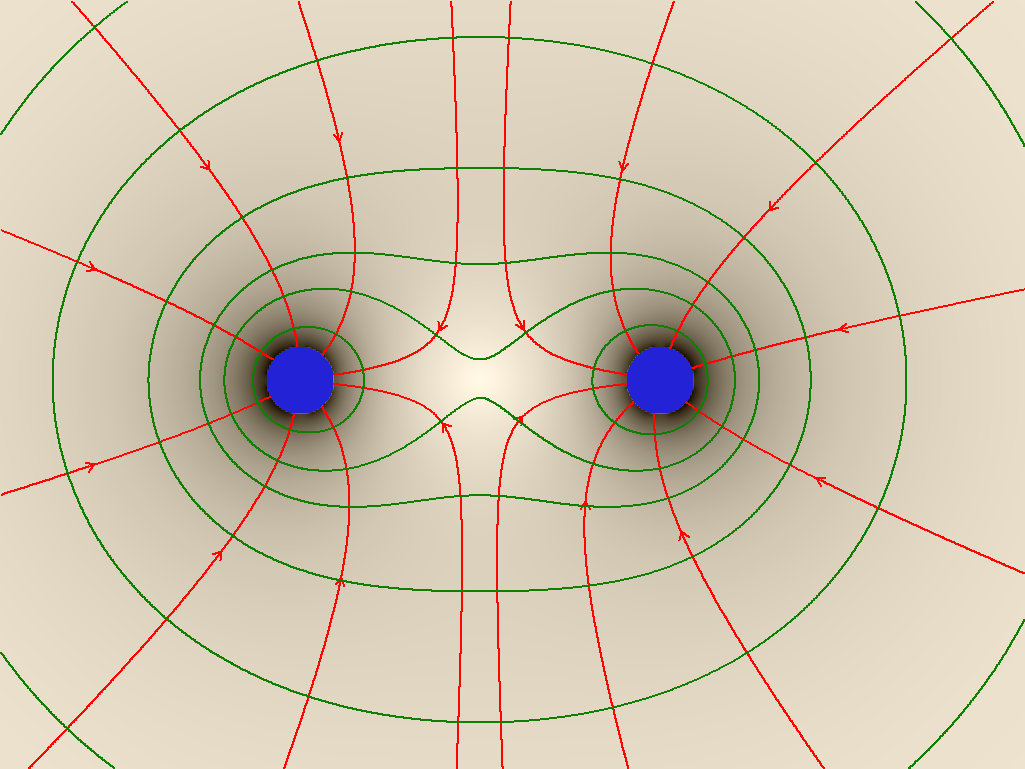
1) Drei einfache Beispiele

• Zeichnen Sie einige Feldlinien mit Pfeilen (rot) und Feldflächen (grün) ein.

a) geladene Kugel

b) Ringmagnet

c) Zwei Sonnen

• Wie kann man anhand der Feldlinien und Feldflächen die anziehende Wirkung der beiden Magnetpole und der Massen erklären?
• Zeichnen Sie in den obigen Abbidungen je einen kleinen Probekörper ein. In welche Richtung zieht/drückt ihn das Feld? (Je nach Ladung)

2) und noch mehr Felder...

• Zeichnen Sie das Feld folgender Situationen.

Erklären Sie jeweils mit Hilfe von Druck und Zugspannungen, wie das Feld zieht und drückt.

1. Ein langer Stabmagnet
2. Ein Scheibenmagnet
3. Eine "kleine" Ladung in einem homogenen Feld.
4. drei Stabmagnete aneinandergereiht
5. Erde und Mond
6. Ein Dipol mit großem und mit kleinem Abstand.
7. Ein Dipol mit ungleicher Ladungsverteilung. (Wie sieht der aus großer Entfernung aus?)

Feldstärke

1) Gravitation auf der Erde und auf anderen Himmelskörpern

a) Das Gravitationsfeld zieht die Erde und ein Kilogramm Masse mit einer Kraft von ca. 10 Newton aufeinander zu. Die Gravitationsfeldstärke beträgt daher 10 Newton pro Kilogramm: [math]g=\frac{F}{m} = 10\,\rm \frac{N}{kg}[/math]

b)Ich habe eine Masse von ca. 80kg. Meine Gewichtskraft beträgt daher auf dem Mond:

[math]F= m\, g = 80\,\rm kg \cdot 1{,}62\,\rm \frac{N}{kg} = 129{,}6\, N[/math]

c) Die vollständige Tabelle:

Planet	Feldstärke(N/kg)	Masse(kg)	Kraft(N)
Merkur	3,70	80	296
Venus	8,87	75	665
Erde	9,77	12,7	124
Mars	3,69	1000	3690
Jupiter	23	75	1725

2) Kraftwirkung im elektrischen Feld

Eine positiv geladene Kugel trägt [math]5\,\rm nC[/math] Ladung. Welche Kraft wirkt auf die Kugel in einem elektrischen Feld der Stärke [math]10\,\rm \frac{kN}{C}[/math]?

Die elektrische Feldstärke ist als Ortsfaktor, also als Kraft pro Ladung, definiert:

[math] \begin{array}{rclc} & E & = & \frac{F}{Q} \\ \Rightarrow & F & = & Q\, E \end{array}[/math]

3) Berechnung der magnetischen Ladung

Der Nordpol eines langen Stabmagneten befindet sich in einem Magnetfeld der Stärke [math]80000\,\rm\frac{N}{Wb}[/math]. Dort erfährt der Nordpol eine Kraftwirkung von [math]0{,}5\,\rm N[/math]. Wieviel magnetische Ladung trägt der Nordpol?

4) Definition der Feldstärke

Warum ist es bei der Festlegung der Feldstärke als Ortsfaktor wichtig, dass die Größe der wirkenden Kraft proportional zur Menge der Probeladung ist, also bei doppelter Probeladung auch die doppelte Kraftwirkung zu beobachten ist?

Warum ist die magnetische Feldstärke nicht mit Hilfe der Definition als Ortsfaktor praktisch messbar?

5) Tischtennisball im geladenen Kondensator

Durch eine vorhergehende Messung kennt man die elektrische Feldstärke in einem Kondensator. Sie beträgt [math]100000\,\rm \frac{N}{C}[/math]. Ein Tischtennisball mit der Masse 2,3g wird an eine 30cm lange Schnur in das Feld gehängt und elektrisch geladen. Die Schnur hängt nun nicht mehr senkrecht nach unten, sondern ist um einen Winkel von 4° ausgelenkt.

Welche Ladung trägt der Tischtennisball?

Durch das elektrische Feld zwischen den Kondensatorplatten erfährt der geladene Ball eine Kraftwirkung.

6) Das elektrische Feld der Erde

Durch den Sonnenwind, ein Strom elektrisch geladener Teilchen, und kosmische Strahlung werden negativ geladene Teilchen von der Erde weggeschleudert und die Erde positiv geladen. Bei wolkenlosen Himmel hat das dadurch enstehende elektrische Feld eine Stärke von ca. 200 N/C.

Bei Gewittern treten Feldstärken von 30000 N/C auf.

Ein kleiner Wassertropfen hat eine Masse von 0,001g. Wie muss der Tropfen geladen sein, damit er bei wolkenlosen Himmel (bei einem Gewitter) in der Luft schweben kann?

Potential

1) Potentialunterschiede am Schauinsland

Der Schauinsland im Schwarzwald hat eine Höhe von 1284 ü NHN, die Stadt Freiburg liegt am Fuße des Schauinslands auf 278 ü NHN.

a) Wieviel Energie benötigt man, um eine Wasserflasche mit 1kg Masse (einen Rucksack mit 15kg Masse) von Freiburg auf den Schauinsland zu bringen?

b) Wie groß ist die Potentialdifferenz zwischen Freiburg und dem Schauinsland?

c) Das Nullniveau der potentiellen Energie soll auf Meereshöhe liegen. Berechne das Potential des Gravitationsfeldes für Freiburg und den Schauinslandgipfel.

d) Zeichne das Gravitationsfeld oberhalb von Freiburg mit Hilfe einiger Feldlinien und den Potentialflächen von 0J/kg, 2000J/kg, 4000J/kg, ... , 14000J/kg.

2) Ein Plattenkondensator

Die beiden Platten eines Kondensators werden an eine Hochspannungsquelle von 10kV angeschlossen. Die Platten sind 20 cm x 20 cm groß und 5cm voneinander entfernt. Der Einfachheit halber gehen wir davon aus, dass sich nur zwischen den Platten ein elektrisches Feld befindet, welches deshalb auch homogen ist.

a,b,e)

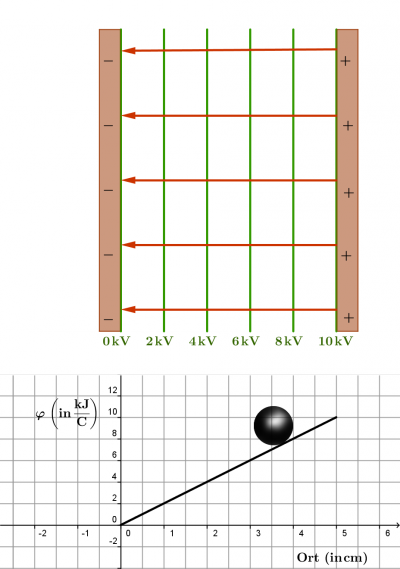
c) Wie groß ist die Stärke des elektrischen Feldes zwischen den Platten?

[math]E=\frac{\triangle\varphi}{\triangle s}=\rm \frac{10\, kV}{0{,}05\, m}=200000\frac{V}{m}=200000\frac{N}{C}[/math]

d) Ein Tischtennisball wird an einem sehr langen Faden in das Feld gehängt. Durch den langen Faden wird der Ball bei einer Auslenkung aus der Ruhelage kaum angehoben. Welche Art von Bewegung vollzieht er, wenn man ihn kurz mit der positiv geladenen Platte in Berührung bringt?

Der Ball wird immer schneller, er bekommt Energie aus dem Feld.

e) Vergleichen Sie die Bewegung mit dem Rollen einer Kugel im Potential.

Im Modell rollt der Ball die schiefe Potentialebene hinunter. Die potentielle Energie sinkt, die kinetische Energie steigt an.

f) Wieviel Energie würde ein mit +1C geladener Ball (ein Elektron) erfahren, dass sich von der positiven zur negativen Platte bewegt?

[math]\varphi=\frac{W}{Q}[/math]

[math]\Rightarrow W_{\rm Ball} = Q\,\varphi = \rm 1\, C \cdot 10\rm \frac{kJ}{C} = 10\,kJ[/math]

[math]\Rightarrow W_e = Q\,\varphi = \rm 1{,}6\cdot10^{-19} C \cdot 10\frac{kJ}{C} = 1{,}6\cdot 10^{-15} J[/math]

g) Wie schnell wäre er (das Elektron) an der negativen (positiven) Platte?

An der negativen Platte ist die gesamte potentielle Energie in kinetische Energie gewandelt worden:

[math]W_{\rm kin}=\frac{1}{2}\,m\,v^2[/math]

[math]\Rightarrow v_{\rm Ball}=\sqrt{\frac{2\, W}{m}}= \sqrt{\frac{2\cdot 10\,\rm kJ}{0,002\,\rm kg}}=3160\rm \frac{m}{s}\approx 11400 \rm \frac{km}{h}[/math]

Das ist unrealistisch schnell und liegt daran, dass man einen Tischtennisball normalerweise nur mit ca 10nC laden kann!

[math]\Rightarrow v_e=\sqrt{\frac{2\, W}{m}}= \sqrt{\frac{2\cdot 1{,}6\cdot 10^{-15} \rm J}{9{,}1\cdot 10^{-31}\rm kg}}= 59300000\frac{m}{s}[/math]

Das Elektron kann tatsächlich auf so eine hohe Geschwindigkeit beschleunigt werden! Das sind ca. 20% der Lichtgeschwindigkeit von 300000 km/s.

3) Eine Batterie

Ein geladener Akku hat eine Spannung von 1,2V. Der Akku wird mit einem 1m langem Kabel kurzgeschlossen, wodurch das Kabel erwärmt wird. (Der Einfachheit halber nehmen wir an, dass die Spannung dabei zeitlich konstant ist.)

a) Wieviel Energie erhält ein Elektron von der Batterie, wenn es vom Minuspol bis zum Pluspol geschoben wird?

b) Wie groß ist die Feldstärke im Kabel?

c) Welche Kraft wirkt auf das Elektron?

d) Auf dem Akku steht "2000mAh". Das bedeutet, dass er bis er "leer" ist, also keine Energie mehr enthält, eine elektrische Ladungsmenge von 2C durch das Kabel schiebt.

Wieviel Energie kann der Akku speichern?

4) Ein Satellit im Schwerefeld der Erde

• Wieviel Energie benötigt man, um den Satellit (Masse 800 kg) an die markierte Stelle zu heben?
• Welche Kraft wirkt dort ungefähr auf ihn?

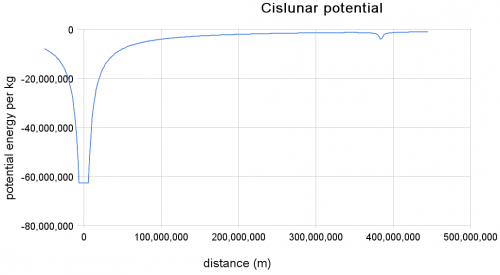
5) Mondstation

• Wieviel Energie benötigt man, damit man 1 Tonne Nachschub-Material auf eine Mondstation bringen kann?
• Wieviel potentielle Energie hat das Material dann auf der Mondoberfläche?
• Vergleichen Sie die Energiemengen mit Benzinmengen! (Ein Kilogramm Benzin enthält ca. 43 MJ Energie, ein Liter Benzin 35 MJ.)

Potential der Erde

Anton steht auf der Erde. Bertha befindet sich einen Erdradius oberhalb der Erdoberfläche in einer Raumkapsel. Cecilie ist zwei Erdradien von der Erde entfernt. (usw.)

• Berechnen Sie die Potentialunterschiede zwischen A und B, B und C, ...
• Berechnen Sie das Potential an den Stellen A, B, C, ...

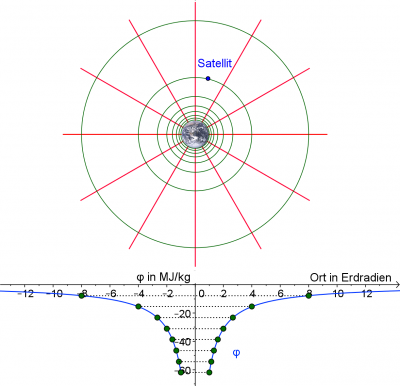
Geostationärer Satellit

Ein Satellit (Masse 800 kg) soll in eine geostationäre Umlaufbahn, also in eine Höhe von etwa 36.000 km über der Erdoberfläche. Der Bahnradius beträgt dann ungefähr 42.000 km.

• Berechnen Sie mit Hilfe einer Gleichung für die Feldstärke oder des Potential die dazu nötige Energiemenge.
• Vergleichen Sie die Energiemengen mit Benzinmengen! (Ein Liter Benzin enthält ca. 42 MJ Energie.)

Schwere, Elektrische und Magnetische Wechselwirkung (Gravitation, Elektrostatik, Magnetostatik)

Versuche beschreiben und erklären mit der Nahwirkungstheorie.

Segnersches Rad, "Wedelgenerator", ...

Ladung als Quellenstärke und der Fluß eines Feldes

Masse der Erde

• Wieviel (schwere) Masse hat die Erde?

Der Feldfluss durch die Erdoberfläche ist genauso groß wie die Erdmasse:

[math]\frac{1}{4\pi \,G} \ g \, A = m[/math]

Jetzt muss man nur die Fläche zu [math]A= 4 \pi \, r^2[/math] und die Gravitationskonstante einsetzen:

[math]\frac{1}{4\pi \,6{,}673\;84\; \cdot 10^{-11} \mathrm{\frac{m^3}{kg \cdot s^2}}} \ 9{,}81 \rm \frac{N}{kg} \, 4 \pi \, (\rm 6380000 m)^2 \approx 5{,}987 \cdot 10^{24}\rm kg[/math]

Das ist schon ein recht vernünftiger Wert im Vergleich zu genaueren Messwerten.

Gravitationsfeldstärke im All

• Wie groß ist die Gravitationsfeldstärke in einem Abstand von 3680 km über dem Erdboden?

Mit Erdmasse

In einem Abstand von 3680 km über dem Erdboden ist man 7360 km vom Ermittelpunkt entfernt. Man betrachtet den Feldfluss durch eine Kugeloberfläche mit diesem Radius. Dazu kann man die Formel für die Quellenstärke umformen:

[math]g = 4 \pi \, G\, \frac{m}{A} = 4 \pi \, 6{,}673\;84\; \cdot 10^{-11} \mathrm{\frac{m^3}{kg \cdot s^2}}} \, \frac{5{,}987 \cdot 10^{24}\rm kg}{4 \pi \, (7360000 m)^2} \approx 2{,}45 \rm \frac{N}{kg}[/math]

Verdopplung der Entfernung

Durch den doppelten Abstand vom Erdmittelpunkt vergößert sich die Kugelfläche auf das Vierfache. Denn der Radius wird quadriert: [math]A=4 \pi \, r^2[/math]

Da der Fluss durch die Fläche aber gleich bleibt muss die Feldstärke auf ein Viertel abnehmen!

[math]g = \frac{1}{4} \, 9{,}81 \frac{N}{kg} = 2{,}45 \frac{N}{kg}[/math]

• Welche Kraft wirkt dort auf einen 1000kg schweren Satelliten?

Die Feldstärke ist der Ortsfaktor:

[math]g=\frac{F}{m} \qquad \Rightarrow \qquad F = m \, g = 1000 \rm kg \cdot 2{,}45 \frac{N}{kg} = 2450 \, N[/math]

Gravitation in der Erdkugel

• Wie groß ist die Stärke des Schwerefeldes innerhalb der Erdkugel?

Man betrachtet eine Kugeloberfläche mit dem Radius r. Damit läßt sich die Feldstärke im Abstand r vom Erdmittelpunkt berechnen.

Dazu nehmen wir vereinfachend an, dass die Erde überall die gleiche Massendichte [math]\rho[/math] hat.

Nun ist der Fluss aus der Fläche gleich der enthaltenen Masse. Die Masse ausserhalb der Kugel spielt keine Rolle! Das ist erstaunlich. Die Wirkung der Kugelschale ausserhalb der Kugel hebt sich gerade auf. (Vgl. Wikipedia: Kugelschale.)

[math]\frac{1}{4 \pi \, G} \, g \, A = m \qquad \Rightarrow \qquad g = 4 \pi \, G \, \frac{m}{A} = 4 \pi \, G \, \frac{V \, \rho}{A}\qquad .[/math]( mit [math]m= V\, \rho[/math])

Jetzt sieht man, dass es auf das Verhältnis von der enthaltenen Masse, bzw. des Kugelvolumens, zur Oberfläche der Kugel ankommt! Mit [math]A= 4 \, \pi r^2[/math] und [math] V= \frac{4}{3} \, \pi \, r^3[/math] ergibt sich:

[math]g = 4 \pi \, G \, \frac{\frac{4}{3} \, \pi \, r^3 \, \rho}{4 \, \pi r^2} \qquad \Rightarrow \qquad g = \frac{4}{3}\pi G \rho \ r[/math]

Die Feldstärke ist also proportional zum Abstand des Erdmittelpunktes! Sie nimmt linear zu. Das liegt daran, dass das Volumen in der dritten Potenz zum Radius größer wird, die Oberfläche in der zweiten Potenz.

Realistischerer Verlauf der inneren Feldstärke nach genauerern Modellen. (Wikipedia: Preliminary Reference Earth Model)

Probekörper im Kondensator

Zwei geladene Platten, je 30cm x 30cm groß, eine mit 8 10^-8 C, die andere mit -8 10^-8 C.

• Bestimmen Sie die Stärke des elektrischen Feldes unter der Annahme, dass das Feld sich ausschließlich zwischen den Platten befindet und dort homogen ist.
• Warum ist dabei die Feldstärke zwischen den Platten nicht vom Abstand der Platten abhängig?

Zwischen die Platten wird ein negativ geladener Tischtennisball gehängt. Auf ihn wirkt eine Kraft von 0,01 N.

• In welche Richtung wird der Ball gezogen?
• Wieviel Ladung sitzt auf dem Ball?