Das Konzept der Energie (Energieträger und Potential)
(Kursstufe > Theoretisch-deduktives Vorgehen am Beispiel der Energie)
Inhaltsverzeichnis
- 1 Einführung und Beispiele
- 2 Systemisches Denken
- 3 Zusammenfassung: Energie, ihre Träger und das Potential
- 4 Berechnung der Energiemengen
- 5 Literatur
- 6 Links
- 7 Fußnoten
Einführung und Beispiele
Womit Menschen ihre Energie beziehen können. (Video: Wieviel Energie steckt in einem Brötchen?
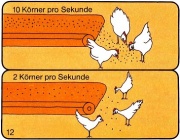
Auch hier bekommt nicht jedes Huhn die gleiche Energiemenge. (Aus dem Energiebuch des Schroedel Verlags)
Energiemenge eines Wassergefüllten Glases
- Es gibt verschiedene Energieträger (Energieformen):
- warme Gegenstände: Entropie (thermische Energie)
- zusammengedrückte oder auseinandergezogene Gegenstände: Druckluft, mechanische Feder (Spannenergie)
- hochgehobene Gegenstände: Schwerefeld (Lageenergie)
- sich bewegende Gegenstände: Impuls (Bewegungsenergie)
- Bei einigen Energieträgern ist die enthaltene Energiemenge vom Bezugssystem abhängig:
- Schwerefeld (Lageenergie)
- Impuls (Bewegungsenergie)
Systemisches Denken
Beschreibung eines Zustandes
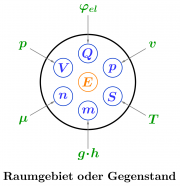
Ein Gegenstand wird einerseits durch die Angabe der enthaltenen Mengen von bestimmten Größen beschrieben.
Weiterhin kann man an jeder Stelle des Gegenstands bestimmte Eigenschaften durch die Messung von ortsgebundenen Größen beschreiben.
Mit Ausnahme der Energie kann jeder extensiven, mengenartigen Größe eine intensive, ortsgebundene Größe zugeordnet werden.
| Mengenartige (extensive) Größen | haben zugehörige Eigenschaften (intensive Größen), welche man Potential nennt. | ||
|---|---|---|---|
| Energiemenge [math]E[/math] | in [math]\mathrm{J}\, \text{(Joule)}[/math] | ||
| el. Ladung [math]Q[/math] | in [math]\mathrm{C }\text{(Coulomb)}[/math] | el. Potential [math]\varphi_{el}[/math] | in [math]\mathrm{V}\, \text{(Volt)} = \rm \frac{J}{C}[/math] |
| Impuls [math]p[/math] | in [math]\mathrm{Hy} \, \text{(Huygens)} = \rm kg \frac{m}{s}[/math] | Geschwindigkeit [math]v[/math] | in [math]\mathrm{\frac{m}{s} = \frac{J}{Hy} }[/math] |
| Entropiemenge [math]S[/math] | in [math]\mathrm{Ct}\, \text{(Carnot)} = \rm \frac{J}{K}[/math] | absolute Temperatur [math]T[/math] | in [math]\mathrm{K}\, \text{(Kelvin)} = \rm \frac{J}{Ct}[/math] |
| Masse [math]m[/math] | in [math]\mathrm{kg}[/math] | Schwerepotential [math]gh[/math] | in [math]\mathrm{\frac{m^2}{s^2} = \frac{J}{kg}}[/math] |
| Stoffmenge [math]n[/math] | in [math]\mathrm{mol}[/math] | chem. Potential [math]\mu[/math] (freie molare Standardenthalpie) |
in [math]\mathrm{\frac{J}{mol} }[/math] |
| Volumen [math]V[/math] | in [math]\mathrm{m^3}[/math] | Druck [math]p[/math] | in [math]\mathrm{Pa} \, \text{(Pascal)} = \mathrm{10^{-5}bar = \frac{J}{m^3} }[/math] |
Systemveränderungen
- Verändert sich die Energiemenge, so verändert sich auch immer noch eine andere mengenartige Größe, der sogenannte Energieträger!
- Bei einigen physikalischen Phänomenen hat man lange und intensiv gestritten, ob die Energie oder der Energieträger die "wichtigere" physikalische Größe sei.
- In der Mechanik ging der Streit darum, ob die Größe [math]m\, v[/math], also der Impuls, oder [math]m\, v^2[/math], die halbe Bewegungsenergie, denn die richtige Größe zur Beschreibung von Bewegungen ist.
- In der Wärmelehre bezeichnete Sadi Carnot zunächst noch mit Wärme, was wir heute Entropie nennen. Unter Wärme wird heute eine Energiemenge verstanden.[1]
- Offensichtlich ist es nicht sinnvoll sich über die "Wichtigkeit" von Größen Gedanken zu machen. Wesentlich ist die Erkenntnis, dass an Energietransport- und Umwandlungsprozessen immer zwei Größen beteiligt sind und dass man sie voneinander unterscheidet.
 Auch hier bekommt nicht jedes Huhn die gleiche Energiemenge pro Zeit. (Aus dem Energiebuch des Schroedel Verlags) |
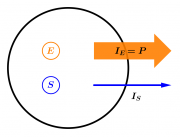
- Die Stärke des Energiestroms [math]I_E[/math] (oder auch Leistung [math]P[/math]) ist proportional zur Stärke des Trägerstroms [math]I_{Tr\ddot ager}[/math]. Das Potential [math]\varphi[/math] ist gerade die Proportionalitätskonstante und gibt an, wie stark der Träger mit Energie beladen ist:
- [math]I_E = P = \varphi \, I_{Tr\ddot ager}[/math]
- Für kleine Zeitspannen oder konstantes Potential kann man das auch so schreiben:
- [math]\frac{Energie}{Zeit} = \frac{Energie}{Tr\ddot agermenge} \cdot \frac{Tr\ddot agermenge}{Zeit}= Potential \cdot \frac{Tr\ddot agermenge}{Zeit}[/math]
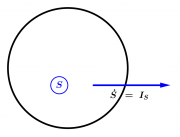
- Die Stärke des Energiestroms kann man auch als zeitliche Änderungsrate der Energie interpretieren. Die Energiemenge des Gebietes ändert sich genau so, wie die Stromstärke angibt. Fließt die Energie heraus, ist die Änderungsrate der Energie negativ, fließt die Energie hinein, ist die Änderungsrate positiv. Die zeitliche Ableitung einer Größe notiert man mit einem Punkt über dem Symbol. Zum Beispiel gilt für die Wärmeenergie:
- [math]\dot E = P = T \, \dot S[/math]
- Eine weitere Schreibweise ist die Angabe der absoluten Änderungen. Schreibt man die Änderungsrate als Quotient für eine "kleine" Zeitspanne [math]\triangle t[/math], so kann man mit der Zeitspanne multiplizieren. Für eine kleine Zeitspanne oder ein konstantes Potential gilt also:
- [math]Energie = Potential \cdot Tr\ddot agermenge[/math]
- Und speziell für die Wärmeenergie:
- [math]\dot E = \frac{\triangle E}{\triangle t} = T \, \frac{\triangle S}{\triangle t} \quad \Rightarrow \quad \triangle E = T \, \triangle S \qquad \text{ } [/math] (Gilt nur für annähernd konstante Temperatur T!)
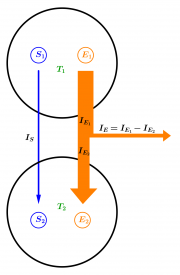
- In der Regel strömt aber der Energieträger von einem Gebiet in ein anderes. Sind die Potentiale unterschiedlich, gibt es einen Netto-Energiestrom von den beiden Systemen weg. Für die Leistung dieses Nettoenergiestroms gilt:
- [math]\begin{array}{rcl} P=I_E &=&I_{E_1}-I_{E_2} \\ &=&T_1\, I_S - T_2\, I_S = (T_1-T_2)\, I_S\\ &=&\Delta T \, I_S \\ \end{array} [/math]
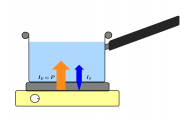
Beispiel: Von dem warmen Wasser über das Peltierelement in das kalte Wasser fließt ein Entropiestrom, den man zunächst vereinfachend als konstant ansehen kann. Es kommt weniger Energie an, als wegfließt, weil die Temperatur und damit die Beladung des Entropiestromes abnimmt. Die Energie ist auf die elektrische Ladung umgeladen worden, welche dann wiederum im Motor auf die Bewegung (den Impuls) umgeladen wird.
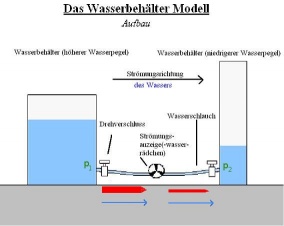
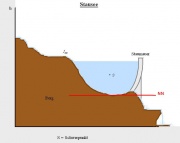
Das Wasserbehältermodell
- Wassermenge und Stromstärke (Durchsatz)
- Wasserhöhe und Druck
- Widerstandskonzept:
- Druckunterschied als Antrieb
- Stömungswiderstand
- Energietransportkonzept:
- Druck als Energiebeladungsmaß
- Druckunterschied als Potentialdifferenz
- Energiestromgleichung (Leistung) [math]P=\triangle p I_W \qquad \qquad \dot E = \triangle p \dot W [/math]
Das Wasserbehältermodell besteht aus zwei, mit unterschiedlich viel Wasser gefüllten, Zylindern.
Sobald man die Drehverschlüsse an beiden Seiten aufgedreht, strömt das Wasser aus dem höher mit Wasser gefüllten Bottich in den Zweiten.
Dieser Vorgang lässt sich mit Hilfe des Wasserrädchens beobachten und stoppt erst, nachdem die Wasserpegel beider Seiten sich auf ein gleiches Niveau begeben haben.
Antrieb-Widerstand-Konzept
Die Strömung entsteht durch den vonstatten gehenden Druckausgleich, der durch die unterschiedlichen Druckverhältnisse in den Gefäßen verursacht wird. Die Druckdifferenz zwischen dem Zylinder mit dem höheren und dem niedrigeren Wasserpegel, ist der Antrieb. Ein Widerstand besteht durch die Reibung in der Wasserleitung und dem Wasserrädchen, dadurch fließt das Wasser nur langsam in den anderen Behälter.
Den Widerstand einer Wasserleitung legt man als Quotient von Antrieb und Stromstärke fest:
- [math]R = \frac{\Delta p}{I} \quad \Leftrightarrow \quad I = \frac{1}{R}\, \Delta p[/math]
Die Stromstärke ist zum Antrieb, also dem Druckunterschied proportional. Der Kehrwert des Widerstandes ist die "Leitfähigkeit" der Leitung.
Das ist auch auf andere Energieträger übertragbar, wie den elektrischen Widerstand und die elektrische Leitfähigkeit:
- [math]R = \frac{\Delta \varphi}{I}= \frac{U}{I} \quad \Leftrightarrow \quad I = \frac{1}{R}\, U[/math]
Energieträger-Potential-Konzept
Das Wasser ist der Energieträger, der auf der Seite mit dem höheren Wasserpegel, auf Grund des höheren Drucks mit mehr Energie beladen ist. Sobald eine Verbindung zwischen den beiden Behältern gegeben ist, versuchen die unterschiedlichen Energiepegel (Potentiale) sich auf beiden Seiten auszugleichen. Ein Teil der Druckenergie wird „auf dem Weg“ zur anderen Seite auf einen anderen Energieträger umgeladen. Es entsteht durch die Reibung nämlich Entropie.
Zusammenfassung: Energie, ihre Träger und das Potential
- Energie ist das Geld der Physik. Man kann damit ausdrücken, wieviel etwas wert ist.
- Es ist alles andere als selbstverständlich, daß wirklich sämtliche Situationen vergleichbar und in einer Einheit auch bewertbar sind.
- Energie kann in verschiedenen Trägern gespeichert werden: Bewegung, Wärme, Benzin, Licht, Elektrizität,...
- Allen Energieträgern entspricht auch eine physikalische, mengenartige Größe. Den Mengencharakter erkennt man gut bei einer Verdoppelung des Gegenstands. So haben zwei identische Pferde die doppelte Masse, Impuls, Volumen, Entropie, Ladung, Stoffmenge.
- Manche Energieträger sind "teurer" als andere. So enthält Benzin mehr Energie als die gleiche Menge Kohle.
- Der "Kilo-Preis", also die Energiemenge pro Trägermenge wird Potential (o. Beladungsmaß) genannt. Die Potentiale sind physikalische Größen, die punktuelle Eigenschaften des Trägers beschreiben. Bei einer Verdoppelung des Gegenstandes bleiben sie unverändert: So haben zwei identische Pferde die gleiche Geschwindigkeit, Temperatur, Druck, Brennwert,...
- Bei den meisten Energieträgern kann das Potential sich verändern, die "Preise" müssen also nicht konstant sein!:
- Viele Vorgänge in Natur und Technik lassen sich als Wechsel der Energie von einem Träger zu einem anderen beschreiben.
- Bei brennender Kohle von der Kohle in die Wärme der Flamme, bei einem laufenden Menschen von der Nahrung in die Bewegung, bei einem Elektromotor von der Elektrizität in die Bewegung, bei der Photosynthese vom Licht in Kohlehydrate,...
- Bei allen Vorgängen bleibt der Wert, also die Energiemenge, immer gleichgroß:
- Energie ist eine Erhaltungsgröße, sie kann weder erzeugt, noch vernichtet werden. (Im Gegensatz zum Geld gibt es auch weder Inflation noch Deflation :)
- Die Energieträger Ladung, Impuls, Masse und Stoffmenge sind auch Erhaltungsgrößen, die Entropie dagegen nicht.
- In der Regel ist die absolute Energiemenge eines Trägers uninteressant. Man interessiert sich viel mehr für die Energiemengen, die während eines Vorgangs hinaus- oder hineingehen.
- Kocht man Wasser, so ist es interessant zu wissen, wieviel Energie man braucht, um es von Zimmertemperatur auf 100°C zu erhitzen. Die absolute Energiemenge, die man braucht, um Wasser von 0K (-273,15°C) auf 373,15K (100°C) zu erwärmen ist von theoretischem Interesse, für das Wasserkochen aber nicht relevant.
- Die Veränderungen der Energiemenge kann man durch einen Energieträgerstrom beschreiben, der die Energie rein oder raustransportiert.
- Um eine gespeicherte Energiemenge zu bestimmen, muss man den heraus- oder hereinfließenden Energiestrom integrieren.
- Es ist (leider!?) auch üblich der gespeicherten Energie einen anderen Namen zu geben als der Energie, welche transportiert wird. Man nennt die gespeicherte Energie eine Zustandsgröße, die strömende eine Prozessgröße. (In der Chemie werden bestimmte Energiemengen auch als Enthalpie bezeichnet.)
Zustandsgröße Prozessgröße mechanische Energie mechanische Arbeit thermische Energie Wärme
Tabelle
| Name der Energie | Mengenartige (extensive) Größen (Energieträger) |
haben zugehörige Eigenschaften (intensive Größen) (Potential / Beladungsmaß) |
Leistung [math]P = \dot E[/math] |
absolute Energieänderung |
gespeicherte Energie | ||
| Energie | [math][E]=\mathrm{J \quad(Joule)}[/math] | ||||||
| elektrische Energie | el. Ladung | [math][Q] = \mathrm{C \quad (Coulomb)}[/math] | el. Potential | [math][\varphi_{el}] = \mathrm{V \quad (Volt)}=\rm \frac{J}{C}[/math] | [math]P=\varphi \, I \quad (U\, I)[/math] | [math]\triangle E = \varphi \, Q \quad (U \, Q)[/math] | [math]E= \bar \varphi \, Q \quad (\bar U \, Q)[/math] |
| Bewegungsenergie | Impuls | [math][p] = \mathrm{Hy \quad (Huygens)= kg \frac{m}{s}} [/math] | Geschwindigkeit | [math][v] = \mathrm{m/s} =\rm \frac{J}{Hy}[/math] | [math]P=v \, \dot p = v \, F[/math] | [math]\triangle E = v \, \triangle p[/math] | [math]E = \bar v \, p = \frac{1}{2}\, m\, v^2[/math] |
| Wärmeenergie | Entropie | [math][S] = \mathrm{Ct \quad (Carnot) =\frac{J}{K}}[/math] | absolute Temperatur | [math][T] = \mathrm{K \quad (Kelvin)} =\rm \frac{J}{Ct}[/math] | [math]P=T \, \dot S[/math] | [math]\triangle E = T \, \triangle S[/math] | [math]E= \bar T \, S[/math] |
| Lageenergie | Masse | [math][m] = \mathrm{kg}[/math] | Schwerepotential | [math][gh] = \mathrm{m^2/{s^2} }=\rm \frac{J}{kg}[/math] | [math]P= gh\, \dot m[/math] | [math]\triangle E = gh \, \triangle m[/math] | [math]E = g\bar h \, m[/math] |
| chemische Energie | Stoffmenge | [math][n] = \mathrm{mol}[/math] | chem. Potential | [math][\mu] = \mathrm{\frac{J}{mol} }[/math] | [math]P= \mu \, \dot n[/math] | [math]\triangle E = \mu \, \triangle n[/math] | [math]E = \bar \mu \, n[/math] |
| Druckenergie | Volumen | [math][V] = \mathrm{m^3}[/math] | Druck | [math][p] = \mathrm{Pa \quad (Pascal) }[/math] [math]\text{} \quad \ \, \mathrm{= 10^{-5}bar =\frac{J}{m^3} }[/math] |
gilt nur für (z.B. für [math]P= p\, \dot V[/math] |
adiabatische[2] inkompressible [math]\triangle E = p \, \triangle V[/math] |
Vorgänge! Flüssigkeiten) [math]E = \bar p \, V[/math] |
Berechnung der Energiemengen
Bei konstantem Beladungsmaß (Potential)
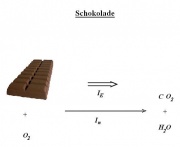
Schokolade
Trägergröße: Stoffmenge n (mol)
Potential: chem. Potenzial μ (J/mol)
oder
Trägergröße: Masse m (kg)
Potential: chem. Potential [math]\mu [/math] (J/kg)
- [math]I_E=I_n \, \mu[/math] (oder: [math]\dot E=\dot n \, \mu[/math])
Bei der Änderung der Schokoladenstoffmenge ändert sich das chemische Potential nicht. Deswegen gilt hier:
- [math]E=n \, \mu[/math]
Beispiel Bei einer Tafel Schokolade steht auf der Packung: Brennwert pro 100g: 2570 kJ.
Das bedeutet, dass ihr chemisches Potential [math]\mu =25700 \,\rm \frac{kJ}{kg} \approx 26\,\rm \frac{MJ}{kg}[/math]beträgt.
Bei einer Masse von 200g ergibt sich:
[math]E= 0,2 kg \cdot 25700 \,\rm \frac{kJ}{kg} = 5140\,\rm kJ \approx 5\,\rm MJ[/math]
Atombombe
Trägergröße: Masse m (kg)
Potential: [math]c^2[/math] (J/kg)
- [math]I_E=I_m \, c^2[/math]
Auch bei einer Atombombe ist das Beladungsmaß konstant, es gilt nämlich die berühmte Formel:
- [math]E= m \, c^2[/math]
Das heißt, die Masse der Atomkerne ist die Trägergröße und wenn diese sich bei der Kettenreaktion verkleinert, so speichern die Kerne weniger Energie.
Der Faktor [math]c^2[/math] gibt an, wie stark die Masse mit Energie beladen ist, nämlich mit [math]299792458^2 \,\rm \frac{J}{kg} \approx 9 \cdot 10^{16}\rm \frac{J}{kg} = 90000000 \,\rm \frac{MJ}{kg}[/math]. Das ist eine ganze Menge!
Benzin
Zum Vergleich: Benzin hat ein chemisches Potential von ca. [math]40 \,\rm \frac{MJ}{kg}[/math].
Energieübertragung bei Fließgleichgewicht
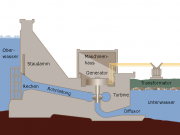
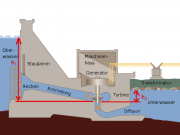
Ein Wasserkraftwerk versorgt Haushalte und Industrie mit Strom. Es benutzt die Energie, die im aufgestauten Wasser enthalten ist, um den elektrischen Strom anzutreiben.
Genauer wird die Energie vom Wasser auf die bewegte Turbine und die Generatorwelle umgeladen. Danach wird im Generator die Energie von der Bewegung auf die Elektrizität umgeladen.
Während das Kraftwerk läuft, fließt ein konstanter Energiestrom vom Wasser bis in die elektrische Ladung.
Ebenso sind die Ströme und die Mengen der Energieträger zeitlich konstant: Die Wassermenge des Sees bleibt unverändert, denn es soll genausoviel Wasser nachfließen wie wegfließt. Der Wasserstrom durch die Turbine ist konstant. Der Impuls der Turbine ist auch konstant, denn es fließt genausoviel Impuls hinein, wie heraus. (Oder, anders ausgedrückt, die antreibende und die bremsende Kraft ist gleichgroß.) Ebenso ist der elektrische Strom durch den Generator konstant. Daher spricht man von einem Fließgleichgewicht.
Bei jeder Umladung verändert sich das Beladungsmaß des Energieträgers: Zunächst nimmt der Druck des Wassers stark ab, was anzeigt, dass das Wasser seine Energie abgibt. Diese Energie wird genutzt, um Impuls von der Erde auf das Turbinenrad zu übertragen. Die Geschwindigkeit des Impulses nimmt zu. Durch den Generator wird die Turbine gebremst, der Impuls kommt wieder auf ein niedriges Geschwindigkeitsniveau, und andererseits wird die elektrische Ladung von einem niedrigen Potential auf ein hohes angehoben. Wird nun vom Strom eine Lampe betrieben, so fällt das elektrische Potential hinter der Lampe wieder ab. Die Ladung hat ihre Energie wieder abgegeben, in diesem Fall mit dem Licht und der Entropie.
(Bemerkung: In der Umgangssprache heißen die großen Energie"lieferanten", welche den Strom aus der Steckdose fließen lassen aus historischen Gründen "Kraftwerke", obwohl sie uns gar keine Kraft im physikalischen Sinne liefern.)
Wasserkraftwerk
Träger: Schwerefeld, Masse m
Potential: gh
- [math]I_E=I_m \, g\, h[/math] (oder [math]\dot E=\dot m \, g\, h[/math])
oder
Träger: Volumen (Kubikmeter)
Potential: Druck (Pascal)
- [math]I_E=I_V \, p[/math] (oder [math]\dot E=\dot V \, p[/math])
Fließt der Massestrom bei einer konstanten Wasserhöhe in die Turbine, so ist das Potential (sowohl die Höhe als auch der Druck) konstant.
Das Wasser mit der Masse m fügt der Turbine die Energie m*gh zu. Wobei h die "Fallhöhe" der Turbine, also die Höhendifferenz von Ober- und Unterwasser ist.
- [math]E=m\, g\, h[/math]
Das Wasser mit dem Volumen V fügt der Turbine die Energie V p zu. Wobei p die Druckdifferenz des Wassers vor und nach der Turbine ist.
- [math]E=V\, p[/math]
Beispiele
|
An einem Wasserkraftwerk an der Dreisam finden sich folgende Angaben:
Man kann aus Durchfluss und Fallhöhe die maximale Leistung berechnen:
Die Turbine hätte demnach einen sehr hohen Wirkungsgrad! |
Aus der Wikipediaseite über das Schluchseewerk kann man Angaben zur Oberstufe bei Häusern entnehmen:
- Fallhöhe: 200 m
- Leistung 100 MW
Daraus läßt sich die Stärke des Wasserstroms berechnen:
Es gilt für die Druckdifferenz: [math]p \approx 20\,\rm bar = 2.000.000\,\rm Pa[/math]
Wegen [math]\text{} \quad I_E = I_V \, p \quad\text{}[/math] folgt [math]\text{} \quad I_V=\frac{I_E}{p} = \frac{100\,\rm MW}{2\,\rm MPa} = 50 \frac{\,\rm m^3}{\,\rm s}[/math]
Der Wasserstrom wird sogar noch stärker sein, wegen der auftretenden Verluste.
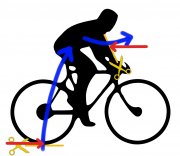
Fahrrad fahren
Träger: Impuls [math]p[/math]
Potential: Geschwindigkeit [math]v[/math]
- [math]I_E=I_p \, v \quad \text{}[/math] (oder [math]\dot E=\dot p\, v [/math] oder [math]P=F\, v[/math])
Nach dem 2. Newtonschen Axiom gibt die Kraft die zeitliche Änderung des Impulses an. Bei konstanter Geschwindigkeit ist die Antriebskraft entgegengesetzt gleichgroß der Widerstandskraft. Es fließt also genausoviel Impuls aus der Erde ins Rad wie, wegen der Luftreibung, hinaus in die Luft und, wegen der Reibung am Boden, zurück in die Erde. (Vgl. dieses Beispiel)
Beispiel Ein Radfahrer fährt konstant mit 36 km/h und gleicht dabei einen Widerstand der Stärke 12 Newton aus. Es fließen also pro Sekunde 12 Huygens Impuls durch den Radfahrer. Durch sein Treten wird der Impuls auf das hohe Geschwindigkeitsniveau gebracht. Dann fließt der Impuls wieder auf das niedrige Niveau zurück, womit dem Radfahrer Energie verloren geht.
- Der Energiedurchsatz oder die Leistung beträgt: [math]I_E = F\, v = 10 \,\rm N \cdot 10 \rm \frac{m}{s} = 120 \rm\frac{J}{s}[/math]
Der Radfahrer strampelt also mit 120 Watt, hauptsächlich um die Luft "anzuschieben".
Energiebedarf eines Hauses mit Ölheizung und Wärmepumpe
Ein Haus, das mit einer Ölheizung auf eine Temperatur von 25°C geheizt wird, hat einen Energiebedarf von 9000 Watt.
Wie groß ist der Wärmeverlust des Hauses?
Berechnung:
- [math]25^\circ \,\rm C = 298{,}2 \,\rm K[/math]
- [math]I_E=I_S \, T [/math]
- [math]\Rightarrow I_S = \frac{I_E}{T} =\frac{9000\,\rm W}{298{,}2 \,\rm K} = 30{,}2\,\rm\frac{Ct}{s}[/math]
Das Haus soll statt mit der Ölheizung mit einer Wärmepumpe geheizt werden. Die Wärmepumpe nimmt die Entropie aus einem vorbeifließendem Bach.
Die Temperatur des Wassers im Bach ist 10°C, die des Hauses 25°C. Das Haus verliert ständig Entropie an die Umgebung, und zwar pro Sekunde 30 Carnot. Damit es seine Temperatur behält, muss die Wärmepumpe diese Entropie ständig nachliefern.
Wie hoch ist der Energieverbrauch der Wärmepumpe?
Berechnung:
Da die Wärmepumpe die Temperatur des Hauses nur von 10°C auf 25°C "anhebt", muss man als Potentialdifferenz der Entropie die Temperaturdifferenz, d.h. 15K , betrachten:
- [math]25^\circ \,\rm C - 10^\circ \,\rm C = 15\,\rm K[/math]
- [math]I_E=I_S \, T = 30 \,\rm \frac{Ct}{s} \cdot 15 \,\rm K = 450 \,\rm W[/math]
Das ist nur ein Bruchteil des Energiebedarfs der Ölheizung! Allerdings ist dies nur eine sehr optimistische Überschlagsrechnung. Gerade im Winter dürfte der Bach eine niedrigere Temperatur haben und außerdem treten Energieverluste an der Wärmepumpe auf. Der entscheidende Faktor, der hier unberücksichtigt bleibt, ist aber die Energiequelle der Pumpe. Bezieht diese ihre Energie aus dem Strom eines Kohlekraftwerkes mit einem Wirkungsgrad von 1/3, so muss man den eigentlichen Energiebedarf der Pumpe verdreifachen.
Kochplatte
Träger: Entropie S
Potential: Temperatur [math]T[/math]
- [math]I_E=I_S\,T \quad \text{}[/math] oder [math]\text{}\quad \dot E=\dot S \,T[/math]
Um die in einem "warmen" Gegenstand enthaltene Energiemenge zu bestimmen, könnte man sich vorstellen, dass man ihn vom absoluten Temperaturnullpunkt an erwärmt. Während des Erwärmens fließt ständig Entropie und damit auch Energie hinein. Da die Temperatur sich dabei verändert, müßte man einen genauen Entropieverlauf in Abhängigkeit der Temperatur kennen.
Einfacher ist der Fall, dass sich die Temperaturen von Herdplatte und Topf nach einer längeren Zeit auf konstante Temperatur [math]T_1[/math] und [math]T_2[/math] eingependelt haben. Für diesen Fall gilt wieder, dass pro Sekunde die Energiemenge [math]E= S \, T [/math] in den Topf fließt.
Da jedoch die Temperaturen von Kochplatte und dem Topf (bzw. dem Wasser) unterschiedlich sind, stoßen wir auf eine Besonderheit: Da vorausgesetzt ist, dass der Energiestrom konstant ist, d.h. dass keine Energieverluste auftreten, das System jedoch eine Temperaturdifferenz aufweist, muss, um der Forderung gerecht zu werden, Entropie erzeugt werden. D.h. durch das Fließen der Entropie wird "neue" Entropie erzeugt. Dies ist vergleichbar mit einem elektrischen ohmschen Widerstand. Dort fließt elektrische Ladung durch das Kabel und dabei wird Entropie erzeugt, also das Kabel erwärmt.
Temperatur der Kochplatte: [math]T_1[/math] Temperatur des Topfes: [math]T_2[/math]
Mit [math]I_E=I_S \,T[/math] folgt für den Entropiestrom aus der Platte: [math]{I_S}_1= \frac{I_E}{T_1} [/math]
für den Entropiestrom in den Topf: [math]{I_S}_2=\frac{I_E}{T_2} [/math], woran man erkennt, dass [math]{I_S}_1 \lt {I_S}_2[/math]!
Oder, anders gesagt, es fließt pro Sekunde die Energie [math]E= S_1 \, T_1 [/math] aus der Kochplatte raus und die Energie [math]E= S_2 \, T_2 [/math] in den Topf rein. Weil die Temperatur aber dabei abnimmt, und die Energie dabei erhalten bleibt, muss die Entropiemenge zugenommen haben.
Berechnung von Energiemengen bei veränderlichem Potential
Allgemein
Das Potential [math]\varphi[/math] ist das Energiebeladungsmaß, es gibt an, wieviel Energie mit dem Energieträger transportiert wird. Wenn das Potential während eines Vorgangs sich verändert, so transportiert die gleiche Menge des Trägers mal mehr und mal weniger Energie. Das muss man berücksichtigen.
Man erreicht dies, indem man den gesamten Vorgang gedanklich in viele "kleine" Zeitspannen zerlegt, in denen das Potential annähernd konstant bleibt. Dann summiert man über alle "kleinen" Zeitspannen.
Die Änderungsrate der Energie [math]\dot E[/math] oder Leistung [math]P[/math], ist proportional zur Änderungsrate des Trägers [math]\dot Tr[/math]:
- [math]\dot E = P = \varphi \, \dot Tr[/math]
Für eine "kurze" Zeitspanne [math]\Delta t[/math] kann man das näherungsweise als Differenzenquotient schreiben:
- [math]\frac{\Delta E}{\Delta t} = \varphi \, \frac{\Delta Tr}{\Delta t} \quad \Rightarrow \quad \Delta E = \varphi \, \Delta Tr[/math]
Will man nun die insgesamt geflossene Energiemenge berechnen, so summiert man alle kleinen Energiemengen. Mit anderen Worten, man integriert über die Trägermenge:
- [math]E \approx \sum_i \Delta E_i = \sum_i \varphi \, \Delta Tr_i \quad \Rightarrow \quad E =\int \varphi(Tr) \, dTr[/math]
|
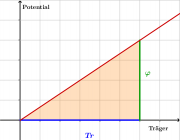
Trägt man das Potential über der Trägermenge auf, so entspricht die Fläche unterhalb des Schaubildes[3] der Gesamtänderung der Energie:
Die Fläche kann man auch mit dem Mittelwert [math]\bar \varphi[/math] der Potentialfunktion [math]\varphi (Tr)[/math] berechnen:
|
Stausee
Träger: m (Schwerefeld)
Potential: gh
- [math]I_E=I_m\, gh \qquad[/math] oder: [math]\dot E= \dot m\, gh[/math]
Zur Berechnung der Gesamtenergie des Sees stellt man sich vor, dass man den leeren See auffüllt. Die Höhe "0m" soll am Boden des Sees sein.
Fließt das Wasser auf einer konstanten Höhe in den See, so fügt jede Masse m dem See die Energie [math]E=m\,gh[/math] zu.
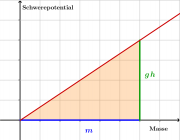
Weil aber während des Füllens die Höhe und somit das Potential ansteigt, muss man wieder die Fläche im gh(m)-Diagramm bestimmen (integrieren) oder die mittlere Höhe benutzen:
- [math]E = \int gh(m) \, dm = m\, g \, \bar h[/math]
Über die mittlere Höhe kann man auch den Schwerpunkt festlegen:
- [math]E=m \, g h_S[/math]
Bei einem Wasserbecken oder einem Wasserglas mit konstantem Querschnitt ist die mittlere Höhe die halbe Höhe, es gilt dann:
- [math]E=\frac{1}{2}m\,gh[/math]
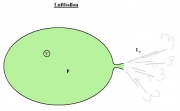
aufgeblasener Luftballon
Trägergröße: Volumen
Potential: Druck
- [math]I_E=I_v \, p \qquad[/math] oder: [math]\dot E= \dot V \,p[/math]
Wenn beim Druck [math]p[/math] der Luftballon um das Volumen [math]V[/math] kleiner wird, so verringert sich die enthaltene Energie um [math]\Delta E = \Delta V \, p[/math].[4]
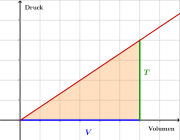
Durch das Herauslassen der Luft wird sich aber der Druck im Ballon ändern, weshalb man zur Bestimmung der gesamten Energiemenge die Fläche im p(V)-Diagramm bestimmen oder den mittleren Druck [math]\bar p[/math] verwenden muss. Die Fläche kann man als Integral schreiben. (Info zum p(V)-Diagramm)
- [math]E = \int p(V)\, dV = V \, \bar p[/math]
Wenn der Druck sich gleichmäßig ändert, dann ist der mittlere Druck gerade der halbe Maximaldruck:
- [math]E= \frac{1}{2}\, V \, p[/math]
- Beispiel
Der aufgeblasene Ballon hat ein Volumen von [math]V=3\,\rm l[/math]
Der Innendruck liegt [math]p=45\,\rm mbar[/math] über dem Normaldruck.
Vereinfachend nimmt man an, dass beim Herauslassen der Luft der Druck im Ballon linear abnimmt. Für die dabei freiwerdende Energie gilt:
- [math] \begin{array}{rcl} E &=& \frac{1}{2}\, V \, p \\ &=& \frac{1}{2} 3\,\rm l \cdot 45\,\rm mbar\\ &=& \frac{1}{2} 3\,\rm l \cdot 45\,\rm hPa\\ &=& \frac{1}{2}\,3\!\cdot\!10^{-3}\,\rm m^3 \cdot 45\!\cdot\!10^2\,\rm Pa\\ &=& 13{,}5 \,\rm J \end{array} [/math]
geladener Kondensator
Träger: elektrische Ladung
Potential: elektrisches Potential
- [math]I_E=I_v \, p \qquad[/math] oder: [math]\dot E= \dot V \,p[/math]
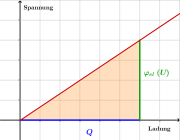
Zur Energiebestimmung verfolgt man den Ladevorgang, bei auf dem Kondensator die Ladung [math]Q[/math] von einer Platte auf die andere verschoben wird.
Jede kleine Ladungsmenge [math]\Delta Q[/math] muss die Potentialdifferenz (Spannung) [math]\Delta \varphi = U[/math] "hinaufgehoben" werden, wozu die Energie [math]\Delta E = U \, \Delta Q [/math] nötig ist. Die Spannung bei einem idealen Kondensator ist proportional zur verschoben Ladung, daher gilt für die Fläche unter dem U(Q)-Diagramm:
- [math]E= \frac{1}{2} \, Q \, U[/math]
rollender Wagen
Träger: Impuls [math]p[/math]
Potential: Geschwindigkeit [math]v[/math]
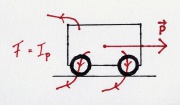
- [math]I_E=I_p\, v \qquad[/math] oder: [math]\dot E= \dot p\, v = F\, v[/math]
Um die Energiemenge des Wagens zu bestimmen beschleunigt man ihn aus dem Stand. Dabei wirkt eine beschleunigende Kraft und der Impuls fließt rein (nimmt zu).
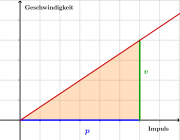
In diesem Fall ändert sich die Geschwindigkeit, also das Potential, während des Vorgangs. Es ist nicht korrekt zu sagen, dass der Wagen die Energiemenge [math]E=p\,v[/math] enthält. Wieder muss man die Fläche im p-v-Diagramm, also ein Integral, bestimmen oder die mittlere Geschwindigkeit verwenden:
- [math]E = \int v(p) \, dp = p\, \bar v[/math]
Nimmt man den einfachen Fall an, dass eine konstante Kraft wirkt, so nimmt die Geschwindigkeit gleichmäßig zu und die mittlere Geschwindigkeit ist daher die Hälfte der maximalen. Weil es aber egal ist, wie der Wagen auf diese Geschwindigkeit gebracht wurde, gilt diese Formel auch für alle anderen Beschleunigungsvorgänge! Demnach beträgt die Energie eines Gegenstandes mit dem Impuls p und der Geschwindigkeit v:
- [math]E=\frac{1}{2}p\,v = \frac{p^2}{2\, m} =\frac{1}{2}m\, v^2[/math]
Für diesen besonderen Fall kann man die Energie auch anders berechnen. Dazu betrachtet man wieder einen "kleinen" Teil der Bewegung, bei dem die Geschwindigkeit nahezu konstant ist:
Die Energie berechnet sich dann zu:
- [math]\Delta E = v \, \Delta p[/math]
Die Geschwindigkeit ist Strecke pro Zeit:
- [math]v =\frac{\Delta s}{\Delta t}[/math] , was man einsetzen kann:
- [math]\Delta E = \frac{\Delta s}{\Delta t} \, \Delta p = \frac{\Delta p}{\Delta t} \, \Delta s = F \, \Delta s[/math]
Man erhält die "Goldene Regel der Mechanik": Die Energie berechnet sich als "Kraft mal Weg", falls die Kraft längs des Weges konstant ist. Andernfalls berechnet man die Fläche im F(s)-Diagramm.
- Beispiel
Ein Auto mit 1t Masse fährt mit 72km/h.
Die Größen rechnet man zunächst in Standardeinheiten um, dann kann man die Impulsmenge bestimmen:
- [math]m=1000\,\rm kg[/math] und [math]v=20\,\rm\frac{m}{s}[/math]
- [math]p=m\, v = 1000\,\rm kg \cdot 20\,\rm\frac{m}{s} = 20000\,\rm Hy[/math]
Damit berechnet sich die Energie zu:
- [math]E=\frac{1}{2}p\,v =\frac{1}{2}20000\,\rm Hy \cdot \, 20\,\rm\frac{m}{s} = 400000\,\rm J =0{,}4\,\rm MJ[/math]
Kennt man den Kraftverlauf mit dem das Auto beschleunigt wurde und den Weg längs dem beschleunigt wurde, so kann man die Energie auch mit der Goldenen Regel berechnen:
Wenn der Wagen von der konstanten Kraft (ziemlich unrealistisch!) der Stärke 800N längs der Strecke von 500m beschleunigt wird, erhält man:
- [math]E= 800\,\rm N \cdot 500\,\rm m = 400000\,\rm J[/math].
Literatur
- Das Energiebuch ; Prof. Dr. Gottfried Falk, Prof. Dr. Friedrich Herrmann et al, Schroedel Verlag, Hannover, 1981
Links
- Vortrag: Energiespeicherung (Uni Tübingen)
- Artikel über Energiespeicher (Ivan-Israel Garay, Tim Termeer, Seminar von Gregor Krause, FH Aachen)
- Entropieerklärung (Gymnasium Ried)
- E-Learning ZHAW Kurs: Thermodynamik (maur) Buch: Theorie Wärme
Geschichte des Energiebegriffs
- des Begriffs Wikipedia: Geschichte des Energiebegriffs
- LEIFI: Geschichte des Energiebegriffs
- Die Entdeckung der Energie von Udo Leuschner, inhaltlich teilweise diskutabel, vor allem der Teil über Wärme als Stoff, aber einige interessante Stichpunkte
Fußnoten
- ↑ Der Karlsruher Physikkurs verwendet das Wort "Wärme" entgegen des heute üblichen Gebrauchs, im Sinne der Entropie. Der Begriff "Wärme" ist umgangssprachlich mit beiden physikalischen Größen verwandt. Hilfreich ist daher das Wort "Wärme" entweder zu vermeiden oder immer noch zu ergänzen und z.B. von der "Wärmeenergie" oder auch der "Wärmeentropie" zu sprechen. Ähnlich verhält es sich bei den umgangssprachlichen Begriffen "Schwung" und "Wucht", die sowohl dem Impuls als auch der Energie einer Bewegung zugeordnet werden können.
- ↑ Wird z.B. Luft in einer Luftpumpe schnell komprimiert, so wird wenig bis keine Entropie an die Umgebung abgegeben. Die Entropiemenge der Luft bleibt daher konstant und die Luftmenge ist der einzige Energieträger, der sich ändert. (Video von Tilo Hemmert, Universität Würzburg) Auch bei wenig kompressiblen Stoffen, wie Wasser und anderen Flüssigkeiten, spielt die Entropieänderung keine Rolle.
- ↑ Mit Hilfe eines grafikfähigen Taschenrechners oder entsprechender Software kann man Flächen unter Schaubildern numerisch bestimmen. Für den TI-83 gibt man zunächst die Funktion f(x)im Funktionenfenster (Y=) ein. Danach muss man die Fenstergröße so einstellen, dass der gewünschte Bereich sichtbar ist (WINDOW oder ZOOM). Dann kann man das Integral berechnen. Man wählt den Befehl CALC -> 7:Sf(x)dx und gibt die Grenzen lower und upper limit an, am einfachsten, indem man sie eintippt.
- ↑ Dabei wird vorausgesetzt, das der Vorgang schnell genug geschieht, sodass die Luft "keine Zeit hat" Entropie mit der Umgebung auszutauschen. Dies ist auch eine realistische Annahme, weil Luft ein schlechter Wärmeleiter ist. Somit ist der Luftstrom aus dem Ballon die einzige Veränderung eines Energieträgers. Läßt man dagegen die Luft ganz langsam aus dem Ballon, so wird sich die Temperatur der Luft im Ballon an die Außentemperatur angleichen, wodurch sich sich die Entropiemenge der Luft im Ballon ändert. In diesem Fall würden sich zwei Energieträgermengen gleichzeitig verändern.