Aufgaben zur Dynamik (Lösungen)

Jemanden anschieben

Eine Person wird auf einem Bürodrehstuhl angeschoben. Ihre (träge) Masse beträgt 70kg und die des Stuhls 10kg. Dabei wird sie 2m/sec schnell.

• Die Impulsmengen betragen:

Person: [math]p= m\, v = 70\, \rm kg \cdot 2\, \rm m/s = 140\, \rm Hy[/math]

Stuhl: [math]p= m\, v = 10\, \rm kg \cdot 2\, \rm m/s = 20\, \rm Hy[/math]

Zusammen also [math]160 \,\rm Hy[/math]

• Weil hier der Stuhl vor der Beschleunigung in Ruhe war, also noch keinen Impuls hatte, ist die Impulsänderung genau die Impulsmenge nach dem Anschubsen. Nach dem Veränderungsgesetz ändert sich der Impuls um:

[math]\triangle \, p = F\, \triangle \, t[/math]

[math] 160 \, \rm{Hy} = F\, \cdot 1\, \rm{s} \quad \Rightarrow \quad F= 160 \, \rm N [/math]

Bei einer Sekunde hat man also mit 160N geschoben, bei der halben Zeitspanne muss die mittlere Kraft doppelt so groß gewesen sein.

Losfahren

Eine RadlerIn beschleunigt aus dem Stand 10 Sekunden lang mit einer mittleren Kraft von 30 Newton. Zusammen mit dem Rad hat sie eine (träge) Masse von 60kg.

• Weil hier das Rad vor der Beschleunigung in Ruhe war, ist die Impulsänderung genau die Impulsmenge nach den ersten zehn Sekunden. Nach dem Veränderungsgesetz ändert sich der Impuls um:

[math]\triangle \, p = F\, \triangle \, t = 30\, \rm N \cdot 10\, s = 300\, Hy[/math]

Aus der Definition des Impulses folgt:

[math]p= m\, v[/math]

[math]300 \, \rm{Hy} = 60\, \rm{kg} \cdot v \quad \Rightarrow \quad v = 5\, m/s = 18\, km/h[/math]

Die Weltraumwaage SLAMMD

Das "Space Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. (Demovideo)

Bei einer Messung wurde die Person durch eine Kraft von 50 Newton in 1,2 Sekunden auf eine Geschwindigkeit von 0,8 Meter pro Sekunde beschleunigt.

• Man kann den Impuls der Astronautin auf zwei Arten bestimmen. Einmal über das Veränderungsgesetz als Ergebnis der Kraftwirkung und einmal über die Definition des Impulses als Masse mal Geschwindigkeit. Auch hier ist die Impulsänderung genau die Impulsmenge nach der Beschleunigung, weil die Astronautin zu Beginn noch keinen Impuls hat:

[math] m\, v = \triangle \, p = F\, \triangle \, t[/math]

Nach der Masse aufgelöst:

[math]m= \frac{F\, \triangle \, t}{v} = \rm \frac{50\, \rm N \cdot \, 1{,}2\, s}{0{,}8\, m/s} = \frac{60\, \rm Hy}{0{,}8\, m/s} = 75\,kg[/math]

Die Masse beträgt 75kg.

Wasserwerfer

Der Wasserstrahl eines Wasserwerfers hat soviel Impuls, dass er Menschen umwerfen kann. Hält man in einem vereinfachten Experiment ein Brett in den Wasserstrahls eines Gartenschlauchs, so spürt man eine Kraft. Mit dieser Kraft wird das Wasser bis zum Stillstand abgebremst!

Aus einem Schlauch spritzen pro Minute 6 Liter Wasser. Man misst eine Kraft von 0,5 Newton auf das Brett.

• In der Zeit von 60s werden 6kg Wasser abgebremst. Wiederum ist die Impulsänderung der gesamte Impuls, weil das Wasser bis zur Ruhe abgebremst wird:

[math] m\, v = \triangle \, p = F\, \triangle \, t[/math]

Diesmal sucht man die Geschwindigkeit, die anderen Größen sind bekannt:

[math]v = \frac{F\, \triangle \, t}{m} = \rm \frac{0{,}5\, \rm N \cdot 60\, s}{6\, kg} = \frac{30 \,Hy}{6\, kg} = 5\,m/s[/math]

Das Wasser hat eine Geschwindigkeit von 5m/s (18km/h).

Pelton-Turbine

Hält man statt des Bretts eine Schale in den Wasserstrahl, die den Strahl um 180° umlenkt, kann man eine (fast) doppelt so große Kraft messen. (Dieser Effekt wird bei der sogenannten Pelton-Wasserturbine ausgenutzt. Verschiedene Videos dazu: Pelton Turbine/Wheel Working & Design, WATER TURBINE PELTON COSTA RICA 1, Pelton-Turbine (Aufbau und Funktionsweise) 3D-Animation)

• Warum ist die Kraft (fast) doppelt so groß?

Turmspringen

Eine Turmspringerin läßt sich vom 10-Meter-Turm fallen. Sie hat eine Masse von 60 kg.

• Mit welcher Kraft wird sie beschleunigt?
• Wie groß ist ihr Impuls und ihre Geschwindigkeit nach 1, 2, 3 Sekunden? (nach x Sekunden?)
• Vergleiche mit dem Fall ihres um 20kg "schwereren" Vereinskameraden.
  • die Impuls- und Geschwindigkeitszunahme,
  • den Aufprall auf der Wasseroberfläche.

Am Wasserhahn

Bestimme die Austrittsgeschwindigkeit des Wassers am Hahn.

Man hat folgende Hilfsmittel zur Verfügung: eine Waage (mit einer Plastiktüte zum Schutz), ein Messbecher und eine (Stopp-)Uhr.

Beschreibe den Aufbau, die Messergebnisse und die Auswertung.

Messung

Anzeige der Waage: 95 g

Innerhalb von 5 Sekunden fließen 870 ml Wasser aus dem Hahn.

Auswertung

Innerhalb der Zeit [math]t = 5sec[/math] wird das Wasser an der Waage bis zur Ruhe abgebremst. Dabei verliert es seinen gesamten Impuls von [math]p = m \, v[/math] durch die bremsende Kraft [math]F = 0,95 N[/math].

Wegen [math]p = m \, v = F \, t \qquad.[/math] folgt: [math]v= \frac{F \, t}{m}[/math] mit den gemessenen Werten:

[math]v= \frac{4,75 Hy}{0,87kg} \approx 5,46 \frac{m}{sec} \approx 19,7 \frac{km}{h}[/math]

Das Wasser ist also ungefähr 20 km/h schnell.

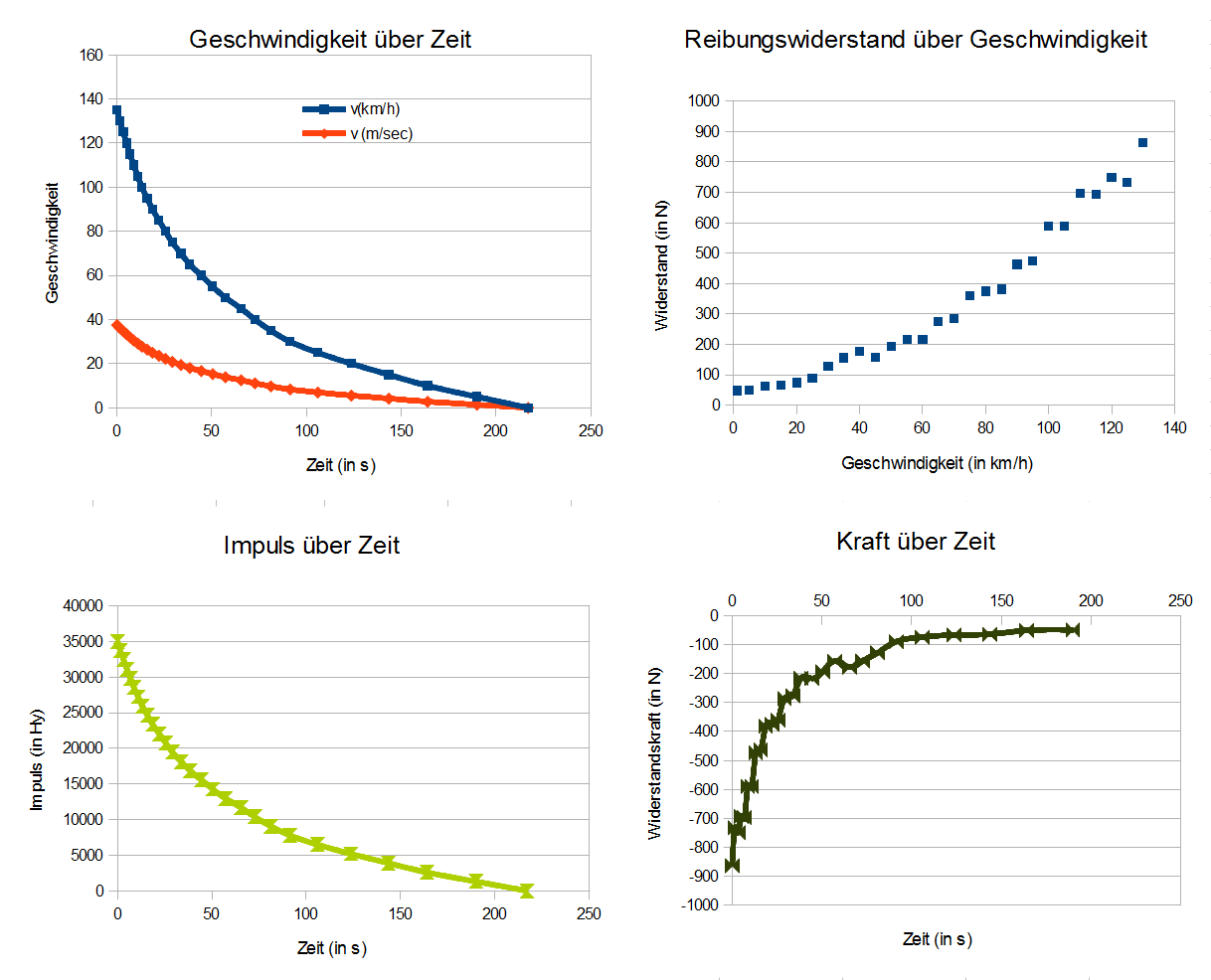
Luft- und Rollwiderstand eines Autos

Aus dem Geschwindigkeitsverlauf läßt sich auf den Verlauf des Impulses schließen. Der Impuls des Autos nimmt mit der Geschwindigkeit ab, genauer gilt:

[math]p=m \, v[/math]

Die wirkende Widerstandskraft sorgt dafür, dass der Impuls kleiner wird, genauer ist die Kraft gerade die zeitliche Änderungsrate des Impulses. Aus den gemessenen Werten kann man in einzelnen Zeitschritten jeweils die mittlere Änderungsrate am Diagramm als Steigung oder anhand der Wertetabelle als Differenzenquotient berechnen:

[math]F=\dot p \approx \frac{\triangle p}{\triangle t}=\frac{p(t_2)-p(t_1)}{t_2-t_1}[/math]

Alternativ dazu kann man auch zunächst die Beschleunigung des Autos als die zeitliche Änderungsrate der Geschwindigkeit bestimmen. Und dann daraus die wirkende Kraft:

[math]a=\dot v \approx \frac{\triangle v}{\triangle t} = \frac{v(t_2)-v(t_1)}{t_2-t_1}[/math]

[math]F=m \, a[/math]

Es ist zu erkennen, dass die Geschindigkeit und damit auch der Impuls zunächst stark mit der Zeit abnimmt. Rollt der Wagen schon länger, so nimmt der Impuls weniger schnell ab. Das heisst, die Widerstandskraft nimmt mit der Zeit ab.

Die Abnahme der Kraft kann nur mit der Abnahme der Geschwindigkeit zusammenhängen. Man sieht im Kraft-Geschwindigkeit-Diagramm deutlich, wie der Widerstand zunimmt. Bei der Verdoppelung der Geschwindigkeit von 50 km/h auf 100 km/h steigt der Widerstand ungefähr auf das Dreifache.

Auch bei einer sehr geringen Geschwindigkeit sinkt der Widerstand nicht unter 50 Newton. Dieser Anteil des Widerstandes scheint geschwindigkeitsunabhängig zu sein.

Ein Fahrrad rollt bergab

Ein Fahrrad steht auf einer abschüssigen Strasse und rollt nach dem Lösen der Bremsen hinab. Die Person hat zusammen mit dem Rad eine Masse von 90kg. Für den Beginn der Bewegung ist die Reibung noch zu vernachlässigen und für den Geschwindigkeitsverlauf gilt:

[math]v(t)= 0,8 \frac{m}{sec^2} \, t[/math]

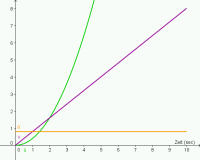
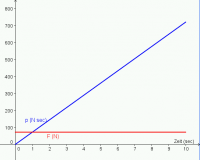
• Diagramme des zeitlichen Verlaufs der ersten 10 Sekunden:

• 

  Ort s (m), Geschwindigkeit v (m/sec) und Beschleunigung a (m/sec^2)

• 

  Impuls p (N sec) und Kraft F (N)

• Die Funktionsgleichungen lauten:

[math]s(t)=0,4 \frac{m}{sec^2}\,t^2[/math]

[math]v(t)=\dot s(t)= 0,8 \frac{m}{sec^2}\, t \qquad \qquad p(t)=m \, v(t) =72\frac{kg \, m}{sec^2}\,t = 72\frac{N \, sec}{sec}\,t =72 N\,t[/math]

[math]a(t)=\dot v(t)= 0,8 \frac{m}{sec^2} \qquad \qquad F(t)=\dot p(t) = m\, a(t) = 72 N[/math]

• Wieviel % Gefälle hat die Strasse?

Die Beschleunigung beträgt nur 0,8 m/sec^2 statt im freien Fall ca. 10 m/sec^2. Wegen des kleinen Winkels kann man daraus direkt ein Gefälle von 8% ablesen, mit folgender Begründung:

Das Gefälle der Straße ist der Tangens des Neigungswinkels:

[math] \tan(\alpha) = \rm{Gef \ddot a lle}[/math].

Vom Neigungswinkel hängt auch das Verhältnis von Hangabtriebskraft [math]F_\|[/math] und Gewichtskraft [math]F_G[/math], bzw. Hangabtriebsbeschleunigung [math]a_\|[/math] und Erdbeschleunigung [math]g[/math] ab:

[math]\sin(\alpha) = \frac{F_\|}{F_G} = \frac{m \, a_\|}{m \, g} = \frac{a_\|}{g} = \frac{0,8 \, m/{sec}^2}{10 \, m/ {sec}^2} = 0.08[/math]

Für kleine Winkel unterscheiden sich Sinus und Tangens nur geringfügig, deshalb beträgt das Gefälle 0,08 , also 8%.

Für eine genaue Rechnung bestimmt man zunächst den Neigungswinkel und daraus den Tangens:

Für die Hangabtriebskraft gilt:

[math]F=F_G \ sin( \alpha)[/math]

[math]72 N = 90 kg \, 9,81 \frac{N}{kg} \sin(\alpha)= 882,9 N \, \sin(\alpha)[/math]

Der Winkel der Straße beträgt demnach:

[math]\alpha = sin^{-1}(0,081549) \approx 4,678^\circ[/math]

Und daraus folgt für das Gefälle:

[math]tan(4,678^\circ)\approx 0,0818[/math]

Das Gefälle beträgt also 8,2%.