Bewegung im Raum - Vektorielle Geschwindigkeit

• 

  Wie schnell bewegen sich die Personen?
  (Video anschauen)

• 

  Ob dieses Flugzeug heil runter kommt?
  (Video anschauen])
  (Video: Landende B52)

• 

  Wie schnell ist das fahrende Schiff? (Applet)

• 

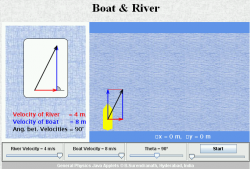
  Wie ein Boot über den Fluss fährt. (Applet)

Geschwindigkeit als vektorielle Größe

Beschreibt man die Geschwindigkeit eines bewegten Gegenstandes, so muss man angeben wie schnell er ist und in welche Richtung er sich bewegt.

Gibt es nur zwei mögliche Richtungen, wie Oben/Unten oder Links/Rechts, so kann man von positiven und negativen Geschwindigkeit sprechen. Kann die Bewegung in irgendeiner Richtung verlaufen, so beschreibt man die Geschwindigkeit mit einem Pfeil (oder auch "Vektor"). Der Pfeil zeigt in Richtung der Bewegung, seine Länge gibt den Betrag der Geschwindigkeit an.

Einen Vektor benennt man mit einem "gepfeilten" Buchstaben, ohne den Pfeil ist die Länge des Vektors gemeint:

• 

  Die Lokomotive kann nur vorwärts und rückwärts fahren.

• 

  Die Fußgänger können sich in der Ebene bewegen.

• 

  Das Flugzeug bewegt sich in drei Dimensionen.

Addition (Überlagerung) von Geschwindigkeiten

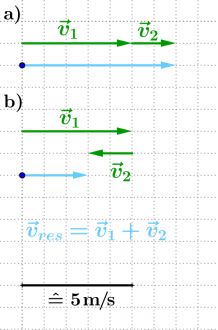
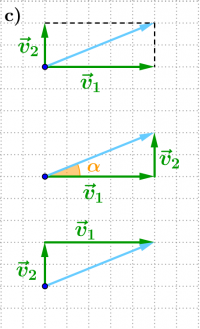
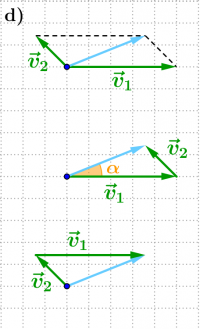
Geschwindigkeiten kann man mit einem Pfeildiagramm vektoriell addieren. Die resultierende Geschwindigkeit erhält man durch Aneinanderlegen der Pfeile oder durch ein "Vektorparallelogramm".

Bei (anti)parallelen Geschwindigkeiten könnte man statt mit Vektoren auch mit positiven und negativem Vorzeichen arbeiten.

• Ein Boot fährt auf einem Fluss
• 

  Der Fluss fließt mit der Geschwindigkeit [math]v_1 = 5\,\rm m/s [/math] nach rechts.
  Das Boot fährt mit [math]v_2 = 2\,\rm m/s [/math]
  a) nach rechts: [math]|\vec v_{res}| = v_{res} = 3\,\rm m/s[/math]
  b) nach links: [math]|\vec v_{res}| = v_{res} = 7\,\rm m/s[/math]

• 

  Der Fluss fließt mit der Geschwindigkeit [math]v_1 = 5\,\rm m/s [/math] nach rechts:
  c) Das Boot fährt mit [math]v_2 = 2\,\rm m/s [/math] rechtwinklig zur Flussrichtung.
  [math]|\vec v_{res}| = v_{res} \approx 5{,}4\,\rm m/s[/math]
  [math]\alpha = 21{,}8^\circ[/math]

• 

  Der Fluss fließt mit der Geschwindigkeit [math]v_1 = 5\,\rm m/s [/math] nach rechts:
  d) Das Boot fährt mit [math]v_2 = 2\,\rm m/s [/math] im Winkel von 45° schräg nach links:
  [math]|\vec v_{res}| = v_{res} \approx 3{,}9\,\rm m/s[/math]
  [math]\alpha = 21{,}5^\circ[/math]

• • Dementsprechend kann man Geschwindigkeiten auch subtrahieren.

Zerlegung einer Geschwindigkeit in Komponenten

An dem blauen Punkt kann man die Geschwindigkeit des Flugzeugs verändern.

Es wird angezeigt, wie schnell es sich in West-Ost-Richtung (v_x) und in Nord-Süd-Richtung (v_y) bewegt.

• Die Geschwindigkeit kann man in Komponenten zerlegen: In x-, y- und z-Richtung.

Aufgaben

1) Eine Rolltreppe

Alexander fährt die Rolltreppe hoch, er steht auf einer Stufe, die sich mit 80cm/s schräg nach oben bewegt. Die Rolltreppe ist mit 35° zur Horizontalen geneigt und überwindet einen Höhenunterschied von 15m.

a) Wieviel Meter legt Alexander pro Sekunde in horizontaler und vertikaler Richtung zurück? (Zeichnerische und rechnerische Lösung.)

b) Wie lange dauert die Fahrt?

2) Über den Fluss

Ein Fluss fließt mit einer Strömungsgeschwindigkeit von 1 m/s und ist 20m breit. Eva paddelt mit ihrem Schlauchboot über den Fluss und zwar genau senkrecht zum Ufer. Dabei ist sie relativ zum Wasser mit einer Geschwindigkeit von 1,5 m/s unterwegs.

a) Welche Geschwindigkeit hat sie relativ zum Ufer?

b) Wie lange dauert es, bis sie auf der anderen Seite ist?

c) Wieviel Meter wird sie vom Fluss abgetrieben?

Jetzt will Eva wieder zurückfahren, aber diesmal möchte sie nicht wieder abgetrieben werden, sondern genau auf der gegenüberliegenden Seite ankommen.

d) Welche Fahrtrichtung muss Eva wählen, wenn sie weiterhin mit 1,5 m/s paddelt?

e) Wie lange dauert die Fahrt?

3) Über den Atlantik fliegen

Ein Flug über den Atlantik zwischen Frankfurt und Los Angeles z.B. dauert ca. 11h 10min. Dabei legt das Flugzeug ca. 9.300km zurück.
Die Flüge dauern erstaunlicherweise in beiden Richtungen etwa gleichlang, obwohl in der Flughöhe von 10km Westwinde von bis zu 400km/h wehen, im Mittel kann man eine Windgeschwindigkeit von 100km/h annehmen.
Eine Boeing 747-8l hat eine maximale Reisegeschwindigkeit von Mach 0,86. Das sind 86% der Schallgeschwindigkeit und entspricht in 10km Höhe ungefähr einer Geschwindigkeit von 925km/h.

a) Wie lange braucht die Boeing für die Strecke Frankfurt-Los Angeles und zurück mindestens?

b) Angenommen es herrscht Windstille. Wie lange dauert der Flug nun hin und zurück mindestens? Vergleiche mit dem Hin- und Rückflug bei Westwind!

c) Wie schnell muss das Flugzeug mit und gegen den Wind fliegen, damit die angegebene Reisezeit von 11h 10min eingehalten werden kann?