Kinematik (Bahngeschwindigkeit und Frequenz) der Kreisbewegung

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche

Beispiele

  • Windräder sollen für Vögel gefährlich sein. Aber sie können doch den Rotorblättern einfach ausweichen, oder?

  • Was kann man hier mit dem Regler auf "16, 33, 45 oder 78" einstellen?

  • Was ist der Unterschied zwischen diesen drei Schallplatten? (Cd?)

  • Wie schnell bewege ich mich in Freiburg?

kinematische Beschreibung: Ort und Geschwindigkeit

Verschiedene "Drehgeschwindigkeiten": Wie schnell dreht sich das?


Stichworte:

Betrachtet man eine Drehbewegung, so gibt es zwei mögliche Antworten auf die Frage "Wie schnell ist es?".

Man kann beschreiben wie groß die "Drehgeschwindigkeit" ist:

  • als Umdrehungen pro Zeit. Die Schallplatte eines Plattenspielers dreht sich mit 33 oder 45 Umdrehungen pro Minute.
  • als Winkelgeschwindigkeit, also Winkel pro Zeit. Der Sekundenzeiger dreht sich mit einer Winkelgeschwindigkeit von 6° pro Sekunde.

Man kann beschreiben, wie groß die momentane Geschwindigkeit an einem bestimmten Ort ist:

  • die "Bahngeschwindigkeit"

[math]\omega=\frac{\alpha}{t}[/math]

Bild! / Animation

[math]b=\alpha r[/math] [math]v= \omega r[/math]

Animation der Kreisbewegung

Bewegungsgesetze der Kreisbewegung

Ein Gegenstand umläuft ein Drehzentrum im Abstand r und der Winkelgeschwindigkeit [math]\omega[/math]. Zu einem Zeitpunkt t möchte man wissen:

  • Wo ist der Gegenstand? (Ortsgesetz)
  • Wie schnell ist der Gegenstand? (Geschwindigkeitsgesetz)
  • Wie ändert sich die Geschwindigkeit? (Beschleunigungsgesetz)

Die Bewegung auf der Kreisbahn läuft in zwei Dimensionen ab, daher braucht man auch zwei Koordinaten, um den Ort zu beschreiben. Man legt den Ursprung des Koordinatensystems in das Drehzentrum. Zur Vereinfachung der Situation lassen wir die Zeit laufen, wenn der Gegenstand sich gerade durch den positiven Teil der x-Achse bewegt. Außerdem nehmen wir an, dass sich der Gegenstand gegen den Uhrzeigersinn bewegt. Diese Annahmen sind nicht notwendig, sie vereinfachen aber die folgende Rechnung.

Animation: Kreisbewegung im Koordinatensystem

Nach der Zeit t vergrößert sich der Winkel [math]\alpha[/math] um [math]\omega t[/math]. Der Ort des Gegenstands ist daher:

[math] [/math]
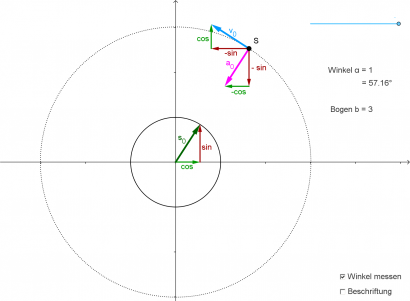
[math]\vec s(t)= r \begin{pmatrix} \cos(\omega\,t) \\ \sin(\omega\,t) \end{pmatrix}[/math]

Nun erhält man die Geschwindigkeit als zeitliche Änderungsrate des Ortes durch Ableiten nach der Zeit. Nach dem Unabhängigkeitsprinzip kann man dabei die x- und die y-Koordinate einzeln ableiten. Bei der Ableitung von [math]\sin(\omega\,t)[/math] muss man die Kettenregel beachten. Die innere Ableitung von [math]\omega\,t[/math] ist gerade [math]\omega[/math].

Durch eine weitere Ableitung nach der Zeit erhält man die Beschleunigung.

[math] \begin{array}{cc} \vec s(t)= \;\;\;\; r \begin{pmatrix} \;\;\cos(\omega\,t) \\ \;\;\sin(\omega\,t) \end{pmatrix} & \\ \vec v(t)= \;\omega\, r \begin{pmatrix} -\sin(\omega\,t) \\ \;\;\; \cos(\omega\,t) \end{pmatrix} \\ \vec a(t)= \omega^2\, r \begin{pmatrix} -\cos(\omega\,t) \\ -\sin(\omega\,t) \end{pmatrix} \end{array} [/math]


Interpretation
Die Einheitsvektoren des Ortes, der Geschwindigkeit und der Beschleunigung.

Alle Bewegungsgesetze sind der Form "Zahl mal Vektor". Die Vektoren haben alle die Länge eins und geben daher nur die Richtung an. Der Geschwindigkeitsvektor ist tangential zur Kreisbahn und die Beschleunigung zeigt zur Kreismitte. Die Zahl vor dem Vektor ist gerade der Betrag des Ortes, der Geschwindigkeit, usw.

Die Richtung der Vektoren verändert sich mit der Zeit, dagegen bleiben die Beträge immer konstant.

[math] \begin{array}{cc} \vec r(t)= \;\;\;\; r \ \vec {s_0} & \\ \vec v(t)= \;\omega\, r \ \vec {v_0} \\ \vec a(t)= \omega^2\, r \ \vec {a_0} \end{array} [/math]

Links

Von „http://schulphysikwiki.de/index.php?title=Kinematik_(Bahngeschwindigkeit_und_Frequenz)_der_Kreisbewegung&oldid=9596“