Aufgaben zum Licht als Welle (Lösungen)

Interferenz im Alltag

Die Interferenz, also die Überlagerung, von Licht tritt grundsätzlich immer auf. So kann Licht aus zwei Lampen zum Beispiel quer durch das Zimmer "fliegen" und sich durchkreuzen. Lichtschwerter gibt es nicht:).

Nur das typische Muster, die periodische Schwankung der Intensität, ist nicht immer zu beobachten. Solche Muster treten bei Wellen dann auf, wenn der Abstand der Lichtquellen oder die Breite eines Hindernisses im Bereich von einigen Wellenlänge des Lichtes liegt. (Vgl. Beugung an Öffnungen und Hindernissen) Im Alltag ist die Wellenlänge des Lichtes aber viel kleiner als die Breite der meisten Gegenstände.

Typische Welleneigenschaften

Typische Welleneigenschaften, die man auch von mechanischen Wellen kennt, sind:

1. Beugung
2. Brechung und Reflektion
3. Interferenz

Isaac Newton hat Licht als einen Strom von Teilchen beschrieben und konnte damit einfach die Reflektion wie das Abspringen von Bällen an einer Wand erklären. Auch die Brechung konnte er mit einer größeren Ausbreitungsgeschwindigkeit in einem Medium erklären. Die Beugung, also die Ablenkung, von Teilchen in der Nähe eines Hindernisses zu erklären hat auch Newton größere Probleme bereitet.

Vollkommen unvereinbar mit der Vorstellung von Lichtteilchen sind aber Interferenzerscheinungen. Vor allem das Zustandekommen eines Minimums ist nicht zu erklären. Denn wie sollen sich an einem Ort auftreffende Lichtteilchen gegenseitig auslöschen?

Beispiel-Experiment

Gegenstände oder speziell aufgebaute Experimente, bei denen man Interferenzmuster beobachten kann, sind ein guter Nachweis für den Wellencharakter von Licht:

Im Alltag: Schillernde CDs, Hologramme von Geldscheinen, [Seifenblasen, schillernde Federn von Vögeln, Perlmutt, ... (Siehe auch hier)

Im Experiment: Doppelspalt, Einzelspalt, Gitter, ...

Doppelspalt

Der Doppelspaltversuch ist auch mit mechanischen Wellen durchführbar und hier erklärt.

Der Versuch mit Licht ist hier beschrieben.

Haaresbreite

Näherungsweise kann man den Versuch als Doppelspaltexperiment auffassen, bei dem vom rechten und linken Rand des Haars jeweils eine Lichtwelle ausgeht.

Die betrachtete Stelle [math]P[/math] ist um [math]a[/math] aus der optischen Achse verschoben und [math]L[/math] vom Doppelspalt entfernt. Der Schirm befindet sich im Abstand [math]l[/math] vom Doppelspalt.
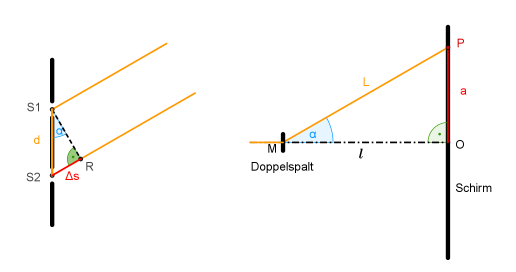
Die Spaltmitten haben einen Abstand [math]d[/math] voneinander und [math]\Delta s[/math] ist der Gangunterschied der beiden Strahlen.

[math]\sin(\alpha) = \frac{\triangle s}{d} = \frac{a}{L} =\frac{a}{\sqrt{a^2+l^2}}\approx \frac{a}{l} \qquad \triangle s: \text{Gangunterschied zu den ''Spaltmitten''}[/math]

[math]\triangle s = k \ \lambda \qquad \qquad \text{konstruktive Interferenz: Maximum k-ter Ordnung (k= 0,1,...)}[/math]

[math]\triangle s = k \ \lambda - 1/2 \ \lambda \quad \text{destruktive Interferenz: Minimum k-ter Ordnung (k= 1,2,...)}[/math]

Wir messen folgende Größen mit Mikrometerschraube und Lineal bei dem roten Laser:

Dicke des Haares: 0,05 mm
Abstand Haar-Wand: 1 m
Abstand Mitte des Musters - 2. dunkle Stelle: 1,8 cm

Man hat an der Stelle des 2. Minimums gemessen, der Gangunterschied beträgt daher [math]\Delta s = \frac{3}{2} \lambda[/math]:

[math]\frac{\frac{3}{2} \lambda}{d} \approx \frac{a}{l}[/math]

Das kann man nun nach der Wellenlänge auflösen:

[math]\lambda= \frac{2}{3} \frac{a}{l}\, d =\frac{2}{3} \frac{1{,}8\,\rm cm}{100\,\rm cm}\cdot 0{,}05\cdot 10^{-3}\,\rm m = 6\cdot 10^{-7}\,\rm m = 600\,\rm nm[/math]

Das ist nicht sonderlich genau, ergibt aber einen ungefähren Wert.

Lichtfarben und Wellenlänge

Ein Gitter wird vom Licht einer Glühlampe beleuchtet. Hinter dem Gitter ist im Abstand von 60cm ein Schirm. (Versuchsaufbau) Hier die Ergebnisse:

• 

  Gitter mit 80 Linien pro mm

• 

  Gitter mit 300 Linien pro mm

• Bestimmen Sie aus den Messergebnissen die Wellenlänge von violettem, blauen, grünem, gelben und rotem Licht. Vergleichen Sie Ihre Ergebnisse mit Literaturwerten.

a) Zur Berechnung der Wellenlängen kann man die gleiche Formel wie beim Doppelspalt heranziehen. Der Abstand der Spaltmitten d beim Doppelspalt entspricht hier ebenfalls dem Abstand der Spaltmitten, der sogenannten Gitterkonstante.

[math]\frac{\Delta s}{d} \approx \frac{a}{l}[/math]

Der Gangunterschied beträgt beim 1. Maximum gerade eine Wellenlänge, beim zweiten Maximum zwei Wellenlängen. Um die Wellenlänge zu berechnen muss man also nach dem Gangunterschied auflösen:

[math]\Delta s = \frac{a}{l}\, d[/math]

Gitter mit 80 Linien pro mm

[math] \begin{array}{rrcl} \textsf{1.Max:}& \Delta s &=& \lambda \\ \Rightarrow & \lambda &=& \frac{a_1}{l}\,d \\ & &=& \frac{a_1}{0{,6}\,\rm m}\cdot \frac{1}{80}\cdot 10^{-3}\,\rm m \\ & &=& \,a_1\cdot2{,}083\cdot 10^{-5}\,\rm m \\ \end{array} [/math]

[math] \begin{array}{rrcl} \textsf{2.Max:}& \Delta s &=& 2 \, \lambda \\ \Rightarrow & \lambda &=& \frac{1}{2}\,\frac{a_2}{l}\,d \\ & &=& \frac{1}{2}\, \frac{a_2}{0{,6}\,\rm m}\cdot \frac{1}{80}\cdot 10^{-3}\,\rm m \\ & &=& \,a_2\cdot 1{,}042\cdot 10^{-5}\,\rm m \\ \end{array} [/math]

	violett	blau	grün	gelb	rot
[math]\textsf{1.Max:}\ a_1\ \text{(in cm)}[/math]	[math]2{,}0[/math]	[math]2{,}2[/math]	[math]2{,}6[/math]	[math]2{,}8[/math]	[math]3{,}2[/math]
[math]\textsf{2.Max:}\ a_2\ \text{(in cm)}[/math]	[math]4{,}0[/math]	[math]4{,}5[/math]	[math]5{,}2[/math]	[math]5{,}6[/math]	[math]6{,}1[/math]
[math]\textsf{1.Max:}\ \lambda\ \text{(in nm)}[/math]	417	458	542	583	667
[math]\textsf{2.Max:}\ \lambda\ \text{(in nm)}[/math]	417	469	542	583	635

Obwohl man die Abweichungen vom 0. Maximum auf den Bildern nicht so genau abmessen kann, stimmen die gemessenen Werte stimmen sehr gut mit den Literaturwerten überein.

Gitter mit 300 Linien pro mm

Das Maximum erster Ordnung ist so breit, dass man für die einzelnen Farben ganze Wellenlängenbereiche angeben kann.

[math] \begin{array}{rrcl} & \Delta s &=& \lambda \\ \Rightarrow & \lambda &=& \frac{a_1}{l}\,d \\ & &=& \frac{a_1}{0{,6}\,\rm m}\cdot \frac{1}{300}\cdot 10^{-3}\,\rm m \\ & &=& \,a_1\cdot5{,}556\cdot 10^{-6}\,\rm m \\ \end{array} [/math]

	violett ab	blau ab	grün ab	gelb	rot ab	rot bis
[math] a_1\ \text{(in cm)}[/math]	[math]7{,}5[/math]	[math]8{,}5[/math]	[math]9{,}2[/math]	[math]10{,}6[/math]	[math]11{,}0[/math]	[math]12{,}5[/math]
[math]\lambda\ \text{(in nm)}[/math]	417	472	511	589	611	667

Vergleich man mit den Literaturwerten, so stellt man Abweichungen fest, die nicht nur an der Genauigkeit des Ablesens liegen können. Insbesondere stimmen die kürzeste und die längste Wellenlänge nicht mit den Literaturwerten überein. Zu Berücksichtigen ist, dass die Digitalkamera die gemessenen Farbwerte in nur drei Grundarben (rot, grün, blau) abspeichert und so den Originalfarbton nur nachahmen kann