Eingesperrte Quanten; der Potentialtopf

Zeigerdarstellung einer ebenen Welle

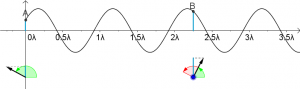
Bei den Anwendungen der Quantentheorie auf den Doppelspalt oder anderen Versuchen wurde bisher mit einer einfachen Wellen-Zustands-Funktion gerechnet, die nur durch ihre Wellenlänge und die Ausbreitungsgeschwindigkeit charakterisiert ist. Die Zustandsfunktion ist dabei im wesentlichen eine ebene Welle oder eine Kugelwelle, bei der man meistens auch noch die Abnahme der Amplitude vernachlässigt.

Ziel ist es nun, die Wellenfunktion eines Quantenobjekts zu finden, dass auf ein gewisses Raumgebiet beschränkt ist. Weiterhin befindet sich das Quant in einem Potential, es können also Kräfte wirken, die vom Ort abhängen.

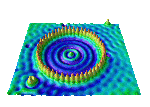
Hier sieht man, wie sich ein Elektron verhält, wenn es eingesperrt wird. Das Bild zeigt die Aufenthaltswahrscheinlichkeit eines Elektrons, das durch 48 Eisenatome eingesperrt wurde. Das Bild wurde mit einem Rastertunnelmikroskop aufgenommen. (IBM-Gallerie)

• 
• 
• 

Verschiedene Potentiale

Ein wichtiges, aber schon etwas schwierigeres Potential ist das Coulombpotential, das auch für die Beschreibung eines Atoms wichtig ist. Bei einem mehr oder weniger punktförmigen Objekt kennen wir das Verhalten sehr gut. Der Körper bewegt sich wie ein Satellit oder ein Planet im Gravitationsfeld.

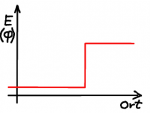
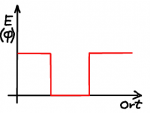
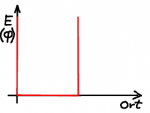
Einfacher sind Potentiale, deren Verlauf sprunghaft ist. Wie eine "Kante", bei der die potentielle Energie sprunghaft ansteigt oder eine Art von Mulde, in der das Potential kleiner ist. Die einfachste denkbare Realisierung eines "Quantenkäfigs" ist ein Potential, dass außerhalb eines Raumgebietes unendlich groß ist. Das Quant kann also diesen Potentialtopf nicht verlassen, es entspricht einem fest begrenzten Kasten.

• 

  Eine Kugel im Coulombpotential

• 

  Eine Kante im Potential

• 

  Ein Topf mit endlich hohen Wänden

• 

  Der unendlich hohe Potentialtopf

der Potentialtopf

Für den unendlich hohen Potentialtopf kann man heuristisch Lösungen finden ohne auf komplizierte Rechnungen zurückzugreifen. Von diesem sehr stark vereinfachten Modell kann man aber schon die prinzipielle Vorgehensweise lernen. Wellenfunktionen in den anderen Potentialen sind nur mit der Schrödingergleichung zu finden.

Herleitung der Energiewerte

Die Wellenfunktionen nehmen wir als stehende Welle an. Diese Annahme ist die einfachste, die man machen kann. Am Rand ist demnach die Aufenthaltswahrscheinlichkeit Null.

Nach de Broglie folgen damit aus den möglichen Wellenlängen [math]\frac{\lambda}{2}=\frac{a}{n}[/math] die jeweiligen Werte von Energie und Impuls. Bemerkenswert ist, dass diese Werte nur von der Breite des Topfes abhängen!

Bei einem Topf der Breite a kann ein Quant die Energiewerte [math]E= \frac{h^2}{8 m a^2} \quad n^2[/math] annehmen. Je kleiner des Topf, desto größer werden die Energiewerte und auch die Differenzen der Werte.

???

  * Einfaches Modell eines eingesperrten Quants (LaTex: e^-)
   * QT
   * LaTex: {E \over Q} 

Bild 5 vergrößern Bild 5

   * Idee: Stehende Welle als LaTex: \Psi
   * LaTex: |\Psi|^2 ist zeitlich konstant 

LaTex: \Rightarrow Keine Ladungsbewegung

LaTex: \Rightarrow Keine Strahlung

   * Wir rechnen nur mit den Zeigerlängen
   * Wellenlängen: LaTex: n*{{\lambda} \over 2} = a \Rightarrow {\lambda} = {2a \over n}
   * Energie/Impuls: LaTex: p = {h \over {\lambda}} = {h*n \over 2a} 

LaTex: E = E_Pot + E_Kin = 0 + {1 \over 2} *mv^2

Links

• Münchner Internetprojekt zur Lehrerfortbildung in Quantenmechanik
• Ein intuitiver Zugang zur Schrödingergleichung (Dr. Josef Küblbeck)
• Quantenphysik in der Schule mit Simulationen der Wellenfunktion in verschiedenen Potentialen