Aufgaben
Aus Schulphysikwiki
Version vom 6. Dezember 2016, 10:59 Uhr von Patrick.Nordmann (Diskussion | Beiträge)
Zeigermodell / Wellengleichung
- 1) Nachdem eine Schwingung innerhalb von 3 Sekunden 6 ganze Schwingungen ausgeführt hat, hat sich diese Störung um 1,8 m ausgebreitet.
- a) Bestimmen Sie Frequenz, Wellenlänge und Ausbreitungsgeschwindigkeit der Welle.
- b) Wie groß ist der Phasenunterschied zweier Schwingungen im Abstand von 3m und 33m?
- 2) Bei einer Pendelkette sind mehrere Pendel in einem Abstand von 10 cm miteinander gekoppelt.
- Wird ein Pendel angeregt, so folgen die Nachbarn 0,5 s später mit einer Phasenverschiebung von [math]\pi / 16[/math]. Bestimmen Sie die Ausbreitungsgeschwindigkeit, Wellenlänge und Frequenz der Welle.
- 3) Stellen Sie die Wellengleichung von Aufgabe 1) und 2) auf.
- 4) Eine Transversalwelle hat die Wellenfunktion [math]y(x,t)= 2\,{\rm cm} \, \sin(\frac{2}{\rm s} \cdot t -\frac{5}{\rm cm} \cdot x)[/math].
- a) Zeichnen Sie die Welle zum Zeitpunkt t=0, also zu Beginn der Zeitrechnung, und 0,32 Sekunden später in ein Koordinatensystem. (Mit dem GTR ist das ganz einfach!)
- b) Bestimmen Sie Amplitude, Frequenz und Wellenlänge.
- 5) Aus dem Baden-Württembergischen Physik-Abitur 2007: Aufgabe II a).
Interferenz
- 1) Woran kann man im Alltag erkennen, dass sich Wellen störungsfrei überlagern?
- 2) Beschreiben Sie den Versuch mit den zwei Lautsprechern, die an einem Sinusgenerator angeschlossen sind.
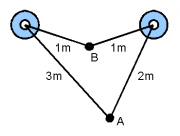
- 3) Die beiden Lautsprecher sind 1,5 m voneinander entfernt und schwingen in Phase mit einer Frequenz von 858 Hz.
- a) Bestimmen Sie die Lautstärke an den Punkten A und B mit Hilfe eines Zeigerdiagramms. Vernachlässigen Sie dabei die Abnahme der Schallintensität durch den größeren Abstand vom Lautsprecher und der Dämpfung.
- b) Suchen Sie zwei Stellen zwischen den Lautsprechern, bei denen der Ton besonders leise bzw. besonders laut ist.
- c) Wie verändert sich qualitativ die Situation in den Punkten A und B, wenn man die Änderung der Schallintensität nicht vernachlässigt?
- d) Bestimmen Sie die exakte Schwingungsgleichung für die Punkte A und B, wenn beide Lautsprecher mit einem Watt senden.