Dynamik (Zentripetalkraft und Bahnimpuls) der Kreisbewegung

(Klassische Mechanik > Kreisbewegungen)

Beispiele

• 

  Wie ist wohl dieses schöne Muster zustandegekommen?

• 

  Wie schafft es der Hammerwerfer diese Stahlkugel so weit zu werfen? Video: Weltrekordwurf von Youri Sedykh

• 

  Eine Technikstudie.

• 

  Wenn man einen Milchaufschäumer zum Reinigen...

• 

  in einen Wasserstrahl hält...

• 

  spritzt das Wasser nach allen Seiten weg.

• 

  Sitzt du lieber Außen oder Innen?

• 

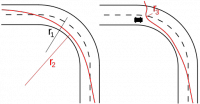
  Warum schneidet man beim Motorradrennen die Kurve?
  Video: Die Kurve schneiden

• 

  Wikipedia: Ideallinie

Versuch: Tennisball schleudern

Simuliert den Hammerwurf oder die Matsch-/Wasserspritzer.

• Wie fliegt der Ball weg?

Zu welchem Zeitpunkt muss man die Schnur loslassen um den Ball in eine bestimmte Richtung zu schleudern?

• Was verändert sich, wenn man schneller dreht?
• Was verändert sich, wenn man einen Ball mit mehr Masse schleudert?

Versuch: Karussell fahren

Aufbau

• 

  Ein kleines Karussell mit Playmobilfiguren.

Beobachtung

• 

  Bei langsamer...

• 

  und schneller Fahrt.

• Animation eines Karussells (Walter Fendt)

Versuch: Rutschende Münzen/fallende Männchen/rollende Kugeln

Münzen, Kugeln, Männchen drehen sich mit der gleichen Frequenz in unterschiedlichem Abstand zum Mittelpunkt auf einer drehenden Scheibe (Plattenspieler)

Wer fällt als erstes um?

qualitative Ergebnisse

• Eine Kraft hält den Gegenstand auf der Kreisbahn. Sie wirkt senkrecht zur Bahn in Richtung des Mittelpunkts der Kreisbewegung.

Ohne diese "Zentripetalkraft" fliegt der Gegenstand tangential auf einer geraden Linie weg!

• Hammerwerfen: Je größer die Masse des Gegenstandes und je größer die Frequenz, desto größer muß die Zentripetalkraft sein.
• Karussell fahren: Bei gleicher Frequenz braucht man weiter Außen die größere Zenripetalkraft!
• Kurve fahren: Bei gleicher (Bahn)Geschwindigkeit braucht man für eine engere Kurve die größere Zentripetalkraft!

• Durch die Zentripetalkraft wird der Gegenstand nicht schneller. Die Zentripetalkraft ändert ständig die Richtung des Impulses, aber nicht die Menge des Impulses! Auch die Energiemenge bleibt konstant.

Versuch: Messung der Zentripetalkraft

Versuchsaufbau zur Messung der Zentripetalkraft.

Aufbau

Ein kleiner Wagen ist auf einer Schiene befestigt. Die Schiene kann mit einem Motor unterschiedlich schnell gedreht werden.

Eine Schnur ist an einem Kraftsensor und über eine Umlenkrolle am Wagen befestigt. Dreht sich die Schiene, so zieht die Schnur am Wagen und hält ihn so auf einer Kreisbahn. Diese Zentripetalkraft wird mit einem Kraftsensor gemessen.

Die Zentripetalkraft wird dann in Abhängigkeit vom Radius, der Winkelgeschwindigkeit und der Masse des Wagens gemessen. Dazu verändert man jeweils eine Größe und läßt die anderen konstant. Insbesondere ist von Interesse, wie sich bei einer Verdopplung des Radiuses oder der Winkelgeschwindigkeit oder der Masse die notwendige Zentripetalkraft ändert.

Mit einer Handstoppuhr kann man die Umlaufdauer ermitteln, am besten indem man die Zeit für 10 Umläufe bestimmt.

Die Masse wird mit einer Waage bestimmt.

Messungen

Ergebnisse

Berechnung der Zentripetalkraft

Ein Gegenstand mit bekannter Masse [math]m[/math] und Geschwindigkeit [math]v[/math] umläuft ein Drehzentrum im Abstand [math]r[/math].

• Welche Zentripetalkraft benötigt man, um den Gegenstand auf der Kreisbahn zu halten?

ohne Differentialrechnung

Man stellt sich eine Kugel vor, die innerhalb eines ringförmigen Billiardtisches ohne Reibung mit einer betragsmäßig konstanten Geschwindigkeit rollt.

Jedesmal, wenn die Kugel an die Bande stößt, erhält sie eine Impulsmenge, um die Richtung der Bewegung zu verändern. Der Betrag [math]p[/math] des Impulses bleibt dabei unverändert.

Verläuft die Bahn der Kugel nahe der Bande, stößt sie sehr oft und die Bahn nähert sich einer Kreisbahn an.

Bei der Zeichnung kann man mit dem Schieberegler die Anzahl der Ecken verändern:

Man entnimmt der Zeichnung sofort, dass die Impulsänderung, also auch die Kraft, in Richtung des Mittelpunktes gerichtet ist.

Den Betrag der Impulsänderung [math]\Delta p[/math] bei einem Stoß an der Bande kann man für ein beliebiges n-Eck berechnen. Man stellt fest, dass die Dreiecke [math]\triangle \rm MAB[/math] und [math]\triangle \rm NCD[/math] beide gleichschenklig sind und den gleichen "Spitzenwinkel" haben. Deshalb stimmen sie in allen Winkeln überein und sind ähnlich. Daraus, oder aus den Strahlensätzen, folgen die Verhältnisse:

[math] \begin{alignat}{2} \frac{\Delta p}{\Delta s} &= \frac{p}{r} & \quad |\cdot \Delta s \\ \Rightarrow \quad \Delta p &= \frac{\Delta s \, p}{ r} \end{alignat} [/math]

Zur Berechnung der Kraft benötigt man noch die Zeit, in der diese Impulsänderung stattfindet. Die Zeit für die Bewegung längs einer Seite des n-Ecks soll [math]\Delta t[/math] heißen. Im Mittel beträgt daher die Impulsänderung pro Zeit:

[math]\bar F = \frac{\Delta p}{\Delta t} = \frac{\Delta s \, p}{\Delta t \, r} [/math]

Der Quotient von Strecke und Zeit ist aber gerade die Geschwindigkeit der Kugel:

[math]\bar F = \frac{v \, p}{r} [/math]

Zur Vereinfachung kann man nun entweder den Impuls als [math]p=m\,v[/math] einsetzen oder die Winkelgeschwindigkeit [math]\omega =\frac{v}{r}[/math]:

[math]\bar F = \frac{m\, v^2}{r} = \omega \, p[/math]

Für eine immer größere Anzahl von Ecken wird die Bewegung kreisförmig und die Richtungsänderung kontinuierlich. Die mittlere Änderung des Impulses pro Zeit geht in eine momentane Änderung des Impulses über.

Diesen Grenzwertprozess kann man sich ersparen, wenn man die Differentialrechnung, also Ableitungen, verwendet.

mit Differentialrechnung

Die Einheitsvektoren des Ortes, der Geschwindigkeit und der Beschleunigung.

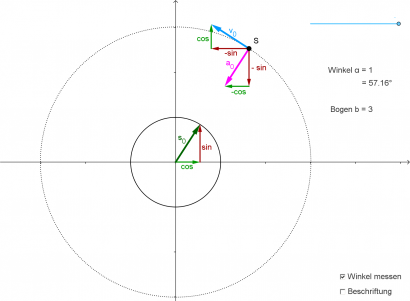
Die Bewegungsgleichungen der Kreisbewegung beschreiben den zeitlichen Verlauf des Ortes, der Geschwindigkeit und der Beschleunigung:

[math] \begin{array}{rrr} \vec s(t)= \;\;\;\; r \begin{pmatrix} \;\;\cos(\omega\,t) \\ \;\;\sin(\omega\,t) \end{pmatrix} = & \;\;\;\; r \ \vec {s_0} & \\ \vec v(t)= \;\omega\, r \begin{pmatrix} -\sin(\omega\,t) \\ \;\;\; \cos(\omega\,t) \end{pmatrix} = & \;\omega\, r \ \vec {v_0} \\ \vec a(t)= \omega^2\, r \begin{pmatrix} -\cos(\omega\,t) \\ -\sin(\omega\,t) \end{pmatrix} = & \omega^2\, r \ \vec {a_0} \end{array} [/math]

Der Impuls des Gegenstandes ist parallel zur Geschwindigkeit ([math]\vec p = m \, \vec v[/math]), man muss nur mit der Masse multiplizieren.

Die Kraft erhält man durch Ableiten des Impulses ([math] \vec F = \dot {\vec p}[/math]) oder als das m-fache der Beschleunigung ([math]\vec F = m \, \vec a[/math]):

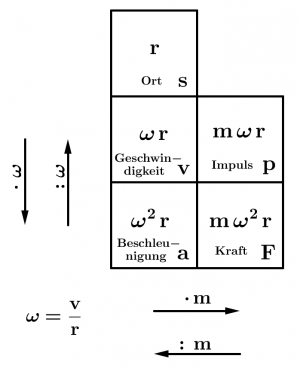
[math] \begin{array}{cc} \vec s(t)= \;\;\;\; r \ \vec {s_0} & \\ \vec v(t)= \;\omega\, r \ \vec {v_0} & \vec p(t)= m\,\omega\, r \ \vec {v_0} \\ \vec a(t)= \omega^2\, r \ \vec {a_0} & \vec F(t)= m\,\omega^2\, r \ \vec {a_0} \end{array} [/math]

Wie zu erwarten ist der Impulsvektor tangential zur Kreisbahn und die Kraft zeigt zur Kreismitte. Die Zahl vor dem Vektor ist der Betrag des Impulses und der Zentripetalkraft. Der Betrag des Impulses und der Kraft ändert sich nicht mit der Zeit, nur die Richtung von Impuls und Kraft ändern sich ständig.

Bewegt sich ein Gegenstand der Masse [math]m[/math] mit der Winkelgeschwindigkeit [math]\omega[/math] im Abstand [math]r[/math] um ein Drehzentrum, so hat er den Impuls [math] \vec p [/math] mit: [math] p = m\,\omega\, r [/math] Um den Gegenstand auf der Kreisbahn zu halten, benötigt man eine Zentripetalkraft [math]\vec F[/math] mit: [math] F = m\,\omega^2\, r [/math]

Formeln

Für gegebene Bahngeschwindigkeit

Beschreibt eine Situation, bei der die Bahngeschwindigkeit festgelegt ist. Z. B. ein Fahrrad (Auto, Inliner, ...), das in die Kurve fährt.

Man setzt dazu die Winkelgeschwindigkeit [math]\omega = \frac{v}{r}[/math] ein und kürzt mit dem Radius [math]r[/math]:

[math]F=\frac{m \, v^2}{r}[/math]

Die Zentripetalkraft ist bei fester Bahngeschwindigkeit antiproportional zum Radius! (doppelter Radius - halbe Kraft)

Für gegebene Winkelgeschwindigkeit

Beschreibt eine Situation, in der die Frequenz, Umlaufdauer oder Winkelgeschwindigkeit festgelegt ist. Z. B. eine Waschmaschine, Karussell, Plattenspieler, etc.

Die obige Berechnung der Impuls- und Kraftvektoren lieferte den Betrag der Zentripetalkraft. Mit [math]\omega = 2\,\pi\,f = \frac{2\,\pi}{T}[/math] läßt sich die Winkelgeschwindigkeit auch mit der Frequenz oder der Umlaufdauer berechnen.

[math]F = m \, \omega^2 r = m \ 4\, \pi^2 \! f^2 \; r = m \, \frac{ 4 \, \pi^2 }{T^2} \, r[/math]

Die Zentripetalkraft ist bei fester Frequenz proportional zum Radius! (doppelter Radius - doppelte Kraft)

Mischform mit Impuls

Mit [math]p = m \, v[/math] und [math]v=\omega \, r[/math] kann man die Größe der benötigten Zentripetalkraft auch mit dem Impuls ausdrücken:

Die Zentripetalkraft ist proportional zur Winkelgeschwindigkeit und zur Impulsmenge: [math]F = \omega\, p[/math] [math]\text{} \qquad \text{mit} \quad p=m\, v\qquad \text{und} \quad \omega = \frac{v}{r}[/math] "Man benötigt eine große Kraft um viel Impuls stark abzulenken."

Im Falle der konstanten Bahngeschwindigkeit ist auch der Impuls konstant. Die Winkelgeschwindigkeit und damit auch die Kraft ist antiproportional zum Radius. Denn bei doppeltem Radius ist die Winkelgeschwindigkeit nur noch halb so groß.

Im Falle der konstanten Winkelgeschwindigkeit steigt die Impulsmenge und damit auch die Kraft proportional zum Radius. Denn bei doppeltem Radius verdoppelt sich auch der Umfang und somit die Bahngeschwindigkeit und der Impuls.

Merkregel

Links

• youtube: hammer throw: 1986 Youri Sedykh's World Record Series
• Hammerwerferin Tatyana Lysenko
• Wikimedia Commons: Bilderserie zum Hammerwerfen

Zeugs

Handversuch: Gummiprofen an Schnur durch Rohr

Viele Möglichkeiten

Genaue Vorgaben machen

ZB Abhängigkeit Frequenz - Kraft

Radius - Kraft

Masse - Kraft