*

Mathematische Beschreibung des Doppelspalts (eine Formel:)

Man geht davon aus, dass von jeder Spaltmitte aus sich eine Elementarwelle ausbreitet. Damit erhält man genau die gleiche Situation wie bei der Zwei-Quellen-Interferenz von Schallwellen. Nun will man die Überlagerung berechnen, genauer, die Überlagerung an einer Stelle des Schirms.

Die betrachtete Stelle $$P$$ ist um $$a$$ aus der optischen Achse verschoben und $$L$$ vom Doppelspalt entfernt. Der Schirm befindet sich im Abstand $$l$$ vom Doppelspalt.
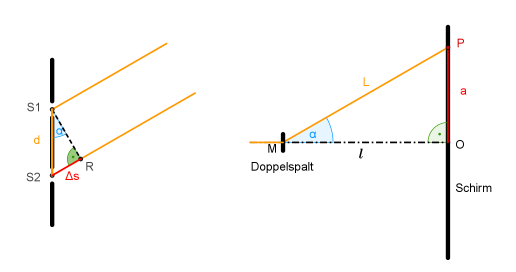
Die Spaltmitten haben einen Abstand $$d$$ voneinander und $$\Delta s$$ ist der Gangunterschied der beiden Strahlen.

An der Stelle $$P$$ überlagern sich zwei Schwingungen gleicher Frequenz, aber evt. unterschiedlicher Phase .

Die Phasenverschiebung hängt direkt mit dem Unterschied der Weglänge der Elementarwellen von den Spalten bis zur Stelle $$P$$ , dem sogenannten Gangunterschied $$\triangle s$$ zusammen. Ist z.B. $$\triangle s = 2 \ \lambda$$ , so ist die Phasenverschiebung $$2\cdot 2\pi$$ und die Amplitude der Schwingung ist groß ("konstruktive Interferenz"). Ist $$\triangle s = 1{,}5 \ \lambda$$ , so ist die Phasenverschiebung $$1{,5}\cdot 2\pi$$ und die Amplitude der Schwingung ist null("destruktive Interferenz").

In der weiteren Rechnung nimmt man vereinfachend an, dass die Strecken $$S_1 P$$ und $$S_2 P$$ parallel sind, was für einen "großen" Abstand zwischen Schirm und Spalt gerechtfertigt ist, denn dann ist $$L$$ wesentlich größer als $$d$$ . Diese Näherung wird auch "Fernfeld-Näherung", "Fraunhofer-Näherung" oder "Fraunhofer-Beugung" genannt. Dann sind die beiden rechtwinkligen Dreiecke $$S_1 R S_2$$ und $$M O P$$ ähnlich, denn sie haben gleiche Winkel. Demnach gilt:

$$\frac{\triangle s}{d} = \frac{a}{L} = \sin(\alpha)$$

Weil man den Abstand $$L$$ schlecht messen kann, $$l$$ aber gut, kann man $$L$$ entweder mit dem Satz des Pythagoras berechnen oder man setzt bei "kleinem" Winkel $$\alpha$$ auch einfach $$l \approx L$$ als Näherung ein:

$$\sin(\alpha) = \frac{\triangle s}{d} = \frac{a}{L} =\frac{a}{\sqrt{a^2+l^2}}\approx \frac{a}{l} \qquad \triangle s: \text{Gangunterschied zu den ''Spaltmitten''}$$ $$\triangle s = k \ \lambda \qquad \qquad \text{konstruktive Interferenz: Maximum k-ter Ordnung (k= 0,1,...)}$$ $$\triangle s = k \ \lambda - 1/2 \ \lambda \quad \text{destruktive Interferenz: Minimum k-ter Ordnung (k= 1,2,...)}$$