Aufgaben zum Konzept der Energie

(Kursstufe > Das Konzept der Energie)

Energiebedarf eines Menschen

Ein Mensch benötigt täglich etwa 10000 kJ Energie, die er durch das Essen erhält. (genauere Werte findet man zB. bei Wikipedia.)

• Berechnen Sie die mittlere Leistung in Watt.

Nudeln haben einen Brennwert von 1400 kJ/kg.

• Welche Menge an Nudeln müßte man pro Tag und wieviel pro Sekunde essen, wenn man damit ausschließlich seinen Energiebedarf deckt?

Ein Mühlrad

Auf ein Mühlrad fließen pro Stunde 18000 Liter Wasser. Das Mühlrad hat einen Durchmesser von 3m.

• Welche Leistung hat die Mühle maximal? (Gesucht ist also die Energiemenge pro Sekunde.)
• Vergleichen Sie das Mühlrad mit der Nahrungsaufnahme eines Menschen.

Ein Staubsauger

Auf einem Staubsauger steht:

Maximale Leistung: 1500W

• Wie groß ist die elektrische Stromstärke? (Gesucht ist also die Ladungsmenge, die in einer Sekunde durch den Sauger fließt.)
• Vergleichen Sie den Staubsauger mit dem Mühlrad.

Auto fahren

Läßt man ein Auto ohne Antrieb auf ebener Strecke rollen, so wird es immer langsamer. Die Geschwindigkeit und der Impuls nehmen mit der Zeit ab.

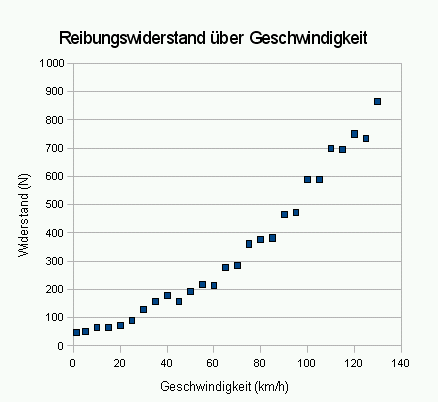
Darüber läßt sich der Widerstand des Autos bestimmen, der hier über der Geschwindigkeit aufgetragen ist. Man sieht deutlich, dass der Widerstand nicht linear mit der Geschwindigkeit ansteigt, was am Luftwiderstand liegt. Aus diesem Diagramm kann man einiges ablesen, bzw. berechnen.

• Welche Leistung benötigt man, um konstant 50km/h oder konstant 100km/h zu fahren?

Bei einem Ottomotor (Benziner) explodiert das Luft-Benzin-Gemisch bei einer Temperatur von 2000°C. Die Abgase haben eine Temperatur von lediglich 800°C.

• Warum kann deswegen der Wirkungsgrad dieses Motors nicht über 47% liegen?

Reale Ottomotoren haben einen Wirkungsgrad von ca. 25%.

• Welche Eingangsleistung braucht daher der Motor, um 50km/h oder 100km/h zu fahren? (Wieviel Benzin ist dazu nötig? Man kann den Energiegehalt eines Liters mit ca. 32MJ annehmen.

Energiebedarf einer Wärmepumpe

Eine Wärmepunpe funktioniert im wesentlichen wie ein Kühlschrank. Der Kühlschrank entzieht dem kalten Inneren Entropie und transportiert sie an das warme Abkühlgitter auf der Rückseite.

Ein Schwimmbad wird mit einer Wärmepumpe geheizt. Die Wärmepumpe nimmt die Entropie aus einem vorbeifließendem Bach und transportiert sie in das warme Wasser.

Die Temp. des Wassers im Bach ist 19°C, die des Wassers im Schwimmbad 23°C.

• Vergleiche die Wärmepumpe mit dem Mühlrad. Es gibt einen wesentlichen Unterschied!
• Wie kann man erklären, dass die Wärmepumpe Energie benötigt?

Das Wasser im Schwimmbad verliert ständig Entropie an die Umgebung, und zwar pro Sekunde 503Ct. Damit es seine Temp. behält, muss die Wärmepumpe diese Entropie ständig nachliefern.

• Wie hoch ist der Energiebedarf der Wärmepumpe?

Lageenergie eines Wasserturms

• Wieviel Lageenergie steckt wohl in dem Wasser des Turms? Genauer: Wieviel Energie könnte man erhalten, wenn man das Wasser am Fuße des Turmes herauslaufen läßt?

Der Wasserturm ist in etwa 20m breit und die maximale Wasserhöhe beträgt etwa 10m. Die tragende Betonsäule ist ca. 45m lang.

Erste Abschäzung

Schätzen Sie die mittlere Höhe des Wassers und berechnen so einen ersten Näherungswert.

Integrieren

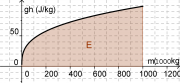
Man füllt den Turm mit einem konstanten Wasserstrom auf. Das Diagramm zeigt den Zusammenhang zwischen Wassermasse und Füllhöhe mal Ortsfaktor. Bestimmen Sie die Energiemenge durch eine ungefähre Flächenbestimmung. Jedes Rechteck entspricht [math]100000\,\rm kg \cdot 10\frac{\rm J}{\rm kg}=1\,\rm MJ[/math].

(Bemerkung für Neugierige: Die Funktion gh(V) ergibt sich aus dem Volumen eines Kegels: [math]V=\frac{1}{3}\, A\, h=\frac{1}{3}\, \pi r^2\, h[/math] und bei diesem Turm mit [math]h = r[/math]. Jetzt muss man noch nach h auflösen und mit g multiplizieren.)

Links

• Wikibooks: Vergleich Otto- und Dieselmotor
• LEIFI: Vergleich zwischen Otto- und Dieselmotor
• Energietechnik: Verbrennungsmotoren (Energie.ch, Rolf Gloor)