Das Induktionsgesetz und die magnetische Flussdichte
(Kursstufe > Elektro-Magnetismus)
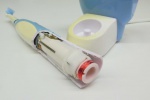
Elektrische Zahnbürste
Induktives Laden bei E-Autosein "Pickup" einer E-Gitarre (How Electric Guitar Pickups Work)
Der Tonabnehmer eines Schallplattenspielers (Wikipedia)
ein dynamisches Mikrophon (Wikipedia)
Inhaltsverzeichnis
- 1 Versuche: Induktion bei technischen Geräten
- 2 Versuche: Bewegte Leiter und Schleifen im Magnetfeld
- 3 Messen der Induktionsspannung bei Veränderung der Feldstärke (magnetische Feldkonstante)
- 4 Berechnung der Induktionsspannung mit der Lorentzkraft
- 5 Das Induktionsgesetz und der magnetische Fluss für Spezialfälle
- 6 Die magnetische Flussdichte
- 7 Das Induktionsgesetz und der magnetische Fluss im allgemeinen Fall
- 8 Versuch: Elektrisches Wirbelfeld
- 9 Fußnoten
- 10 Links
Versuche: Induktion bei technischen Geräten
- LED an Spule mit Eisenkern, Magnet an Eisenkern und wieder weg
- Oszi als Spannungsmessgerät
- eine Schleife um den Eisenkern, Magnet an den Kern
- Primärspule an Wechselspannung, Sekundärspule ans Oszi, mit/ohne Eisenkern
- Folgerung
Alle technischen Geräte nutzen die Änderung der magnetischen Polarisierung (Magnetisierung) eines Eisenkerns innerhalb einer Spule. Während der Änderung der magnetischen Polarisierung des Eisenkerns wird in der Spule eine Spannung induziert.
Der Tonabnehmer einer E-Gitarre
- Aufbau
Ein handelsüblicher Eisendraht wird zwischen zwei Befestigungen eingespannt. Verschiebt man die Tischklemmen, so kann man den Draht "stimmen".
Unter dem Draht befindet sich eine Spule (1000 Windungen) mit einem Eisenkern. Unterhalb des Eisenkerns klebt ein Festmagnet.
Die Spule ist über einen Vorverstärker und einem zweiten Verstärker, der als Endstufe dient, mit einem Lautsprecher verbunden.
Ein Oszilloskop zeichnet den Spannungsverlauf an der Spule direkt auf.
Dann kann man an der Drahtsaite an verschiedenen Stellen zupfen.
Hat man ein elektronisches Oszi zur Verfügung, so kann man sich auch das Frequenzspektrum anschauen.
Zur Demonstration des Funktionsprinzips kann man mit einem eisenhaltigen Gegenstand, wie einer Zange oder einem zweiten Eisenkern, über dem Tonabnehmer "herumwackeln".
- Beobachtung
Video des Demo-Versuchs mit einem zweiten Eisenkern.
Man hört den sonst recht leisen Ton der Saite über den Lautsprecher wesentlich lauter.
Zupft man mit dem Fingernagel, so hört sich der Ton schärfer an, und das Oszilloskop zeigt eine Schwingung mit vielen Oberfrequenzen.
Wenige Oberfrequenzen erreicht man mit dem Zupfen in der Mitte der Saite mit der weichen Seite des Fingers.
Versuche: Bewegte Leiter und Schleifen im Magnetfeld
Umkehrung des Leiterschaukel-Versuchs
Im Leiterschaukel-Versuch hat man durch ein Kabel oder eine Stange in einem Magnetfeld Strom fließen lassen. Dadurch wurde eine Kraft auf das Kabel ausgeübt und es hat sich bewegt.
Geht das auch andersherum? Eine Stange oder die Leiterschaukel wird im Magnetfeld bewegt und die Spannung an den Enden des Leiters gemessen. Dabei ändert man die Bewegungsrichtung und führt den Versuch auch mit vertauschten Polen aus.
- Beobachtung
Tatsächlich kann man eine geringe Spannung messen solange der Leiter sich bewegt. Sobald der Leiter still steht, misst man keine Spannung mehr.
Die Polung der Spannung hängt von der Bewegungsrichtung und von der Feldlinienrichtung ab.
- Folgerung
Immer, wenn ein Leiter sich quer zu den magnetischen Feldlinien bewegt ("die Feldlinien schneidet"), wird an den Enden eine Spannung induziert.
Wird der Leiter bewegt, so bewegen sich auch die darin befindlichen Ladungsträger, im Fall von Metallen die Elektronen. Auf die bewegten Ladungsträger wirkt die Lorenzkraft, wodurch die Ladungsträger parallel zum Leiter angetrieben werden: Es fließt ein Strom! Durch den Strom entsteht eine Ladungsverschiebung, welche die Spannung verursacht.
Mit der Drei-Finger-Regel kann man die Polung der gemessenen Induktionsspannung herausbekommen:
- Daumen: Bewegungsrichtung des Kabels (bewegte positive Ladungsträger)
- Zeigefinger: Feldlinienrichtung
- Mittelfinger: Stromrichtung im Leiter (der positiven Ladungsträger)
Man kann die Überlegung auch für die im Metall bewegten Elektronen anstellen. Dazu muß man einfach die linke Hand benutzen.
Versuch: Leiterschleife im Magnetfeld
- Aufbau
Ein Ringmagnet oder ein Rechteckmagnet stellt ein starkes, relativ homogenes Magnetfeld zur Verfügung.
- a1) Die Schleife wird senkrecht zum Magnetfeld eingetaucht und wieder herausgezogen.
- b1) Die Schleife wird senkrecht zum Magnetfeld festgehalten und dann durch Ziehen/Drücken am Kabel verkleinert oder vergrößert.
- ab2) Die Schleife wird parallel zum Magnetfeld gehalten und a) / b) wird wiederholt.
- c) Die Schleife wird im Magnetfeld gedreht.
- d) Man dreht die Schleife um 180° und wiederholt die Versuche a) b) c).
- e) Man formt eine oder mehrere zusätzliche Wicklungen zur Schleife und wiederholt die Versuche a) b) c).
- Folgerung
Ändert sich die "Anzahl der Feldlinien" durch eine Leiterschleife, so wird an den Enden der Schleife eine Spannung induziert.
Die Änderung der "Feldlinienanzahl" kann man erreichen durch:
- Eintauchen oder Herausziehen aus dem Magnetfeld
- Änderung der Schleifenfläche
- Drehen der Schleife
Versuch: Magnetfeld in einer Leiterschleife
- Aufbau
Ein langes Kabel wird mit beiden Enden an ein empfindliches Spannungsmessgerät angeschlossen. Aus dem Kabel formt man eine kleine Schleife.
- a) Dann nähert man langsam oder schnell einen Stabmagneten der Schleife und zieht ihn langsam oder schnell wieder weg.
- b) Man dreht die Schleife oder den Magneten um 180° und wiederholt den Versuch.
- c) Man hält die Schleife parallel zu den Feldlinien und wiederholt den Versuch.
- d) Man formt eine oder mehrere zusätzliche Windungen zur Schleife und wiederholt den Versuch.
- e) Man verwendet eine Spule statt der Schleife und wiederholt den Versuch.
- Folgerung
Ändert sich der zur Schleife senkrechte Anteil des Magnetfelds, so wird zwischen den Enden der Schleife eine Spannung induziert. Je schneller die Änderung, desto größer ist die Spannung. Das Vorzeichen der Spannung ist bei Abnahme und Zunahme der Feldstärke unterschiedlich und hängt von der Orientierung der Fläche zu den Magnetfeldlinien ab.
Messen der Induktionsspannung bei Veränderung der Feldstärke (magnetische Feldkonstante)
- Material
- große Feldspule (Primärspule) , kleine Induktionsspulen (Sekundärspule), Speicher-Oszilloskop, Funktionsgenerator, Messgerät
- Aufbau und Durchführung
- Eine Spule wird an einen Funktionsgenerator angeschlossen. Man kann den zeitlichen Verlauf der Spannung einstellen, die Frequenz und die Amplitude (Maximalspannung).
- Innerhalb der großen Primärspule befindet sich eine kleinere Sekundärspule.
- Sowohl die Primärspannung des Funktionsgenerators als auch die Sekundärspannung an der inneren Spule werden mit einem Zwei-Kanal-Speicher-Oszilloskop gemessen.
- Man verändert zunächst die Primärspannung, indem man die Maximalspannung, die Frequenz und den zeitlichen Verlauf variiert.
- Man zeichnet den Verlauf der Primärspannung U1 (blau) und der Sekundärspannung U2(rot) jeweils in ein Koordinatensystem:
a) Sägezahnförmiger Verlauf von U1, f=100Hz, U1max=2V
f=200Hz, U1max=2V
f=400Hz, U1max=1V
b) Sinusförmiger Verlauf von U1, f=100Hz, U1max=1V
f=100Hz, U1max=2V
f=400Hz, U1max=2V
- Das Video einer ähnlichen Messung.
- Auswertung
- Betrachtet man den zeitlichen Verlauf der Spannung, so sieht man, dass die Induktionsspannung groß ist, wenn sich die Primärspannung schnell ändert. Das bestätigt qualitativ das Induktionsgesetz.
- Um das Induktionsgesetz genauer zu überprüfen und die magnetische Feldkonstante zu messen setzt man für die Induktionsspannung an:
- [math]U_2 = n_2 \, \mu_0 \, \dot H \, A[/math]
- Dabei ist [math]n_2[/math] die Anzahl der Windungen der Sekundärspule, [math]\mu_0[/math] die magnetische Feldkonstante, [math]H[/math] die Feldstärke und [math]A[/math] die Querschnittsfläche der Sekundärspule.
- Mit Hilfe von verschiedenen Induktionsspulen kann man leicht die Proportionalität der Induktionsspannung zur Windungszahl und Fläche der Induktionsspule zeigen.
- Die Feldstärke hängt über die Stromstärke der Primärspule direkt mit der Spannung der Primärspule zusammen. Durch die Spule mit dem ohmschen Widerstand [math]R[/math] fließt ungefähr ein Strom der Stärke
- [math]I = \frac{U_1}{R}[/math].
- Für die Stärke des Magnetfeldes innnerhalb der Primärspule gilt:
- [math]H=\frac{n_1 \, I}{l} = \frac{n_1 \, U_1}{l \, R}[/math].
- Dabei ist [math]n_1[/math] die Anzahl der Windungen, [math]I[/math] die Stromstärke und [math]l[/math] die Länge der Primärspule.
- Für das Induktionsgesetz ergibt sich:
- [math]U_2 = n_2 \, \mu_0 \, \frac{n_1 \, \dot U_1}{l \, R} \, A[/math]
- Man muss also die Proportionalität der Induktionsspannung zur zeitlichen Änderung der Primärspannung zeigen.
a) Mit der Sägezahnspannung
- Man misst die zeitliche Änderung der Primärspannung, daraus die zeitliche Änderung von H. Und mit den Spulendaten die Feldkonstante.
b) Mit der Sinusspannung
- Der Spannungsverlauf in der Primärspule ist allgemein: [math]U_1 = \hat U \, \sin(2\pi \, t)[/math]. Der von b1) lautet zB: [math]U_1(t) = 1{\rm V} \, \sin(2\,\pi\,{\rm 100Hz}\, t)[/math]
- Für die Induktionsspannung bei sinusförmigen Velauf gilt: [math]U_2(t) = 2\pi\, f\, n_1\, n_2\, A\, \frac{\hat U_1}{R \, l}\cos(2\pi\,f\,t)[/math]
|
Das Induktionsgesetz lautet hier:
Dabei ist n die Anzahl der Windungen und A die Querschnittsfläche der Spule. |
Berechnung der Induktionsspannung mit der Lorentzkraft
Die Ladungsträger im Leiter werden durch die Lorentzkraft in eine Richtung geschoben, wodurch sich den Enden des Leiters ein negativer, bzw. positiver Ladungsüberschuß entsteht. Dadurch ensteht im Leiter ein elektrisches Feld, das auf die Ladungsträger eine zur Lorentzkraft entgegengesetzte Kraft ausübt.
Die Ladungsverschiebung geschieht also nur solange, bis die Ladungsträger im Kräftegleichgewicht sind: Lorentzkraft und die elektrische Feldkraft auf eine Ladung [math] q [/math] sind entgegengesetzt gleich groß:
- [math] F_L = F_e[/math]
Die Lorentzkraft ist proportional zur magnetischen Feldstärke, der Ladung und der Geschwindigkeit der Bewegung.
Zur Berechnung der elektrischen Kraft macht man die Annahme, dass das elektrische Feld im Leiter homogen wie das eines Plattenkondensators ist:
- [math] \begin{array}{rrcll} & \mu_0 \, H \, q \, v &=& q\, E & \\ \Rightarrow & \mu_0 \, H \, q \, v &=& q \frac{U}{d} \qquad| \, \mathopen: q \\ \Rightarrow & \mu_0 \, H \, v &=& \frac{U}{d} \\ \end{array}[/math]
Das muss man nur noch nach der Spannung auflösen:
- [math]U = \mu_0 H \cdot v d [/math]
Das Produkt [math]v \, d[/math] gibt an wie schnell sich die vom Leiter überstrichene Fläche [math] A[/math] vergrößert:
- [math]A = s \, d [/math]
[math]\Rightarrow \dot A = \dot s \, d = v \, d[/math]
|
Wird ein Leiter der Länge d mit der Geschwindigkeit v senkrecht zu einem Magnetfeld der Stärke H bewegt, so beträgt die induzierte Spannung an den Enden des Leiters:
|
Das Induktionsgesetz und der magnetische Fluss für Spezialfälle
Durch Experimente haben wir drei verschiedene Möglichkeiten gefunden, um in einer Schleife eine Spannung zu induzieren:
|
a) Mit Eisenkern, ohne Feld, konstante Fläche: |
[math]U_i = \dot J \cdot A[/math] |
|
b) Ohne Eisenkern, konstante Fläche: |
[math]U_i = \mu_0 \dot H \cdot A[/math] |
|
c) Ohne Eisenkern, konstante Feldstärke: |
[math]U_i = \mu_0 H \cdot \dot A [/math] |
Der logisch folgende vierte Fall von einer Änderung der Schleifenfläche bei konstanter Polarisierung ist in der Praxis schwer durchzuführen. Man müßte die Leiterschleife innerhalb eines magnetisierten Gegenstandes verändern.
Man sieht, dass in allen Fällen die Veränderung des Produkts von Feldstärke oder Polarisierung mit der Schleifenfläche und der Feldkonstante eine Rolle spielt. Es gibt im wesentlichen an, "wieviele Feldlinien oder Magnetisierungslinien durch die Leiterschleife verlaufen" und heißt magnetischer Fluss.
|
In einer Leiterschleife wird eine Spannung induziert, wenn der magnetische Fluss [math]\Phi[/math] durch die Schleife sich ändert. Der magnetische Fluß beschreibt "die Anzahl der Magnetfeldlinien und Polarisierungslinien" durch die Fläche der Leiterschleife.
|
Diese Induktionsgesetze für spezielle Fälle reichen normalerweise völlig aus. Was dabei noch nicht berücksichtigt wurde ist, dass sich auch die Fläche und die Feldstärke gleichzeitig ändern können. In der Praxis kommt das auch selten vor, trotzdem kann man alle drei Fälle in einen zusammenfassen, indem man die magnetische Flussdichte einführt.
Die magnetische Flussdichte
Die magnetische Polarisation beschreibt den Magnetisierungszustand von Materie, wie einem Weicheisenkern, die Feldstärke beschreibt den Zustand eines Feldes. Durch die Versuche haben wir herausgefunden, dass sowohl die Änderung der Polarisation [math] \vec J[/math] als auch die Änderung der Feldstärke [math]\vec H[/math] in einer Schleife zu einer Induktionsspannung führt. Der magnetische Fluss durch die Fläche hängt sowohl von [math]\mu_0\,\vec H[/math] als auch von [math] \vec J[/math] ab. Deshalb ist es praktisch die beiden Größen zu einer neuen Größe, der magnetischen Flussdichte [math]\vec B[/math], zusammenzufassen. Dazu addiert man einfach an jedem Punkt des Raumes die beiden Größen vektoriell:
- [math]\vec B = \mu_0 \vec H + \vec J[/math]
Die magnetische Flussdichte ist ein Vektorfeld und beschreibt sowohl Eigenschaften des Feldes als auch der Materie.
In vielen Fällen, z.B. außerhalb eines Permanentmagneten, befindet sich an einem Ort nur Luft, die schlecht zu magnetisieren ist, oder gar keine Materie. Für diesen Fall ist die magnetische Flussdichte parallel zur Feldstärke und beträgt einfach:
- [math]\vec B = \mu_0 \vec H[/math]
Befindet sich ein idealer Weicheisenkern in einem Magnetfeld, so ist das Innere fast feldfrei und die magnetische Flussdichte ist einfach die magnetische Polarisation:
- [math]\vec B = \vec J[/math]
Überlagern sich die beiden Größen, so ist die vektorielle Addition nicht trivial. Das sieht man am Beispiel eines Stabmagneten.
Die Magnetisierung ist im Stabmagneten homogen. Die Polarisationslinien verlaufen vom Südpol zum Nordpol.
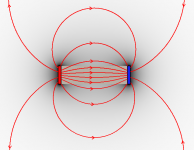
Die Feldstärke des Stabmagneten ist typisch für einen Dipol mit dem Nordpol als Quelle und dem Südpol als Senke.
Die magnetische Polarisation ist so festgelegt worden, dass die Quellenstärke des Südpols genau der Stärke der Senke der Feldstärke[1] entspricht. Um dies zu verdeutlichen, gibt es auch in der Zeichnung 12 Polarisationslinien und 12 Feldlinien.
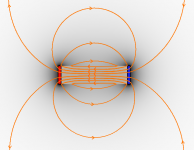
Im äußeren Bereich des Stabmagneten verlaufen die Feldstärke und die magnetische Flussdichte parallel, denn dort ist gar keine Magnetisierung.
Im Inneren des Magneten verläuft die Feldstärke im wesentlichen antiparallel zur Polarisation. Die Feldstärke ist dort aber schwächer als die Polarisation, weil sie sich ausgehend von den Polen "mehr im Raum verteilt". Deshalb ist die Summe von [math]\mu_0\,\vec H[/math] und [math]\vec J[/math] ungefähr eine Abschwächung der Polarisation und es sind nur 8 [math]\vec B[/math]-Linien gezeichnet.
Vor allem in der Nähe der Pole verläuft die Feldstärke nicht parallel zur Polarisation und ist außerdem noch stärker als in der Mitte des Magneten. Daher macht sich hier der Einfluss besonders bemerkbar und die "Polarisationslinien werden stärker in Richtung der Feldlinien gebogen".
Durch die geeignete Festlegung der Polarisation haben die [math]\vec B[/math] -Feldlinien kein Anfang und kein Ende, sie sind in sich geschlossen.
Das Induktionsgesetz und der magnetische Fluss im allgemeinen Fall
In allen drei Spezialfällen des Induktionsgesetzes ist die Induktionsspannung gerade die zeitliche Änderung des magnetischen Flusses durch die Leiterschleife. Mit der magnetischen Flussdichte kann man nun allgemein den Fluss durch eine Leiterschleife als Produkt von Flussdichte und Fläche festlegen:
- [math]\Phi = B \cdot A[/math]
Dabei ist B der zur Fläche senkrechte Anteil oder A die effektive Fläche senkrecht zu den B-Feldlinien. Will man die zeitliche Ableitung des magnetischen Flusses berechnen, so muss man ein Produkt ableiten, also die Produktregel anwenden:
- [math]U_i = \dot \Phi = \dot B \cdot A + B \cdot \dot A [/math]
Der erste Summand beschreibt die Induktionsspannung aufgrund der Veränderung von Feldstärke oder magnetischer Polarisation, der zweite Summand die Induktionsspannung aufgrund der Flächenänderung. Setzt man nun noch [math]B = \mu_0 H + J[/math] ein, so erhält man die Induktionsspannung als Summe der schon bekannten Spezialfälle:
- [math]U_i = \mu_0 \, \dot H \, A + \dot J \, A + \mu_0 H \,\dot A + J \,\dot A [/math]
|
In einer Leiterschleife wird eine Spannung induziert, wenn sich der magnetische Fluss [math]\Phi[/math] ändert:
Dabei ist B der zur Fläche senkrechte Anteil oder A die effektive Fläche senkrecht zu den B-Feldlinien. |
Versuch: Elektrisches Wirbelfeld
- Aufbau
Eine mit Neon gefüllte Glaskugel ist von einer Ringspule umgeben. Man legt eine hochfrequente (ca.10000Hz) Welchselspannung mit etwa 400 V an die Spule und erzeugt so ein sich schnell änderndes magnetisches Feld.
- Beobachtung
Video des Versuchs.
- Ergebnis
Ein geschlossener rosa Kreis entsteht innerhalb der Glaskugel. Dies lässt auf ein elektrisches Feld schließen. Da dies jedoch rund ist, kann es sich nicht um ein Potenzialfeld handeln, sondern nur um ein elektrisches Wirbelfeld.
Um ein sich änderndes Magnetfeld entsteht also ein elektrisches Wirbelfeld.
Fußnoten
- ↑ Multipliziert mit der magnetischen Feldkonstante.
Links
- Digitales Elektromagnetisches Labor (PhET Interactive Simulations, University Colorado, Boulder)
- Wikipedia: Induktives Laden
- Artikel: Induktives Laden von E-Autos (Fokus, 29.6.2016)
- Video: Versuch: Messen der Induktionsspannung mit Primär- und Sekundärspule Es wird die Proportionalität der Induktionsspannung zur Windungsanzahl, der Spulenfläche und der Änderung der Flussdichte untersucht. Die magnetische Feldkonstante wird leider nur überprüft und nicht direkt gemessen. (Von der "Experimentalgruppe Physik" im Rahmen der Seminarphase an der Beruflichen Oberschule Kempten (Allgäu). youtube: "Martin Lang")
- Kurzes Script Elektromagnetismus von "SDL-Server"
- Wikipedia: Tonabnehmer
- How Electric Guitar Pickups Work (Malcom Moore 2003)
- E-Gitarre: Nachbau des Tonabnehmers mit Schulmaterial (Peter Lingemann, Münster (Westf.))
- Leybold Mikrovoltmeter (Vs)
- Telekollek Physik 25. Folge - Elektromagnetische Induktion (Bayrischer Rundfunk)