Unterscheidung von Impuls, Energie und Kraft
(Klassische Mechanik > Impuls und Energie als Erhaltungsgrößen)
Inhaltsverzeichnis
Grundbeispiel "Kanu fahren"
Beim Losfahren drücken die Leute das Wasser mit dem Paddel nach hinten und sich nach vorne.
Die "Bewegungsmenge" wird durch den Impuls angegeben. Vor dem Losfahren haben Wasser und Boot keinen Impuls. Durch den Paddelschlag erhält das Wasser Impuls nach hinten und das Boot mit den Leuten die gleiche Impulsmenge, aber nach vorne. Wertet man Impuls nach hinten als negativ, so haben die Menschen den Impuls dem Wasser weggenommen und dem Boot gegeben.
Die Energie gibt den "Nutzwert" an. Sie kommt aus den Muskeln der Menschen und geht in die Bewegung des Bootes und des Wassers.
Die Kraft gibt an wie stark und in welche Richtung die Leute mit dem Paddel auf das Wasser drücken. Die Kraft bestimmt wie sich der Impuls des Wassers mit der Zeit ändert ("p = F t") und wie sich die Energie des Wassers längs des Weges ändert ("E = F s").[1]
|
Man benötigt Energie, um zwei Gegenstände auf unterschiedliche Geschwindigkeit zu bringen. Die Energie hat keine Richtung, der Impuls ist eine vektorielle Größe. Die Kraft auf einen Gegenstand gibt an, wie sich der Impuls mit der Zeit und wie sich die Energie längs des Weges verändert. |
Das Boot wird durch die Fahrt im Wasser gebremst, denn es schiebt das Wasser am Bug, aber auch durch die Reibung an der Bordwand, nach vorne weg.
Genauer bekommt das Wasser Impuls nach vorne und genau dieser Impuls kommt aus dem Boot.
Die Energie geht dabei von der Bewegung des Bootes auf die Wärme der Bootswand und des Wassers über.
Die Kraft auf das Boot gibt an, wie sich der Impuls des Bootes mit der Zeit und wie sich die Energie des Bootes längs des Weges ändert.
|
Zwei Gegenstände mit unterschiedlichen Geschwindigkeiten speichern Energie. Durch die Angleichung der Geschwindigkeiten wird die Energie wieder frei. |
Beispiel zur Beschreibung und Berechnung
Ein Beispiel soll klarmachen, wie man eine Bewegung mit Hilfe des Impulses, der Kraft und der Energie beschreibt. Außerdem werden einige Berechnungen ausgeführt.
Karl und Karla stehen beide auf ihrem Skateboard. Karl stößt sich von Karla ab, wodurch Karl nach links rollt und Karla nach rechts.
Karl hat eine Masse von 100kg und Karla von 50kg. Karl drückt eine halbe Sekunde lang mit einer Kraft von 60N.
Unterscheidung von Impuls, Kraft und Energie
Vor dem Losfahren haben Karl und Karla keinen Impuls. Durch das Wegdrücken bekommt Karl Impuls nach links und Karla die gleiche Impulsmenge nach rechts. Die Energie kommt aus Karl und geht in die Bewegung von Karl und Karla. Die Kraft, mit der Karl drückt, gibt an, wie sich der Impuls von den beiden mit der Zeit ändert ("p = F t") und wie sich die Energie von beiden längs des Weges ändert ("E = F s").
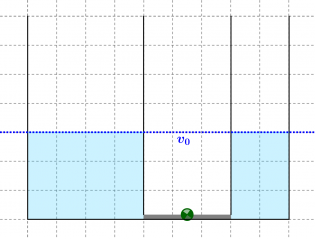
Beschreibung im Wasserbehältermodell
Der Karl entsprechende Wasserbehälter hat eine Grundfläche von 100cm2, Karlas hat nur die halbe Grundfläche[2]
Am Anfang sind sie relativ zueinander in Ruhe, deshalb steht das Wasser in beiden Behältern gleichhoch.
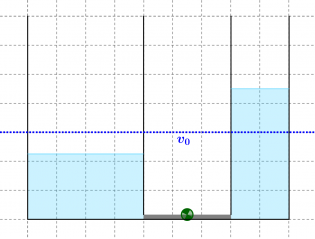
Während des Drückens werden innerhalb von einer halben Sekunde 30ml Wasser von einem Behälter weggenommen und in den anderen transportiert. (Das entspricht 60ml pro Sekunde).
Berechnung von Impuls und Energie
Beide haben die gleiche Impulsmenge, nur in entgegengesetzte Richtungen.
Die Kraft gibt gerade die zeitliche Änderung des Impulses an ([math]F=\frac{\Delta p}{\Delta t}[/math]), die Impulsmenge ergibt sich aus:
- [math]\Delta p=F\, \Delta t = 60\, \rm N \cdot 0{,}5\, s = 30\, Hy[/math].
Die Energiemenge der Bewegung hängt direkt mit der Impulsmenge und der Masse zusammen:
- [math]E_{kin} = \frac{p^2}{2\, m} \quad \left(= \frac{1}{2}\, p\, v = \frac{1}{2}\, m\, v^2 \right)[/math].
Bewegungsenergie von Karl: [math]E_{kin} = \frac{p^2}{2\, m} = \frac{(30\,\rm Hy)^2}{2\cdot 100\,\rm kg} = 4{,}5\,\rm J[/math].
Bewegungsenergie von Karla: [math]E_{kin} = \frac{p^2}{2\, m} = \frac{(30\,\rm Hy)^2}{2\cdot 50\, \rm kg} = 9\,\rm J[/math].
Karla hat doppelt so viel Bewegungsenergie wie Karl! Das liegt an ihrer kleineren Masse.
Im Wasserbehältermodell ist klar, warum: Füllt man einen breiten und einen schmalen Behälter mit jeweils der gleichen Wassermenge, so steht das Wasser in dem schmalen Behälter viel höher. Deshalb benötigt man bei dem schmalen Behälter auch mehr Energie, um die gleiche Wassermenge einzufüllen!
Berechnung der Geschwindigkeiten
Die erreichten Geschwindigkeiten kann man aus der Impulsmenge oder der Energiemenge berechnen, weil man die Masse kennt:
Aus [math]p = m\ v \quad \text{folgt}\quad v = \frac{p}{m}[/math]
Geschwindigkeit von Karl: [math]v= \frac{30\, \rm Hy}{100\,\rm kg} = 0{,}3\, \rm \frac{m}{s} = 1\, \rm \frac{km}{h} [/math]
Geschwindigkeit von Karla: [math]v= \frac{30\, \rm Hy}{50\,\rm kg} = 0{,}6\, \rm \frac{m}{s} = 2\, \rm \frac{km}{h} [/math]
Aus [math]E_{kin} = \frac{1}{2} \ m \ v^2 \quad \text{folgt}\quad v= \sqrt{ \frac{2\ E_{kin}}{m} }[/math]
Geschwindigkeit von Karl: [math]v= \sqrt{ \frac{2\cdot 4{,}5\,\rm J}{100\,\rm kg} } = 0{,}3\, \rm \frac{m}{s} = 1\, \rm \frac{km}{h}[/math]
Geschwindigkeit von Karla: [math]v= \sqrt{ \frac{2\cdot 9\,\rm J}{50\,\rm kg} } = 0{,}6\, \rm \frac{m}{s} = 2\, \rm \frac{km}{h}[/math]
Karl erreicht nur eine kleinere Geschwindigkeit als Karla, weil er träger ist. Beide haben die gleiche Impulsmenge, die bei Karl schon mit einer kleinen Geschwindigkeit erreicht werden kann, Karla muss dazu schneller sein.
Berechnung der Beschleunigungsstrecke
1. Lösungsweg
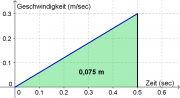
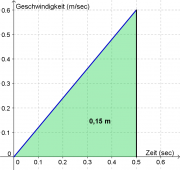
Weil man die erreichte Geschwindigkeit schon berechnet hat, kann man die Beschleunigungsstrecke aus der Fläche im Geschwindigkeit-Zeit-Diagramm bestimmen: [3]
Karls Strecke ist kürzer als Karlas, denn durch seine größere Trägheit erreicht er nur kleinere Geschwindigkeiten.
2. Lösungsweg
Um die Strecke zu bestimmen, längs der mit der bekannten Kraft beschleunigt wurde, verwendet man die bereits berechnete Energie.
Die übertragene Energiemenge ergibt sich nämlich aus "Kraft mal Weg" [math]\Delta E = F \, \Delta s[/math], was man nach dem Weg auflösen kann: [math]\Delta s = \frac{\Delta E}{F}[/math].
Beschleunigungsstrecke von Karl: [math]\Delta s = \frac{4{,}5\,\rm J}{60\, \rm N} = 0{,}075\, \rm m = 7{,}5\, \rm cm[/math]
Beschleunigungsstrecke von Karla: [math]\Delta s = \frac{9\,\rm J}{60\, \rm N} = 0{,}15\, \rm m = 15\, \rm cm[/math]
Karl wird mit der gleichen Kraft weggeschoben, erhält aber aufgrund der kürzeren Beschleunigungsstrecke weniger Energie.
Fußnoten
- ↑ Mit der gleichgroßen Kraft drückt in entgegengesetzter Richtung das Wasser auf Paddel und Boot. Wegen der gleichen Wirkungszeit sind die Impulsmengen von Wasser und Boot gleich. Aufgrund der unterschiedlichen Trägheit sind aber die Beschleunigungsstrecken nicht gleich und daher bekommen Wasser und Boot nicht die gleichen Energiemengen. Das wird am folgenden Rechenbeispiel noch genauer ausgeführt.
- ↑ In der Zeichnung ist die halbe Grundfläche durch die halbe Breite dargestellt, die Tiefe des Behälters wird dabei als konstant angenommen. Bei Behältern mit kreisförmiger oder quadratischer Grundfläche wäre dies nicht korrekt, die Breite reduziert sich dann auf [math]\frac{\sqrt 2}{2}[/math] des ursprünglichen Wertes.
- ↑ Die Fläche kann man auch mit den Bewegungsgesetzen der gleichmäßig beschleunigten Bewegung bestimmen:
- [math] s=\frac{1}{2}\, a \, t^2 \quad \text{, mit } \quad a =\frac{F}{m} [/math]