Das Huygenssche Prinzip
(Kursstufe > Mechanische Wellen)
Das nach Christiaan Huygens (1629 - 1695) benannte Huygenssche Prinzip ist eine modellhafte Vorstellung, mit der man die Ausbreitung von Wellen erklären kann:
|
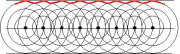
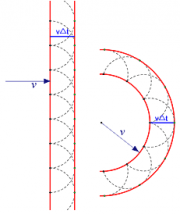
Jeder Punkt einer Wellenfront ist ein Ausgangspunkt einer neuen Kreis- oder Kugel-Welle, der sogenannten Elementarwelle. Durch Überlagerung sämtlicher Elementarwellen erhält man die sich weiter ausbreitende Wellenfront als die äußere Einhüllende der Elementarwellen. |
Bei der Ausbreitung einer ebenen Welle gehen die Elementarwellen von der ebenen Wellenfront aus und überlagern sich wieder zu einer ebenen Wellenfront. Bei der Ausbreitung einer Kugel- oder Kreiswelle ist die Einhüllende der Elementarwellen auch wieder eine kreis- oder kugelförmige Wellenfront.
Die Elementarwellen breiten sich auch gegen die Ausbreitungsrichtung der Ausgangswelle aus. Diese Anteile der Elementarwellen bleiben unberücksichtigt. Huygens konnte sich das noch nicht erklären, mittlerweile weiß man, dass sich die sich rückwärts ausbreitenden Anteile der Elementarwellen durch Interferenz auslöschen.
Mit Hilfe des Huygenschen Prinzips lassen sich die Wellenphänomene der Beugung, Reflektion und Brechung erklären.
Huygens hat zur Entwicklung seiner Vorstellung die Ausbreitung in einem Medium vorausgesetzt, wie z.B. in Wasser oder Luft. Erstaunlicherweise stimmt seine Vorstellung auch für die Ausbreitung von Licht, das sich im Vakuum ausbreitet. Denkt man an die Beschreibung des Lichts mit Lichtquanten und die Berechnung von Wahrscheinlichkeiten mit Pfadintegralen, so kann man das Huygensche Prinzip als eine Art Vorstufe davon betrachten.

Animationen
- Animation der Reflektion und Brechung einer Welle an der Grenzschicht zweier Medien.
- Konstruktion von Brechung und Reflektion mit dem Huygensschen Prinzip
Links
- LEIFI: Huygenssches Prinzip
- Wikipedia: Huygenssches Prinzip
- Spektrum: Huygenssches Prinzip
- Video: Latiniculus: Das Huygenssche Prinzip (Elementarwelle | Einhüllende | Kreiswelle | Wellenfront)
- Videovortrag: Rene Matzdorf: Huygenssches Prinzip - im Original