Mathematische Beschreibung von Schwingungen

Beschreiben der Bewegung einer harmonischen Schwingung

• Idealisierung:
  • Reibungsfrei
  • lineare Rückstellkraft

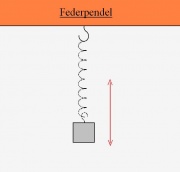
Versuch: Ein Sandpendel

Versuchsaufbau des Sandpendels(1)

Versuchsergebnis des Sandpendels(2)

Aufbau:

Siehe Bild 1

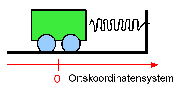
Beobachtung:

Es entsteht eine Wellenlinie. (Siehe Bild 2)

Erklärung

Diese Wellenlinie ist gerade das Zeit-Ort Diagramm einer Schwingung, denn sie gibt an wann der Körper wo ist. Die Ortsfunktion scheint eine Sinusfunktion zu sein, an der man die Amplitude und die Periode ablesen kann.

Versuch: Projektion der Kreisbewegung

Aufbau:

Versuchsaufbau Projektion der Kreisbewegung(3)

Siehe Bild 3

Beobachtung:

Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text

Erklärung

Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text

Zu 108.2

[math]\omega[/math]: Winkelgeschwindigkeit [math]f[/math]: Umläufe pro Zeit

z.B.:

[math]f = 2Hz[/math]

[math]w = 2*\pi*\left( \frac{1}{s} \right)= 4*\pi*\left( \frac{1}{s} \right)[/math]

[math]\Rightarrow \omega=2*\pi*f[/math] und weil [math]f=\left( \frac{1}{T} \right)[/math]

[math]\omega=\left( \frac{2*\pi}{T} \right)[/math]

Zu 108.3

[math]\phi_0[/math] = Phasenverschiebung

[math]\phi_0[/math] = 0° = Schwingung in Phase

[math]\phi_0[/math] =[math]\pi*(180°)[/math] = gegenphasig

Berechnung des Geschwindigkeitsgesetzes

[math]v=\dot s[/math] [math]v(t)=[\hat y*sin(\omega*t)][/math] [math]\rightarrow[/math] Ableitung = [math]v=\^y*cos(\omega*t)*\omega[/math]

Anmerkung: Elongation ist nicht von der Zeit abhängig, daher wird hier nicht abgeleitet;

Wiederholung: [f(g(t))]= f'(g(t))*g'(t)

[math]\Rightarrow[/math] [math]v(t) = \hat y*\omega*cos(\omega*t)[/math]

[math]v(t) = \hat v*cos(\omega*t)[/math]

[math]\hat v[/math] ist die maximale Geschwindigkeit

Berechnung des Beschleunigungsgesetzes

Beschleunigung = [math]a=\dot v = [\hat y*\omega*cos(\omega*t)]= \hat y*\omega*(-sin(\omega*t)*\omega[/math]

[math]\Rightarrow a(t)=-\hat y*\omega^2*sin(\omega*t)[/math]

Beispiel: Federpendel

Federpendel

Für 10 Schwingungen: 12s

Amplitude: 9cm

[math]T=1{,}2[/math]

[math]\omega=\left( \frac {2*\pi}{1{,}2} \right)[/math]

[math]s(t)=9cm*sin(\left( \frac {2*\pi}{1{,}2s} \right)*t[/math]

[math]v(t)=9cm*\left( \frac {2*\pi}{1{,}2s} \right)*cos(\left( \frac {2*\pi}{1{,}2s} \right)*t)[/math]

[math]\hat v = 9cm*\left( \frac {2*\pi}{1{,}2s} \right)= 47\frac{cm}{s}[/math]

Differentialgleichung einer harmonischen Schwingung

Die Ausgangssituation.

Zusammenhang von Ort und Rückstellkraft.

• Man betrachtet eine vereinfachte Situation: Ein Körper wird als punktförmige Masse idealisiert, die an einer masselosen, hookschen Feder befestigt ist und sich reibungslos bewegen kann.
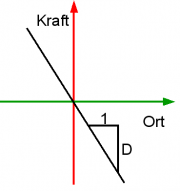
• Die äußere Situation wird durch den Zusammenhang von Ort y und Kraft F gegeben. (Wo wirkt welche Kraft?)

Bei einer hookschen Feder ist die Kraft proportional zur Auslenkung. Die Proportionalitätskonstante ist die Federhärte D. Die Rückstellkraft wirkt immer entgegen der Elongationsrichtung, es gilt also: [math]F=-Dy[/math]

• Wir suchen nun Bewegungen des Körpers in der Zeit, also den Zeit-Ort-Zusammenhänge y(t), die in diesem Kraftverlauf möglich sind.
• Die Lösung liefert uns das Newtonsche Axiom [math]F=\dot p = m a = m \ddot y[/math]. Es beschreibt nämlich den Zusammenhang zwischen Kraftverlauf und zeitlichen Ablauf der Bewegung!

Setzt man für die Kraft für die konkrete Situation ein, so ergibt sich:

[math]m \ddot y = -D \quad y [/math]

[math]\Rightarrow \qquad \ddot y= -\frac{D}{m} \quad y [/math]  Differentialgleichung (DGL) der harmonischen Schwingung

Wir suchen also Zeit-Orts-Gesetze, deren zweite zeitliche Ableitung ein Vielfaches von sich selbst sind!!

• Durch systematisches Probieren findet man Lösungen dieser DGL:

Mit [math]\omega = \sqrt{\frac{D}{m}}[/math]

Schwingungen mit einer beliebigen Amplitude

[math]y(t)=\hat y sin(\omega t)[/math]

Schwingungen mit einer zusätzlichen Phasenverschiebung:

[math]y(t)=\hat y sin(\omega t + \varphi_0)[/math]

Der Stillstand ist auch eine Lösung!

[math]y(t) = 0[/math]

• Für die Schwingungsdauer, bzw Frequenz folgt also:

[math]f = \frac{\omega}{2\pi} = \frac{1}{2\pi}\sqrt{\frac{D}{m}}[/math]

[math]T = \frac{1}{f}= 2\pi \sqrt{\frac{m}{D}}[/math]

Untersuchung dreier Schwingungen

• Ziel der Untersuchung ist es, das -Zeit-Orts-Gesetz [math]y(t)[/math] und damit auch die Frequenz der Schwingung aus der äußeren Situation, wie z.B. die Masse eines Körpers herzuleiten.

Dazu ist es sinnvoll jeweils die DGL aufzustellen. Zunächst muss man ein Koordinatensystem wählen und den Ort-Kraft-Verlauf bestimmen. Vor allem beim Fadenpendel hilft auch ein Blick in ein Buch oder ins Internet weiter.

Als Ergebnis sollen Sie sowohl eine allgemeine Formel erstellen, sowie eine konkrete Rechnung mit den gemessenen Größen durchführen.

• Welche Schlussfolgerung können Sie aus der allgemeinen Lösung ziehen? (Z.B. Abhängigkeit von der Masse, etc.)

• Vergleichen Sie dann die errechnete Frequenz mit der gemessenen und führen Sie eine Fehlerrechnung durch.

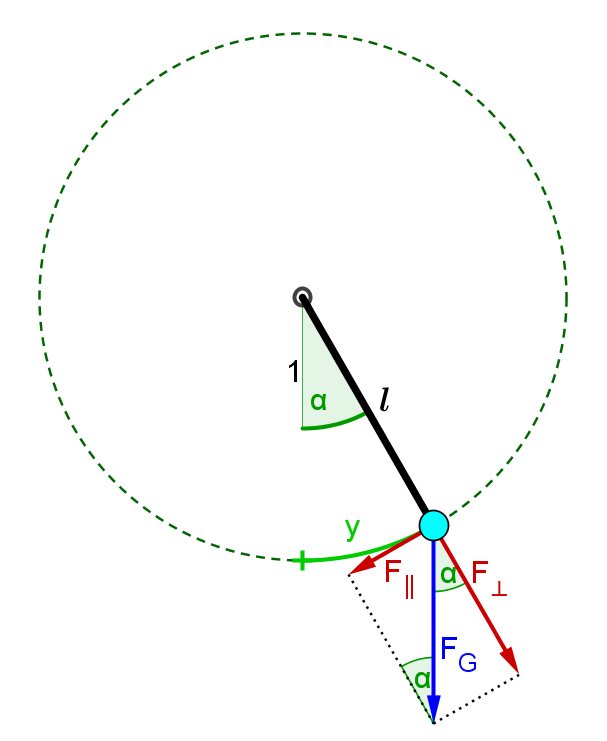
Das Fadenpendel

[math]F_{II}=-mg*sin(\phi)[/math]

da: [math]y=\phi*l[/math]

[math]F_{II}=-mg*sin((1/l) * y)[/math]

[math]F_{II}=-m*\ddot y[/math]

[math]\ddot y=g*sin((1/l) * y)[/math]

Schwingendes Wasser im U-Rohr

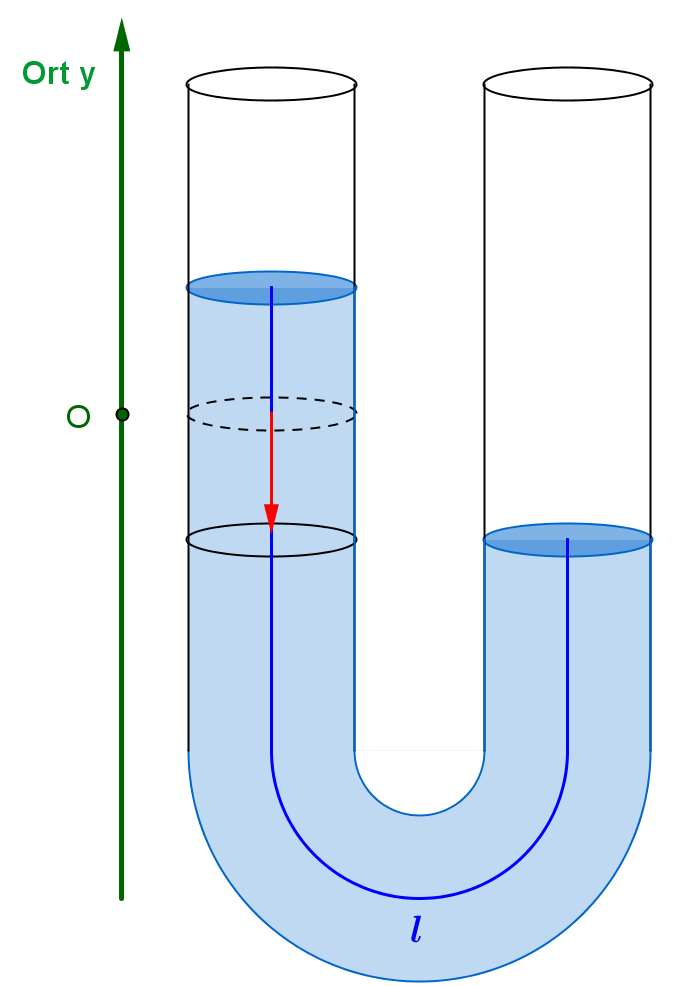
Versuchsaufbau Schwingendes Wasser im U-Rohr

Federpendel im Gravitationsfeld

Versuchsaufbau Federpendel

Der Ursprung des Koordinatensystem entspricht bei a) dem Ende der entspannten Feder. Bei Abbildung b) entspricht der Ursprung der Ruhelage des Pendels. Sowohl bei a), als auch bei b), hängt die Masse m an der Feder

Daraus ergibt sich die Differentialgleichung zweiter Ordnung:

[math]\ddot y=-D/my [/math]

mit der Lsg:

[math]\sin(\sqrt{D/m}t)[/math]

woraus man auf die vollständige Zustansvorschrift [math]y[/math] schliessen kann:

[math]y=\hat y\sin(wt)[/math] => [math]y=\hat y\sin(\sqrt{D/m}t)[/math]