Die Bewegungsmenge: Impuls und Drehimpuls
Aus Schulphysikwiki
Version vom 20. Mai 2011, 21:23 Uhr von Patrick.Nordmann (Diskussion | Beiträge)
Inhaltsverzeichnis
Massenträgheit (1. Newtonsches Axiom)
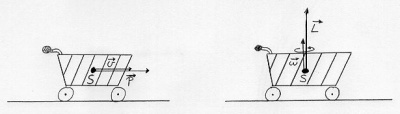
- Ein Körper behält seinen Bewegungszustand bei, solange keine Kraft auf ihn wirkt. Der Bewegungszustand wird durch die Menge an Impuls [math]\vec p[/math](Schwung) für die Translation und Drehimpuls [math]\vec L[/math] (Drehschwung) für die Rotation angegeben. Sowohl Impuls als auch Drehimpuls haben eine Richtung und sind vektorielle Größen.
- In der Schulphysik wird die Rotation von Gegenständen in der Regel vernachlässigt, man betrachtet nur die Translation.
- Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht.
Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn.
(Dreh-)Impuls als Bewegungszustand
- Jede Bewegung eines Körpers kann man als eine Überlagerung einer Translation im Raum und eine Drehung in sich beschreiben.
- Der Impuls oder Schwung [math]\vec p[/math] eines Gegenstandes beschreibt den Bewegungszustand der Translation.
- Der Drehimpuls oder Drehschwung [math] \vec L[/math] eines Gegenstandes beschreibt den Bewegungszustand der Rotation.
- Der (Dreh)impuls ist eine vektorielle Größe. Er gibt an, wieviel (Dreh)schwung ein Gegenstand hat, also wieviel "Bewegungsmenge" in dem Körper steckt. Ausserdem gibt er an in welche Richtung er sich bewegt, bzw. um welche Achse er sich dreht.
- 5:35 Rotationsveränderung durch Änderung des Trägheitsmomentes ("Pirouette")
- Bewegungsanalyse Salto vorwärts (Leistungskurs Sport von Rolf Dober)
Trägheitsgesetz (1. Newtonsches Axiom
Jeder Gegenstand behält ohne Krafteinwirkung seinen (Dreh-)Impuls in Menge und Richtung.
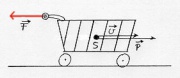
Veränderungsgesetz (2. Newtonsches Axiom)
Es ist eine Kraft nötig, um die Richtung oder die Menge des (Dreh-)Impulses zu verändern.
- Video eines hängenden Fahrradrades) (Bicycle Wheel Gyroscope) von Saint Mary's University Physics & Astronomy