Aufgaben zu Schwingungen (Lösungen)

Schaukeltier II

Große Kinder haben eine größere Masse, wodurch sie "langsamer", also mit einer geringeren Frequenz, schwingen!

Schaukeltier III

Beim Anschubsen müssen die Kinder im richtigen Rythmus, nämlich in der Eigenfrequenz anregen, sonst nimmt die Schwingung die Energie nicht an und der Effekt ist gering! Zu schnelles Anschubsen bringt also nichts.

Schwingungskategorien

Da finden sich im Kapitel Energiezufuhr bei Schwingungen Beispiele.

Schwingmännchen

Dazu muss man die Federhärte vervierfachen, also ein Viertel der Feder benutzen, oder die Masse vierteln.

Schwingmännchen II

Es gilt:	[math]\omega = 2\ \Pi \ f=\sqrt{\frac{D}{m}}[/math]	[math]E=\frac{1}{2}\, m \ (\omega \hat y)^2 = \frac{1}{2}D\ \hat y^2[/math]
*die Federkonstante verdoppelt:	Die Frequenz erhöht sich um den Faktor [math]\sqrt{2}[/math].	Der Energiegehalt verdoppelt sich.
*die Masse verdoppelt:	Die Frequenz verringert sich um den Faktor [math]\sqrt{2}[/math].	Der Energiegehalt bleibt gleich! (Das Männchen ist zwar schwerer, schwingt aber dafür langsamer.)
*die Amplitude verdoppelt:	Die Frequenz bleibt gleich!	Der Energiegehalt vervierfacht sich.

Schwingmännchen III

Das Männchen bringt 200g auf die Waage und verlängert beim Dranhängen die vorher unbelastete Feder um 40cm.

• Wieso beträgt die Federkonstante (D) gerade 1/20 N/cm = 0,05 N/cm?

Die Gewichtskraft von 100g beträgt ca. 1 Newton. ([math]F_G = m \ g = m \ 9,81 \frac{N}{kg}[/math]

[math]D=\frac{Kraft}{Verlängerung}=\frac{2N}{40 cm}[/math]

• Mit welcher Frequenz wird das Männchen schwingen?

Mit [math]\omega ^2 = \frac{D}{m}[/math] folgt:

[math]f = \frac{1}{2 \ \Pi }\sqrt{\frac{D}{m}}= \frac{1}{2 \ \Pi } \sqrt{\frac{5 N/m}{ 0,2 kg}}\approx 0,796 Hz [/math]

Es schwingt etwas weniger als einmal pro Sekunde.

Schwingmännchen IV

• Wo ist das Männchen nach 1,6 Sekunden und wie schnell ist es?

[math]y(1,6 sec) = 5cm sin(3Hz 1,6sec) \approx 5cm \ (-1) = -5cm[/math]

Das Männchen ist fast am unteren Umkehrpunkt!

[math]v(t)=\dot y(t)=5 cm \ 3 Hz \cos(3 Hz \ t) = 15 \frac{cm}{sec}\cos(3 Hz \ t)[/math]

[math]v(1,6 sec)=15 \frac{cm}{sec}\cos(3 Hz \ 1,6 sec) \approx 15 \frac{cm}{sec}\cdot 0,1 = 1,5 \frac{cm}{sec}[/math]

Dort bleibt es annähernd stehen.

• Wie groß sind Amplitude, Frequenz und Periodendauer?

[math]\hat y = 5cm[/math]

[math]2 \ \Pi \ f = 3 Hz \Rightarrow f \approx 0,48 Hz[/math]

[math]T=\frac{1}{f}\approx 2,1 sec[/math]

• Wie schnell ist das Männchen maximal?

[math]\hat v = 15 \frac{cm}{sec}[/math]

Eine "Schwingungswaage"

• Erläutern Sie, warum man mit dieser Waage die Masse der Astronautin bestimmen kann.

Mit dieser Waage kann die Trägheit, also die träge Masse der Astronautin gemessen werden. Die wirkenden Kräfte (und damit die Impuls änderung) sind durch die Versuchsanordnung vorgegeben, verändern sich also nicht. Bei einer größeren Masse wird sich daher die Geschwindigkeit weniger schnell verändern, was sich in einer niedrigeren Frequenz der Schwingung äußert.

In einem Modellversuch schwingt ein Wagen zwischen zwei Federn. Die Federkonstante einer Feder beträgt D= 3 N/m. Zusammen wirken sie wie eine Feder mit der doppelten Federkonstante. Der Wagen hat eine Masse von 190,6g.

• Wie schwer ist die Batterie, wenn der Wagen mit ihr nun in 5,6 Sekunden viermal schwingt?

Löst man die Formel für die Frequenz einer harmonichen Schwingung nach der Masse auf, so erhält man:

[math]f = \frac{1}{2 \pi}\sqrt{\frac{D}{m}} }\quad \Rightarrow \quad m= \frac{D}{4 \pi^2 \, f^2}[/math]

Mit [math]f = \frac{4}{5,6 \rm \, sec} = 0,714 \,\rm Hz[/math] folgt:

[math]m= \frac{2\cdot 3 \,\rm N/m}{4 \pi^2 \, (0,714 \,\rm 1/sec)^2} = 0,298\, \rm kg[/math]

Das ist die Masse des Wagens und der Batterie zusammen. Die Batterie hat also eine Masse von [math]298\, \rm g - 190,6 \, \rm g \approx 107 g[/math]!

Wackelnder Rückspiegel

• Ich kann die Frequenz verändern, also langsamer oder schneller fahren.
• Ich kann die Eigenfrequenz des Spiegels ändern, indem ich z.B. seine Masse vergrößere. (Das könnte man mit Knete oder einer Wäschklammer erreichen, dann verringert sich die Eigenfrequenz.)
• Ich kann den Spiegel dämpfen und ihm die Energie entziehen, z.B. indem ich mit dem Finger dranfasse. (Das ist die einzige Lösung, die dauerhaft bei allen Geschwindigkeiten funktioniert.)

harmonische Schwingung

Das kann man im Kapitel Die_harmonische_Schwingung lesen.

Zeigermodell

Der Versuch ist im Wiki unter im Kapitel Zeigerdarstellung beschrieben, aber besser im Heft!

Energie

Geg:[math]m = 1kg[/math]

[math]T = 1s[/math]

[math]\hat y = 0,01m[/math]

Ges: [math]E[/math]

Rechnung:

[math]E_{kin}=0.5*m*(\omega\hat y)^2[/math] ist unsere Formel für die kinetische Energie. Mit [math]\omega = 2\pi *f[/math] ergibt sich:

[math]E_{kin}=0.5*1kg \ (2\pi \ 1Hz \ 0.01 m)^2 \approx 0,002 \frac{kg \ m^2}{sec^2}= 0,002 Joule[/math]

Das ist sehr wenig!

Energie II

Wie muss ein Körper der Masse 1kg schwingen, damit die Schwingung 1J Energie hat?

Dazu muss man eine Frequenz und eine Amplitude finden. Je größer Frequenz und Amplitude, desto mehr Energie ist in der Schwingung.

Es soll also gelten:

[math]E = \frac{1}{2} \ 1kg (2 \ \Pi \ f \ \hat y)^2 = 1 J[/math]

Multipliziert man die Gleichung mit 2 folgt für die Frequenz und die Amplitude:

[math](2 \ \Pi \ f \ \hat y)^2 = 2 \frac{m^2}{sec^2}\qquad.[/math] Nun noch die Wurzel ziehen:

[math]\Rightarrow 2 \ \Pi \ f \ \hat y = \sqrt{2} \frac{m^2}{sec^2}[/math]

[math]\Rightarrow \ f \ \hat y =\frac{\sqrt{2}}{2 \ \Pi} \frac{m^2}{sec^2} \approx 0,225 \frac{m^2}{sec^2}[/math]

Für eine Frequenz von 1 Hz ergibt sich eine Amplitude von 0,23 m = 23 cm. Für eine Amplitude von nur 1cm = 0,01 m benötigt man schon eine Frequenz von ca 23 Hz.

Energie III

Zwei gleichschwere Körper schwingen mit der gleichen Amplitude, aber der eine doppelt so schnell wie der andere. Vergleichen sie die Energiemengen.

Für die Energie gilt: [math]E=\frac{1}{2} \ m \ (\omega \ \hat y)^2 = \frac{1}{2} \ m \ (2 \ \Pi \ f \ \hat y)^2[/math]

Die Energie ist also proportional zum Quadrat der Frequenz. Bei einer Verdoppelung wird sich der Energiegehalt vervierfachen!

8 Wasserstoffmolekül

Ein H₂-Molekül kann man idealisiert als zwei, mit einer Feder verbundene, Körper auffassen. Durch eine Messung regt man das Molekül zum Schwingen an und bestimmt die Frequenz der Schwingung zu 9,2 10¹¹ Hz.

Bestimmen sie die "Federkonstante" der gedachten Feder zwischen den Molekülen. Wieviel Energie steckt im Molekül, wenn beide Atome mit einer Amplitude von 10^-10m schwingen?

Man betrachte erst die Hälfte des Versuchsaufbau.

geg: T=1/(9,2*10^11) s m=(2/(6*10^23)*0,001)kg s=10^-10

Formel: D=m/((T/2PI)^2)

=>D=0,05599

E=D/2*ý^2

Schwieriges und Anderes

1 Schwebung

Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz. Schätzen Sie die Frequenz der anderen Stimmgabel ab.

Lösung:
Das Schätzen der Frequenz der anderen Stimmgabel wäre aüßerst schwierig, da die Frequenz wohl viel zu hoch wäre. Man kann aber die Frequenz der Schwebung abschätzen. In unserm Beispiel ergab dies etwa [math]1{,}2[/math]Hz. Da die Frequenz der zweiten Stimmgabel geringer seien wird, als die der anderen (der Reiter verlangsamt die Schwingung, indem er zusätzliche Masse einbringt) und die Frequenz der Schwebung gerade die Differenz der Frequenzen der beiden Stimmgabeln ist, ergibt sich:
[math]440Hz-xHz=1{,}2Hz\Rightarrow x=438{,}8[/math]
Die zweite Stimmgabel hat also etwa die Frequenz [math]438{,}8[/math]Hz.

2 Überlagerung

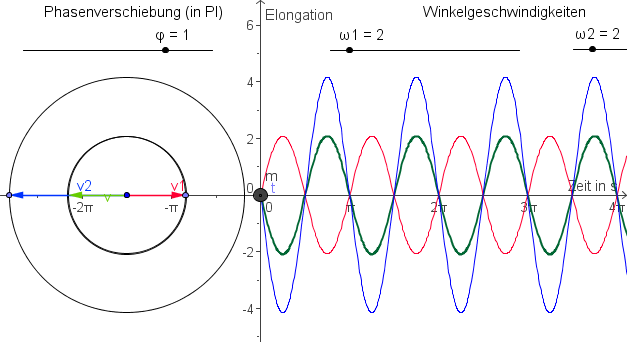
Bestimmen Sie jeweils die Schwingung, die aus der Überlagerung von y₁ und y₂ entsteht mit Hilfe des Zeigerdiagramms:

[math]y_1 = 2cm \, sin(2t)\qquad y_2 = 4cm sin(2t+\pi)[/math]

Überlegung:
Beide Schwingungen haben die selbe Frequenz (das [math]\omega[/math] beider Schwingungen ist 2)
Die zweite Schwingung ist um [math]\pi[/math] phasenverschoben, also genau gegenphasig.
Da die Schwingungen gegenphasig sind eleminieren sie sich gegenseitig, da die zweite Schwingung aber die doppelte Amplitude der ersten Schwingung hat, wird ein Ton mit der halben Amplitude der zweiten Schwingung, aber ohne Phasenverschiebung zu dieser hörbar sein.
Die mathematische Beschreibung einer solchen Schwingung wäre:
[math]y = 2cm sin(2t+\pi)[/math]

[math]y_1 = 2cm \, sin(2t)\qquad y_2 = 4cm sin(2t+\pi/2)[/math]

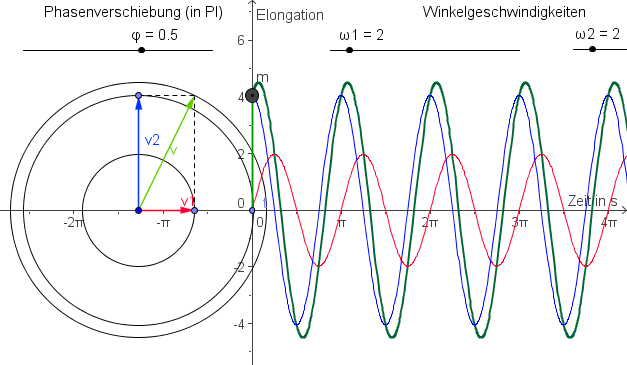
Überlegung

[math]y_1 = 2cm \, sin(2t)\qquad y_2 = 2cm sin(2t+\pi)[/math]

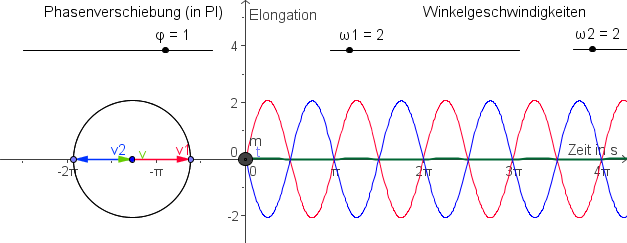
Überlegung
Da die Pfeile entgegengesetzt sind, ergibt die Amplitude 0. Daher gilt [math]y''=0[/math].

7 Schwingung bei bekannter Energie

Zwei Wagen, die beide eine Masse von 600g haben, sind mit einer Feder der Härte 1N/cm verbunden. Wie schwingen die Wagen, wenn ihnen eine Energie von 1Joule zugeführt wird?

[math]Geg:[/math]       [math]m=0.6kg[/math]     [math]D=100[/math][math]N\over m[/math]     [math]E=1J[/math]

Die Charakteristik einer Schingung definieren wir als Angabe von der Frequenz [math]f[/math] und der Amplitude [math]\hat y[/math].
Es wird mit der doppelten Federstärke [math]D[/math] gerechnet, da wir denn Fall auf nur einen Wagen idealisieren (Stille Annahme: Symmetrie der Bewegung).
Zunächst widmen wir uns der Frequenz [math]f[/math]:

[math]f=[/math][math]{\omega}\over 2\pi[/math][math]=[/math][math]\sqrt {2D \over m}\over 2\pi[/math][math]=[/math][math]\sqrt {{200 {N\over m}} \over 0.6kg}\over 2\pi[/math][math]=[/math][math]2.91Hz[/math]

Nun zur Amplitude [math]\hat y[/math]:

[math]E_{pot}=[/math][math]2\left({2D\over 2}{\hat y}^2\right)[/math]

[math]\hat y=[/math][math]\sqrt {E\over 2D}[/math][math]=[/math][math]\sqrt {1Jm\over {200N}}[/math][math]=[/math][math]{0.1\over{\sqrt 2}}m[/math][math]=[/math][math]0.07m[/math]   (für einen einzelnen Wagen; das Gesamtsystem hat jedoch 2[math]\hat y[/math])

9 E_kin = E_Spann

Die Energieformen eines (horizontalen) Federpendels in Abhängigkeit vom Ort.

Es wird gefragt für welche Auslenkung die Energie gleichermaßen in dem Impuls als auch in der Feder ist. Also wann die kinetische Energie gerade gleich der potentiellen bzw.der Spannenergie ist.

Bei der gleichmäßigen Verteilung der Energie auf die Bewegung und die Feder, enthält sowohl die Feder als auch die Bewegung gerade die Hälfte der Energie:

[math]E_{pot}= \frac{1}{2}\, E_{ges}[/math]

[math]\frac{1}{2} \, D\, y^2 = \frac{1}{2}\,\frac{1}{2} D \, \hat y^2[/math]

nach y aufgelöst:

[math]y=\frac{1}{\sqrt{2}} \, \hat y \approx 0,7 \, \hat y[/math]

Bei ca. 70% der Amplitude ist die Energie gleichmäßig auf Bewegung und Feder verteilt.

10 Zeitlicher Mittelwert von E_kin und E_Spann

Bestimmen sie das zeitliche Mittel der kinetischen und potentiellen Energie (Spannenergie der Feder) eines (horizontalen) Federpendels an einem selbst gewählten Beispiel.