Interferenz; Überlagerung von Wellen

Wenn zwei Wellen an einem Ort aufeinandertreffen, so überlagern sie sich ungestört. Dieses Phänomen nennt man Interferenz. An jeder Stelle überlagern sich zwei Schwingungen, was man durch die Addition der zwei Amplituden, bzw. Zeiger beschreiben kann.

Je nach Frequenz und Phasenverschiebung können sich die Schwingungen aufheben oder verstärken. Dabei ändert sich die räumliche Energieverteilung.

Beispiele

• Gleichzeitiges Reden wäre nicht möglich, wenn sich die Wellen gegenseitig "stören" würden.

• Wasserwellen durchdringen sich ungestört: Video von fallenden Tropfen

• Zur Schalldämpfung kann man einen Kopfhörer aufsetzen, indem ein "Gegenschall" gesendet wird. Ein Mikrophon nimmt das Signal am Ohr auf und berechnet in Echtzeit den nötigen "Gegenschall".
  • Zum Glück noch auf youtube: Video Planet Wissen - "Lärm" Wenn Töne weh tun - 1.4 WDR (Ab 1:00 min)

Leider nur noch als Textvon der ARD: Video: Gegenschall als Lärmschutz( - W wie Wissen - ARD youtube channel)

• • Wikipedia: Antischall

• Sonnenlicht ist eine Überlagerung aus elektromagnetischen Wellen. Das Spektrum umfasst einen Wellenlängenbereich von Infrarot über sichtbares Licht bis Ultraviolett. Derartige Spektren bezeichnet man auch als kontinuierlich.

Zwei-Quellen-Interferenz

Versuch: Zwei Lautsprecher

Sinusgenerator mit zwei Lautsprechern

Aufbau

Man schließt zwei Lautsprecher parallel an einen Sinusgenerator. Alternativ kann man auch mit dem Computer und einer fest installierten Stereoanlage arbeiten. (Z.B. mit Audacity)

Danach läuft man im Raum herum und hört sich den Ton an.

Man wiederholt den Versuch mit verschiedenen Tonhöhen und, falls möglich, mit verschiedenen Abständen zwischen den Lautsprechern.

Beobachtung

Beim Durchschreiten des Raumes hört man den Ton in unterschiedlichen Lautstärken, die einigermaßen rythmisch wechseln. Erhöht man die Frequenz (Tonhöhe) so liegen Orte mit geringer Latstärke näher beisammen, verkleinert man den Abstand zwischen den Lautsprechern, so sind sie weiter auseinander.

Versuch: Zwei Wasserkreiswellen

Aufbau

In einer Wellenwanne werden zwei Kreiswellen mit gleicher Frequenz erzeugt. Durch die Lichtbrechung an der unebenen Wasseroberfläche sieht man die Wellenfronten ("Berge und Täler") der Welle als dunkle und helle Streifen.

Die Wellenwanne

Detail

Beobachtung

• Video Zwei Steine in den Teich werfen (Youtube: Überlagerung und Interferenz zweier Kreiswellen von rastelli43)

• 
• 
• 
• 
• 
• 
• 
• 

Erklärung

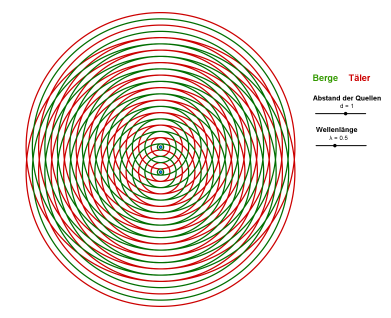
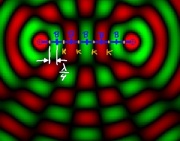
Wie kann es sein, dass die "Lautstärke" des einen Lautsprechers zusammen mit der anderen "Lautstärke" an manchen Orten nicht mehr, sondern weniger wird? Schließlich müßte dort ja auch doppelt soviel Energie vorhanden sein! Die beiden (Kugel-) Wellen überlagern sich. An jedem Punkt des Raumes summieren sich zwei Schwingungen zu einer Gesamtschwingung, was sich durch die Addition der beiden Amplituden (bzw. der Zeiger) beschreiben läßt. Je nach Überlagerungssituation wächst oder sinkt die Amplitude, der Ton wird lauter oder leiser. Treffen an einer Stelle immer zwei Berge oder zwei Täler aufeinander, so verdoppelt sich dort die Amplitude. Das nennt man konstruktive Interferenz. Die Zeiger zeigen in die gleiche Richtung, es gibt keine Phasenverschiebung. Trifft ein Berg auf ein Tal oder ein Tal auf einen Berg, so ist die Summe der Amplitude Null. Das nennt man destruktive Interferenz. Die Zeiger zeigen in entgegengesetzte Richtungen. Die Phasenverschiebung beträgt dann [math]\Pi[/math] oder 180°. Legt man zwei Folien mit konzentrischen Kreisen aufeinander ergibt sich ein ähnlicher, sogenannter "Moiré-Effekt". Man kann so gut nachvollziehen wo die Stellen mit konstruktiver oder destruktiver Interferenz liegen. Bei dieser Animation kann man das auch online tun. Die hellen Streifen, bei denen sich nur grüne mit grünen und rote mit roten Kreisen schneiden, sind Stellen mit konstruktiver Interferenz. Hier ist es laut. Die hellen Streifen, bei denen sich immer ein roter mit einem grünen Kreis schneidet sind die Stellen destruktiver Interferenz. Hier ist es leise. Mit Hilfe dieses Applets von Walter Fendt kann man ebenso die räumliche Verteilung der konstruktiven und destruktiven Interferenzen untersuchen. Da hier sich die Wellen auch bewegen, sieht man auch die Ausbreitungsrichtung. Noch besser ist diese Simulation einer Wellenwanne von Paul Falstad. Stellt man "zwei Quellen mit einer Frequenz" ein, so kann man sehr gut den räumlichen und zeitlichen Verlauf der Überlagerung erkennen. Hier kann man auch gut die stehende Welle zwischen den Quellen beobachten. Dort befinden sich abwechselnd Stellen mit destruktiver und konstruktiver Interferenz. In diesem Applet von Peter Kraus kann man die Zeigeraddition gut verstehen. Um Zwei Quellen zu haben muss man "Doppelspalt" einstellen.

Animation und Kopiervorlage

Die stehende Welle in 2D.

und in 3D (Standbilder der Wellenwanne von Paul Falstad.)

Ergebnis

Durch die Überlagerung zweier Wellen ist die Intensität der resultierenden Welle nicht mehr gleichmäßig über die Wellenfront verteilt. An manche Orte wird mehr Energie transportiert als an andere.

An jeder Stelle im Raum überlagern sich zwei Schwingungen mit gleicher Frequenz aber unterschiedlicher Phase.

Zur Berechnung der Amplitude an einer Stelle kann man die beiden Zeiger addieren. Bei der Herleitung der Wellengleichung hat man gesehen, dass die Phase eines Zeigers von der Zeit und von der Entfernung zur Quelle abhängt:

[math]\varphi_1=\omega \, t - \frac{2\pi}{\lambda}\, s_1[/math]

Der Phasenunterschied zwischen den Zeigern hängt nur vom Unterschied der Entfernungen zu den Quellen ab, dem Gangunterschied [math]\triangle s = s_2 - s_1[/math]:

[math]\triangle \varphi= \frac{2\pi}{\lambda}\, \triangle s[/math]

Durch die Abnahme der Intensität mit der Entfernung von der Quelle verändern sich auch die Amplituden. Nur an Orten, bei denen der Gangunterschied Null beträgt sind die beiden Amplituden gleich. Meistens wird dieser Effekt aber der Einfachheit halber vernachlässigt und man nimmt an, dass die Amplituden gleichgroß sind.

Gangunterschied [math]\triangle s [/math]

Phasenverschiebung [math]\triangle \varphi[/math]

konstruktive Interferenz (Zeigerdiagramm der sich überlagernden Schwingungen!) [math]\triangle s = n \lambda[/math]

[math]\triangle \varphi = n 2 \pi[/math]

[math](n= 0,1,2,3,...)[/math]

destruktive Interferenz [math]\triangle s = n \lambda - \lambda / 2 [/math]

[math]\triangle \varphi = n 2 \pi +\pi[/math]

[math](n= 1,2,3,...)[/math]

Links

• wikipedia: Interferenz
• Videos von Wassertropfen und Wasserwellen (Fachinformationszentrum Chemie, Berlin)
  • Einfache Überlagerung
• Ein Applet, das eine Wellenwanne simuliert. Beeindruckend! (Von Paul Falstad.)

Zwei Quellen

• Video Zwei Steine in den Teich werfen (Youtube: Überlagerung und Interferenz zweier Kreiswellen von rastelli43)
• Applet mit Interferenz zweier Kreis- oder Kugelwellen (Walter Fendt)
• Doppelspaltsimulation von Peter Kraus (pk-applets.de)
• Zwei Quellen Interferenz (LEIFI)

Stehende Welle

• Applet LEIFI Überlagerung zweier gegenläufiger Wellen mit "Luftdruck"
• Applet der Überlagerung zweier gegenläufiger Wellenzüge zu einer stehenden Welle (Peter Kraus, pk-applets)

Gegenschall

• Zum Glück noch auf youtube: Video Planet Wissen - "Lärm" Wenn Töne weh tun - 1.4 WDR (Ab 1:00 min)

Leider nur noch als Textvon der ARD: Video: Gegenschall als Lärmschutz( - W wie Wissen - ARD youtube channel)

• Wikipedia: Antischall