Ladung als Quellenstärke und der Fluss eines Feldes
Inhaltsverzeichnis
Fragestellung
- Wie kann man bei gegebener Verteilung der Ladung (magnetische, elektrische oder schwere) die Feldstärke an einer Stelle berechnen?
Aus unseren bisherigen Erfahrungen können wir zwei qualitative Aussagen machen:
- Je kleiner der Abstand von der Ladung, desto größer die Feldstärke.
- Je größer die felderzeugende Ladung, desto größer die Feldstärke.
Beide Aussagen werden nun genauer untersucht.
Feldstärke eines Zentralfeldes
Man geht davon aus, dass man die Größe der Ladung kennt. Nun möchte man die Feldstärke an einem bestimmten Ort berechnen.
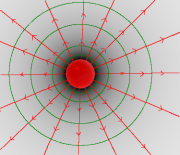
Dazu schaut man sich die graphische Darstellung eines Zentralfeldes nochmal genau an. An den Orten mit großer Feldstärke liegen die gezeichneten Linien dichter beisammen. Wie kann man das präzisieren?
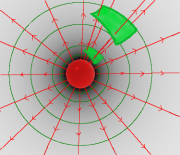
Die Orthogonalfächen haben mit zunehmendem Abstand von der Ladung eine immer größere Fläche. Die Anzahl der sie durchdringenden Linien bleibt aber immer gleich.
Als "Dichte" der Feldlinien könnte man also die "Anzahl der Linien" pro Fläche verstehen.
Feldstärke und Orthogonalflächen
Wenn die "Feldliniendichte" ein Maß für die Feldstärke sein soll, dann muß in dem Maße wie eine Fläche zunimmt, die Feldstärke abnehmen. Das soll durch eine Messung an einem Zentralfeld überprüft werden.
Wie könnte die Feldstärke abnehmen?
- Antiproportional zum Radius: Doppelter Abstand --> halbe Feldstärke
- Antiproportional zum Inhalt der Orthogonalfläche: Doppelter Abstand (Vierfacher Flächeninhalt [math]A=4 \pi r^2[/math]) --> viertel Feldstärke
Zur Überprüfung messen wir die Kraftwirkung auf einen Probenordpol im Feld des Nordpols eines langen Stabmagneten. Wir stellen fest: Verdoppelt man den Abstand der Pole, so verringert sich die Feldstärke auf ein Viertel!
Auch für das elektrische Feld kann man diesen Zusammenhang messen und findet das gleiche Ergebnis!
Für das Schwerefeld gilt dies ebenso. Schon Newton kannte diesen Zusammenhang für das Gravitationsfeld. Er ergibt sich aus der Beobachtung der Planeten.
Die Feldstärke um eine Ladung nimmt in dem Maße ab, wie der Inhalt der Orthogonalfläche zunimmt: [math]g \sim \frac{1}{A} [/math] oder [math]g \, A[/math] ist konstant "Doppelte Fläche --> Halbe Feldstärke" [math]E \sim \frac{1}{A}[/math] oder [math]E \, A[/math] ist konstant [math]H \sim \frac{1}{A}[/math] oder [math]H \, A[/math] ist konstant
Feldstärke und felderzeugende Ladung
Wieder kann man im Falle der magnetischen Ladungen relativ einfach messen. Dazu verdoppeln wir die felderzeugende Ladung des Stabmagneten, indem wir einen zweiten parallel dazu befestigen. Jetzt messen wir wieder die Kraftwirkung auf den Probenorpol.
Wir stellen fest: Bei der doppelten felderzeugenden Ladung ist die Kraftwirkung und somit auch die Feldstärke doppelt so groß!
Dieser Zusammenhang gilt auch für das schwere und das elektrische Feld. Der Mond hat zB. nur ca. 1/81 der Erdmasse. In einem Abstand von 3600 km vom Mondmittelpunkt, was dem Erdradius entspricht, ist daher auch die Kraftwirkung nur 1/81 der Erdanziehungskraft.
Die Stärke eines Feldes um einen geladenen Gegenstand ist proportional zu seiner Ladung:
[math]g \sim m \qquad E \sim Q \qquad H \sim Q_m [/math]
Feldfluß, Quellenstärke und Feldkonstanten
Die beiden Zusammenhänge zwischen Feldstärke und Flächeninhalt einerseits und Feldstärke und Ladung andererseits kann man nun zusammenfassen:
Neue, elegante Formulierung, welche die "Feldliniendichte" korrekt beschreibt.
Der Fluß eines Feldes durch eine geschlossene Fläche entspricht der enthaltenen Ladungsmenge.
[math]\mu_0 \,H \, A = Q_m[/math]
Unterscheidung: Der Fluß der Feldstärke ist eigentlich nur H A. Aber in der Physik hat sich für [math]\mu_0 \,H \, A[/math] der Begriff des magnetischen Flußes eingebürgert. Das ist eine der vielen Stolperfallen in den Bezeichnungen, die sich historisch so entwickelt haben.
Die "Dichte" der gezeichneten Linien scheint ein Maß für die Feldstärke zu sein.
Der Fluß durch die kleine und die große Fläche ist gleichgroß.
Die geringere Feldstärke wird durch weniger gezeichnete Linien dargestellt.
