Experimentelle Untersuchung einer Schaukel

Kinder beim Schaukeln

Die Schaukel am Droste.

(Kursstufe > Experimentell-induktives Vorgehen am Beispiel einer Schwingung)

Vorüberlegungen/Entwicklung eigener Fragen

Wir sind zu unserer Schaukel am Droste gegangen.

Wir haben uns ein Bild mit einem schaukelnden Kind angesehen.

"Was kann man überhaupt fragen?" Beispiele für mögliche Fragen wurden von uns gesucht, darunter:

1. Warum schaukelt eine Schaukel?
2. Wie weit kann man von der Schaukel abspringen?
3. Wie groß ist die maximale Auslenkung?
4. Welche Geschwindigkeit erreicht die Schaukel?
   1. Hängt diese von der Anzahl der Personen ab?
   2. Wie verändert sich die maximale Geschwindigkeit (Beschleunigung) beim Ausschaukeln mit der Zeit?
5. Wie wirkt sich der Anfangswinkel auf das Schaukeln aus?
6. Wie verändert sich die Höhe bei einem Schaukelvorgang?
7. Wie lange dauert das Ausschaukeln von der maximalen Auslenkung? (Bei vielen/wenigen Personen?)
8. Welche Kräfte wirken auf die Schaukel und die Personen?
9. Wie beeinflusst die Seillänge die Schaukel? (evt. ein Experiment aufbauen.)
10. Hängt die Schwingungsdauer von der Menge der Personen ab?
    1. oder von der Sitz- bzw. Stehposition?
    2. oder vom Anfangswinkel?

1. "Wieso sind die Seile gerade?"
2. "Wo kommt die Energie her?"
3. "Wie bewegt sich die Schaukel im Raum?"
4. "Wie wird die Schaukel angetrieben?"
5. "Wie viel Energie ist im physikalischen System?"
6. "Welche Kräfte wirken?"
7. "Welche Geschwindigkeit hat die Schaukel am untersten Punkt?"
8. "Wie bewegt sich die Schaukel im Raum?"
9. "Wie groß ist die Periodendauer?"
   1. "Hängt sie vom Antrieb ab?"
   2. "Hängt sie vom maximalen Ausschlag (Amplitude) ab?"
   3. "Hängt sie von der Anzahl der Personen ab?"
   4. "Ändert sich die Periode, wenn man sich stellt oder hinsetzt?"
10. "Welche Sicherheitsvorschriften gibt es?"
11. "Warum kann man nicht eine beliebige Höhe erreichen und auch keinen Überschlag machen?"

• Wie man antreibt
• Wirken von Kräften
• Beschreiben der Bewegung
• Impulsfluss
• Abhängigkeit der Bewegung
• Energiemenge/Fluss (z.B Wärme)
• Schwingungsdauer

Videoanalyse der Schaukel

	4 Personen	3 Personen	2 Personen	1 Person	ohne Personen
stehend mit Antrieb hoch	Video
stehend mit Antrieb niedrig
stehend ohne Antrieb
sitzend ohne Antrieb
leer

Direkte Messungen an der Schaukel

Periodendauer

• Wir haben jeweils 10 Perioden mit einer Handstoppuhr gemessen und dabei den Antrieb, die Amplitude, die Anzahl und Sitzposition der Leute variiert.

Die Messungen sind nicht besonders genau, geben aber einen Anhaltspunkt. Außer der ungenauen Zeitmessung ist die abnehmende Amplitude ein Problem. Denn die Periode hängt, wie wir dann herausgefunden haben, von der von der Amplitude ab und das Ergebnis wird verfälscht.

Art der Schaukelbewegung	Zeit für 10 Perioden in Sekunden
mit Antrieb; kleine Amplitude	24,47
mit Antrieb; große Amplitude	27,08
ohne Antrieb; kleine Amplitude	24,98
ohne Antrieb; große Amplitude	26,61
mit 2 Personen; kleine Amplitude	25,28
mit 2 Personen; große Amplitude	26,92
mit 2 Personen, hängend; mittlere Amplitude	27,04
mit 2 Personen, stehend; mittlere Amplitude	23,03

Ergebnisse:

• Bei allen Messungen nimmt die Periodendauer mit der Amplitude zu. Allerdings nicht proportional. Bei unseren Messungen ergibt sich Unterschied von ca. 10%.
• Im Rahmen der Messgenauigkeit ändert der Antrieb die Periode nicht.
• Bei der Abhängigkeit von der Personenanzahl haben wir leider einmal die Amplitude "mittelgroß" gewählt, dadurch ist das Messergebnis schlecht vergleichbar. Die Masse hat aber, wenn überhaupt, einen geringen Einfluss, schließlich haben wir die Masse verdoppelt!
• Je höher der Schwerpunkt, desto kürzer ist die Periode.

• ( ) Wir haben eine Videoaufnahme mit dazugehaltenem Maßstab gemacht. Den Film kann man mit einer Videoanalyse auswerten.

Entwicklung und Vereinfachung durch ein Modell

Auswählen einer leitenden Frage

Nach diesen ersten Gedanken, versuchten wir die Fülle an Fragen zu begrenzen und uns auf eine Frage zu einigen, die zum Grundverständnis der Physikalischen Abläufe einer schwingenden Schaukel am zuträglichsten sei und so vielleicht auch die anderen Fragen leichter zu beantworten seien. Diese Frage lautete: "Wovon hängt die Schwingungsdauer ab?" Da nun die leitende Frage gestellt war, mussten wir im nächsten Schritt wieder Einschränkungen in Kauf nehmen, in sofern, als dass uns nur ein sehr vereinfachtes Modell einer Schaukel zur Verfügung stand, an dem wir nun versuchen wollte Antworten zu finden.

Trotz der scheinbar nahezu idealen Bedingungen im Bezug auf Reibung, Luftwiderstand und Zuverlässigkeit des Schaukelmodells, wurde schnell klar, dass exakte Messergebnisse nie möglich sein werden, da sich die Amplitude der Schwingung relativ schnell wieder verkleinerte, nachdem man der Schaukel einen Schwingungsimpuls gab.

Mathematische Beschreibung

Trotz dieser und weiterer fast unvermeidbarer Ungenauigkeiten des Versuchs, probierte man im nächsten und letzten Schritt die Ergebnisse mathematisch zu erfassen, zu beschreiben und zu kategorisieren.

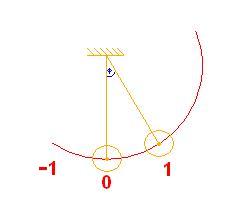
• Im roten Koordinatensystem ist eine Angabe des Ortes möglich.
• Die Auslenkung y heisst Elongation.
• Bei y=0 ist das Pendel in der Ruhelage
• Das Messen, bzw die Angabe der Elongation ist mit Hilfe des Winkels [math]\varphi[/math] möglich.
• Maximale Auslenkung: [math]\hat y[/math](Amplitude)
• Periode(ndauer) T: Zeit einer Schwingung
• Frequenz f: Anzahl Schwingungen pro Zeit [math]T=\frac{1}{f} \qquad f=\frac{1}{T}[/math]

Fazit

Der Versuch zeigte, dass von der ersten Frage bis zum Ergebnis viel Abstriche zu machen waren im Bezug auf Realitätsnähe des Versuchs/Modells sowie auf die Beweglichkeit der Fragestellung. Nur sehr explizite und genaue Fragestllungen und Herangehensweisen sind realistisch durchführbar, dies wurde einem hiermit gezeigt.

So kann man sagen,dass ein erstes und vereinfachtes Bild der physikalischen Vorgehenswiese bei der Beschreibung von physikalischen Phänomenen gewonnen war.

Untersuchungsauftrag: Wovon hängt die Frequenz der frei schwingenden Schaukel ab?

• Untersuchen Sie experimentell, wovon die Frequenz, bzw. die Schwingungsdauer einer Schaukel abhängt.

Mögliche Beeinflussungen durch:

• Schaukellänge l
• Masse m
• Amplitude [math]\hat y[/math]
• Reibung

Man muss also immer nur eine Größe variieren und dann jeweils die Periode messen. Misst man z.B. für verschiedene Amplituden die Periode erhält man einen Zusammenhang zwischen Amplitude und Periodendauer, der streng genommen nur für die gewählte Länge, Masse usw. gilt.

Ändert sich die Periode bei Variation einer Größe nicht, so ist sie davon unabhängig.

Periodenlänge eines Fadenpendels

• Vereinfachung des schaukelnden Kindes als Fadenpendel (mathematisches Pendel)
  • Die Masse wird als punktförmig angenommen, die Aufhängung als masselos.
• Weitere Vereinfachung: Ungedämpftes Pendel (Ohne Energieverlust)

Aufbau

Das Fadenpendel

Mittels einer Klemme wird eine Stange senkrecht an einem Tisch angebracht. An dieser Stange wird am oberen Ende ein Haken sowie ein Geodreieck angebracht. Das Geodreieck hat die Funktion, die Amplitude zu messen und wird daher so angebracht, dass die längere Seite oben ist und und die auf das Geodreieck aufgetragene Senkrechte genau auf der Stange verläuft.

Am Haken wird nun ein Faden befestigt, an dessen Ende ein Kugel befestigt ist. Mit dem so entstandenen Pendel werden die Versuche durchgeführt, deren Ergebnisse unten aufgeführt sind.

Zur Untersuchung der Abhängigkeit von einer Größe muß diese variiert und alle anderen konstant gehalten werden.

Beobachtung/Messwerte

Abhängigkeit von der Fadenlänge l:

Tabelle 1

 [math]m[/math] = 0,1342 kg; [math]\hat y[/math] = 30°  
 [math]l[/math]  |  10 cm  | 20 cm | 30 cm  | 40 cm  | 50 cm
 [math]T[/math] | 0,75 s |  1 s   | 1,16 s | 1,25 s | 1,47 s
 [math]T[/math] | 0,78 s |  1 s   | 1,16 s | 1,25 s | 1,5 s
 [math]T[/math] | 0,78 s | 1,03 s | 1,16 s | 1,32 s | 1,5 s
 [math]T[/math] | 0,78 s | 0,97 s | 1,16 s | 1,35 s | 1,5 s
 [math]T[/math] | 0,78 s |  1 s   | 1,16 s | 1,28 s | 1,56 s
D[math]T[/math] | 0,774 s |  1 s  | 1,16 s | 1,29 s | 1,506 s

Abhängigkeit von der Amplitude [math]\hat y[/math]:

Tabelle 2

 [math]m[/math] = 0,1342 kg; [math]l[/math] = 30 cm
 [math]\hat y[/math] |    15°  |   30°  |    45°  |   60°   |   75°   |    90°
 [math]T[/math] | 1,09 s  | 1,16 s | 1,16 s  | 1,22 s  | 1,25 s  | 1,35 s
 [math]T[/math] | 1,13 s  | 1,16 s | 1,13 s  | 1,18 s  | 1,25 s  | 1,41 s 
 [math]T[/math] | 1,09 s  | 1,16 s | 1,18 s  | 1,18 s  | 1,22 s  | 1,35 s
 [math]T[/math] | 1,13 s  | 1,16 s | 1,16 s  | 1,18 s  | 1,25 s  | 1,35 s
 [math]T[/math] | 1,09 s  | 1,16 s | 1,16 s  | 1,18 s  | 1,25 s  | 1,37 s
D[math]T[/math] | 1,106 s | 1,16 s | 1,158 s | 1,188 s | 1,244 s  | 1,366 s

Die Amplitude des Fadenpendels ist sehr stabil, nach 10 Perioden beträgt sie bei einer Startamplitude von 30° noch etwa 25°. In der Tabelle nicht aufgeführt, da für unsere Zwecke wertlos sind Extremversuche mit Startamplituden über 90° da hier die Kugel nicht auf einer stabilen Kreisbahn pendelt.

Erklärung/Auswertung

Um die Abhängigkeit von [math]T[/math] und [math]l[/math] möglichst durch eine Konstante zu definieren, werden verschiedene mathematische einfache Möglichkeiten ausprobiert:

([math]c[/math] steht für die restlichen Bestandteile der Schwingungsformel; die Rechnungen gelten für [math]\hat y=30[/math]°)

1. [math]T = l c[/math]

[math]T \over l[/math][math] = c[/math] ; [math]0,774 \over 0,1[/math][math] = 7,74[/math] ; [math]1 \over 0,2[/math][math] = 5[/math] ; [math]1,16\over 0,3[/math][math] = 3,87[/math] ; [math]1,29\over 0,4[/math][math] = 3,225[/math] ; [math]1,506\over 0,5[/math][math] = 3,012[/math]

2. [math]T = l^2 c[/math]

[math]T \over l^2[/math][math] = c[/math] ; [math]0,774 \over 0,1^2[/math][math] = 77,4[/math] ; [math]1 \over 0,2^2[/math][math] = 25[/math] ; [math]1,16\over 0,3^2[/math][math] = 12,88[/math] ; [math]1,29\over 0,4^2[/math][math] = 8,06[/math] ; [math]1,506\over 0,5^2[/math][math] = 6,02[/math]

3. [math]T = \sqrt{l} c[/math]

[math]c=[/math][math] T \over \sqrt{l}[/math] ; [math] 0,774 \over \sqrt{0,1}[/math][math]=2,45[/math] ; [math] 1 \over \sqrt{0,2}[/math][math]=2,24[/math] ; [math] 1,16\over \sqrt{0,3}[/math][math]=2,12[/math] ; [math] 1,29\over \sqrt{0,4}[/math][math]=2,04[/math] ; [math] 1,506\over \sqrt{0,5}[/math][math]=2,13[/math]

Die einzige der Formeln, deren Ergebnisse nur hinter dem Komma unterschiedlich sind, ist: [math]T = \sqrt{l} c[/math] Wir müssen also davon ausgehen, dass die Unterschiede, die bei 3. bestehen aufgrund von Messungenauigkeiten entstehen und den Durchschnitt der fünf Werte ausrechen, der da lautet: 2,2.

Wir gehen nun davon aus, dass die gesuchte Konstante be ieiner Amplitude von 30° etwa 2,2 beträgt.

Periodenlänge einer schwingenden Stange

Aufbau

Der schwingende Stab

Mittels einer Klemme wird eine Stange senkrecht an einem Tisch angebracht. An dieser Stange wird am oberen Ende ein Geodreieck sowie eine kleinere, senkrecht zur Ersten stehenden Stange befestigt. Das Geodreieck hat die Funktion, die Amplitude zu messen und wird daher so angebracht, dass die längere Seite oben ist und und die auf das Geodreieck aufgetragene Senkrechte genau auf der Stange verläuft. An der zweiten Stange wird nun erneut eine Dritte befestigt, senkrecht zur Kurzen, also parallel zur Ersten. Diese dritte Stange ist im Gegensatz zu den anderen beiden frei schwingend. Da das so entstandenen Pendel schon über ein Eigengewicht verfügt, wird auf ein zusätzliches Gewicht verzichtet. Mit dieser Konstruktion werden dann die Versuche durchgeführt, deren Ergebnisse unten aufgeführt sind. Zur Untersuchung der Abhängigkeit von einer Größe muß diese variiert und alle anderen konstant gehalten werden.

Beobachtung/Messwerte

Abhängigkeit von der Amplitude [math]\hat y[/math]:

Tabelle 1

[math]m[/math] = 1.01kg; [math]l[/math] = 1.01m  
[math]\hat y[/math] in ° |              30        / avg. |              45        / avg. |              90        / avg. |
[math]T[/math] in s | 1.67; 1.61; 1.62; 1.67 / 1.64 | 1.71; 1.72; 1.65; 1.68 / 1.69 | 1.9 ; 1.95; 1.93; 1.89 / 1.92 |

Tabelle 2

[math]m[/math] = 0.23kg; [math]l[/math] = 1.06m
[math]\hat y[/math] in ° |              30        / avg. |              45        / avg. |              90        / avg. |
[math]T[/math] in s | 1.66; 1.72; 1.7 ; 1.67 / 1.69 | 1.76; 1.73; 1.79; 1.81 / 1.77 | 1.98; 1.97; 1.95; 1.99 / 1.97 |

Tabelle 3

[math]m[/math] = 0.31kg; [math]l[/math] = 0.33m
[math]\hat y[/math] in ° |              30        / avg. |              45        / avg. |              90        / avg. |
[math]T[/math] in s | 0.98; 1.02; 0.96; 0.97 / 0.98 | 1.01; 1.04; 1.04; 1.03 / 1.03 | 1.11; 1.04; 1.11; 1.17 / 1.11 |

Während der Versuchsdurchführung können wir an unserer Stativstange ein gewisses "Mitschwingen" beobachten, im Takt zum eigentlich schwingenden Objekt.
Weiterhin ist noch hinzuzufügen, dass die maximale Elongation von Periode zu Periode um ein sehr unterschiedliches Maß abnimmt, die Differenzen werden immer kleiner. Da wir dies bei all unseren Testreihen beobachten, testen wir abgesondert den "Extremfall", eine Amplitude von 180°, um diesen Effekt zu verstärken. Hierbei können wir beobachten, dass bereits nach einer Periode die Differenz der Amplitude etwa 60° beträgt; nach der zweiten 30°, usw.

Erklärung/Auswertung

Wie aus den Tabellen 1.03 und 2 zu entnehmen ist, haben unsere Stangen eine sehr ähnliche Länge ([math]l[/math]), jedoch eine unterschiedliche Masse: Stange 2 wiegt weniger als ein Viertel von Stange 1. Hiermit können wir Johannes' anfängliche Hypothese, dass die Masse ([math]m[/math]) irrelevant sei, sehr gut untermauern. Für die einzelnen Amplituden ([math]\hat y[/math]) weichen die Perioden ([math]T[/math]) jeweils nur um ein paar Hunderstelsekunden voneinander ab. "Ein solch geringer Unterschied hat seinen Ursprung nicht in einer so großen Massenrelation von 1:4" denken wir uns; die geringfügigen Längenunterschiede und Messungenauigkeiten müssen hierfür verantwortlich sein.
An dieser Stelle kommt Stange 3 ins Spiel, mit einer dritten Länge. Somit lässt sich die Abhängigkeit der Periode von der Länge besser untersuchen: auf den ersten Blick ist klar, dass die Periode mit Zunahme der Länge ebenfalls zunimmt ([math]l \propto T[/math]?). Um die genaue Abhängigkeit herauszufinden, probieren wir gängige Verhältnisse mithilfe einer allgemeinen Formel aus:
([math]c[/math] steht für die restlichen Bestandteile der Schwingungsformel; die Rechnungen gelten für [math]\hat y=45[/math]°)

1. [math]T = l c[/math]

[math]T \over l[/math][math] = c[/math] ; [math]1.77 \over l.06[/math][math] = 1.67[/math] ; [math]1.69 \over 1.01[/math][math] = 1.67[/math] ; [math]1.03\over 0.33[/math][math] = 3.12[/math]

1. [math]T = l^2 c[/math]

[math]T \over l^2[/math][math] = c[/math] ; [math]1.77 \over 1.06^2[/math][math] = 1.56[/math] ; [math]1.69 \over 1.01^2[/math][math] = 1.66[/math] ; [math]1.03\over 0.33^2[/math][math] = 9.46[/math]

1. [math]T = \sqrt{l} c[/math]

[math]c=[/math][math] T \over \sqrt{l}[/math] ; [math] 1.77 \over \sqrt{1.06}[/math][math]=1.71[/math] ; [math] 1.69 \over \sqrt{1.01}[/math][math]=1.68[/math] ; [math] 1.03\over \sqrt{0.33}[/math][math]=1.79[/math]

Nur bei [math]\sqrt {l}[/math] sind Züge einer Übereinstimmung zu erkennen. Somit lässt sich sagen, dass sich die Wurzel der Länge proportional zur Periode verhält ([math]\sqrt l \propto T[/math]).

Versuche: Johannes Schlicksbier und Nikolaj Kulvelis
Onlineausarbeitung: Nikolaj Kulvelis

Schwingender Stab:
Abhängigkeit von l: [math]\hat y=45[/math]°

[math]T\over\sqrt{l}[/math](konstant)

[math]T\over\sqrt{l}[/math][math]\approx[/math]1,76 [math]s\over\sqrt{m}[/math]

[math]\Updownarrow[/math]

[math]T=1,76[/math][math]s\over\sqrt{m}[/math][math]sqrt{l}[/math]

[math]T=1,76[/math][math]s\over\sqrt{m}[/math][math]sqrt{2l'}[/math]

[math]T\approx 2,5[/math][math]s\over\sqrt{m}[/math][math]sqrt{l'}[/math]

Fadenpendel:
Abhängigkeit vom l: [math]\hat y=20[/math]°

[math]l\over T^2[/math][math]\approx 24[/math][math]m\over s^2[/math] (konstant)

[math]\Updownarrow[/math]

[math]T=\sqrt{l\over 0,24\frac{m}{s^{2}}[/math][math]=[/math][math]\sqrt{1 s^2\over 0,24 m}[/math][math]\cdot\sqrt{l}[/math]

[math]T\approx 2,0[/math][math]s\over\sqrt{m}[/math][math]\cdot\sqrt{l}[/math]

Fehlerbetrachtung

Bei den obigen Messwerten liegen natürlicherweise gewisse Ungenauigkeiten und Messfehler vor. In diesem speziellen Fall liegt das Fehlerspektrum bei der Periode [math]T[/math] bei ca. 0,05 sek und bei der Fadenlänge [math]l[/math] bei ca. 0,2 cm. Mit diesen Werten lässt sich nun ein Maximal- und ein Minimalwert errechnen. Der Durchschnitt dieser Extremwerte bietet dann eine zuverlässige Lösung für die Konstante [math]a[/math].

Fadenpendel:

[math]T\approx 1,915 \frac{s}{sqrt{m}}\sqrt{l}[/math]

[math]\rightarrow 1,915 \frac{s}{sqrt{m}}\approx\frac{T}{sqrt{l}}[/math]

Max./Min. Betrachtung

[math]\bar T=1{,}32\pm 0{,}05s(\pm3{,}8%)[/math]

[math]l=47{,}5cm\pm0{,}2cm(\pm0{,}4%)[/math]

[math]\Rightarrow\[/math][math]a[/math][math]_m_a_x={(1{,}32+0{,}05)s \over \sqrt{(47{,}5-0{,}2)cm}}=1{,}992{s\over\sqrt{m}}[/math]

[math]a[/math][math]_m_i_n={(1{,}32-0{,}05)s\over\sqrt{(47{,}5+0{,}2)cm}}=1{,}838{s\over\sqrt{m}}[/math]

[math]\Longrightarrow[/math][math]a[/math][math]=1{,}915{s\over\sqrt{m}}\pm0{,}08{s\over\sqrt{m}}(\pm4%)[/math]

Eine statistische Auswertung der Messwerte ist nicht möglich, da jeweils nur drei Zeitmessungen vorgenommen wurden, was zu wenig ist. Vgl mit Messunsicherheit und Fehlerrechnung.

Zusammenfassung

Die experimentelle Untersuchung der Schaukel begann damit, sich Fragen zu der Schaukel zu überlegen, etwa welche Kräfte auf die Schaukel wirken oder von was die Periodendauer T abhängt. Daraufhin wurden direkt vor Ort Experimente und Messungen durchgeführt, um diese Fragen zu beantworten. Als technische Hilfsmittel dienten uns zur Zeitmessung eine Handstoppuhr,und zum Messen der verschiedenen Längen ein Metermaß. Außerdem zogen wir zur genaueren Beschreibung der Bewegung der Schaukel im Raum eine Videoanalyse hinzu.

Es wurde induktiv, d.h. vom Beispiel über Versuche zur allgemeinen Formel, gearbeitet und vorgegangen. Induktives Vorgehen zeichnet sich dadurch aus, dass von Speziellem (eine Messung an der Schaukel) auf Allgemeines (allgemein gültige Formeln) geschlossen wird.

Um Ergebnisse zu bekommen, die nicht nur für unsere Schaukel gelten, haben wir die Situation für ein Experiment vereinfacht. Die Schaukel wurde duch eine Kugel an einem Faden ("Fadenpendel") oder durch eine Stange ersetzt. Durch die Vereinfachung wird die Situation zwar übersichtlicher, entfernt sich aber auch von der realen Schaukel.

Man erhält beim schwingenden Stab und beim Fadenpendel jeweils einen funktionalen Zusammenhang zwischen Länge und Periode. Dieser gilt streng genommen nur für die untersuchte Amplitude. Das heißt, der Proportionalitätsfaktor hängt noch von der Amplitude ab. Ein Vergleich der beiden Schwingungen zeigt, dass der Stab, bei gleicher Länge, eine größere Periode hat. Das liegt am größeren Trägheitsmoment des Stabes, denn der Stab dreht sich beim Schwingen um seinen Schwerpunkt, der Versuch war von der Masse Unabhängig.

Die erzielten Ergebnisse konnten wir an der realen Schaukel überprüfen. Die Abweichungen lagen im Rahmen der Vereinfachungen des Experiments.