Aufgaben zur Überlagerung von Bewegungen / vektorieller Impulsänderung (Lösungen)

Ein Steinwurf

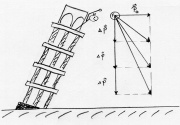
Jemand wirft einen Stein waagrecht von einem 20m hohen Turm.

1. Der Stein ist träge, er behält seinen Impuls und bewegt sich zunächst horizontal weiter. Durch die Gravitation wirkt eine Gewichtskraft nach unten und der Stein erhält nach und nach immer mehr Impuls nach unten.

2. Der Stein hat eine Impulsmenge von [math]p= m\, v = 0{,}5\,\rm kg \cdot 12\,\rm m/s = 6\,\rm Hy[/math] nach rechts.

3. Auf den Stein wirkt eine Kraft der Stärke

[math]F_G=m\,g = 0{,}5\,\rm kg \cdot 10\,\rm N/kg = 50\,\rm N[/math] nach unten.

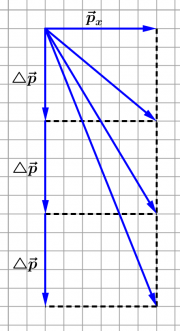
4. Der Stein erhält in jeder Sekunde 50 Huygens nach unten, denn: [math]\triangle \vec p=\vec F\,\triangle t} [/math]

5. Der x-Impuls bleibt konstant bei 50Hy. Der y-Impuls nimmt mit der Zeit zu. Die Menge des Gesamtimpulses kann man mit dem Satz des Pythagoras berechnen:

[math]p_x=6\,\rm Hy[/math]

[math]p_y=50\,\rm N \cdot t[/math]

Zeit  px   py    p
0s    6Hy   0Hy   6Hy
0,1s  6Hy   5Hy   7,8Hy
0,2s  6Hy  10Hy  11,7Hy
0,3s  6Hy  15Hy  16,2Hy

6. In x-Richtung behält der Stein seine Geschwindigkeit bei. In y-Richtung führt er einen freien Fall aus.

Die Ortsgesetze lauten:

[math]s_x=12\,\rm \frac{m}{s} \cdot t \qquad s_y=\frac{1}{2}\cdot \, 10\,\rm \frac{m}{s^2}\cdot t^2[/math]

Die Geschwindigkeitsgesetze lauten:

[math]v_x=12\,\rm \frac{m}{s} \qquad v_y= 10\,\rm \frac{m}{s^2}\cdot t[/math]

Wie lauten die Ortsgesetze s_x(t) und s_y(t), sowei die Geschwindigkeitsgesetze v_x(t) und v_y(t)? 7. Wie lange dauert es, bis der Stein am Boden ankommt? 8. Wie weit wird der Stein geworfen?

Ein Brunnen

Bei einem Brunnen spritzt das Wasser waagrecht heraus und fällt 80cm tief bis auf die Wasseroberfläche. Ein Wasserstrahl (a) kommt dabei 20cm weit ein anderer (b) 40cm.

1. Warum muss die Austrittsgeschwindigkeit des einen (a) nur halb so groß wie diejenige des anderen (b) sein?

Tipp: Welche Zeitdauer fällt ein Wassertropfen vom Austritt bis zur Wasseroberfläche?

Tipp: Wie große sind die Austrittsgeschwindigkeiten?

2. Unter welchem Winkel treffen die Wasserstrahlen auf die Wasseroberfläche?

Tipp: Mit welcher horizontalen und mit welcher vertikalen Geschwindigkeit treffen die Wassertropfen auf die Wasseroberfläche?