Geschwindigkeits- und Beschleunigungsdiagramme von Bewegungen
Inhaltsverzeichnis
Beschreibung einer Bewegung
Wie schnell ist der Gegenstand?
Die Geschwindigkeit ist die zeitliche Änderung des Ortes. ([math]\dot s[/math]) Bei einer eindimensionalen Bewegung wird die Richtung entgegen dem Koordinatensystem mit einem negativen Vorzeichen ausgedrückt. In der Fläche und im Raum ist die Geschwindigkeit eine vektorielle Größe und wird als [math]\vec v[/math] notiert.
Bremst/beschleunigt der Gegenstand?
Die Beschleunigung ist die zeitliche Änderung der Geschwindigkeit. [math]a = \dot v[/math] Im eindimensionalen gibt ein negatives Vorzeichen die Verringerung der Geschwindigkeit, also einen Bremsvorgang an. In der Fläche und im Raum ist sie auch eine vektorielle Größe und wird [math]\vec a[/math] geschrieben.
Beschreibung des zeitlichen Verlaufs
Wann ist der Körper wie schnell?
Ordnet man jedem Zeitpunkt der momentanen Geschwindigkeit zu, so erhält man das Geschwindigkeitsgesetz [math]v(t)[/math]. Das Schaubild heißt Geschwindigkeit-Zeit-Diagramm.
- Die Steigung einer Tangente im Geschwindigkeit-Zeit-Diagramm ist die momentane Beschleunigung [math]a=\dot v[/math],
- die Sekantensteigung ist die mittlere Beschleunigung [math]\bar a= \frac{\Delta v}{\Delta t}[/math]
Flächen in Diagrammen
Die Flächen zwischen dem Schaubild und der Zeitachse lassen sich anschaulich interpretieren. Grundlage dazu ist der sogenannte Hauptsatz der Differential-Integralrechnung (HDI), den man in Worten so formulieren kann:
Das Integral (die Fläche) unterhalb der Änderungsrate ergibt die Gesamtänderung. Dabei werden Flächen unterhalb der x-Achse negativ gewertet.
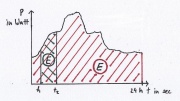
Trägt man z.B. die zeitliche Änderungsrate der Energie (Leistung) über der Zeit auf, so entspricht die Fläche unterhalb des Schaubildes der Gesamtänderung der Energie.
[math]\Delta E = E_2-E_1 = \int_{t_1}^{t_2}\dot E \mathrm{dt}[/math]
Mit Hilfe des GTRs kann man Flächen unter Schaubildern numerisch bestimmen. (Genauere Beschreibung unter Berechnung von Energiemengen.)
Übertragen auf die Beschreibung von Bewegungen bedeutet das:
- Die Fläche unterhalb des Geschwindigkeit-Schaubildes entspricht der Ortsänderung, also der zurückgelegten Strecke.
- Die Fläche unterhalb des Beschleunigungs-Schaubildes entspricht der Geschwindigkeitsänderung.