Impulserhaltung - Actio gleich Reactio - Schwerpunkterhaltung
Inhaltsverzeichnis
Beispiele
Ein Oktopus mit einem seiner Rückstoß-Trichter. Video (ab 2:14)
Video: NPL Water Rockets Challenge 2010 (Starts ab 3:00)
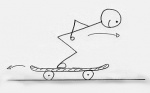
Ein Pendel auf einem Skatebord (Video)
Animation der Luftbewegung an einem Tragflügel
Crashtest Video Fiat 500 und Audi Q7
Abstoßen: Die Bewegung gewinnt Energie
Antriebe: Rakete. Ruderboot. Antrieb durch Propeller /Düsentriebwerk. Vom Skateboard springen. Feder zwischen zwei Wagen. Skateboard Ziehen und Drücken.
Zusammenstoßen: Die Bewegung verliert Energie
Bremsen: Luftwiderstand. Segelboot. Windrad.
Unelastisch: Energie wird in Wärme gewandelt (auf Entropie umgeladen) Skateboard. Wagen auf Fahrbahn mit Knete mit Feder.
Elastisch: Energie wird gespeichert
Schwerpunkt
- Feuerwerk. Pendel auf Skateboard. Laufen oder Rennen mit bewegten Armen Flash Animation (Leistungskurs Sport Rolf Dober)
Impulserhaltung im Wasserbehältermodell
Im Modell hat die Wassermenge zugenommen, weil etwas hineingeschüttet wurd oder abgenommen, weil etwas herausgeflossen ist. Bisher haben wir uns keine Gedanken darüber gemacht, woher das Wasser kommt oder wohin es geht.
Wie beim Wasser ist es auch beim Impuls. Auch der Impuls kommt irgendwoher und geht irgendwohin. Erhält ein Körper Impuls, so verliert ein anderer Gegenstand genau diese Impulsmenge. Verliert ein Gegenstand Impuls, so gewinnt ein anderer Körper diese Impulsmenge.
Vektoriell
- Flugzeugflügel / Vogel. Billiard. Kugel am Wasserstrahl.
Warum fliegt ein Flugzeug?
Wassersportgeräte: Bei google: "wake turbulence"
Links
- Video eines Zusammenpralls zweier unterschiedlich schwerer Fahrzeuge. (youtube: "ADAC Crash Test: Fiat 500 vs. Audi Q7" von "informatiiauto")
- [Re: Crashtest Audi Q7 vs Fiat 500 Video] wie oben (youtube: "Re: Crashtest Audi Q7 vs Fiat 500" von "tottube976")
- Video: Curling Ein Stein stößt gegen zwei andere. (youtube: Jennifer Jones Best Curling Shot! )
- Youtube: JetLev Promo "Jetlev"
- Youtube: Remake of Flyboard by Zapata Flyboard
- Wissen vor acht - Warum fliegen Zugvögel in V-Formation? (youtube.de von "superwissenschaft")
- Animation der Luftbewegung an einem Tragflügel (youtube: "Wing tip vortices behind the wing - Wakesheet" von "jdivahar")
- Landeanflug auf London Schöne Sicht auf den Flügel und die Steuerklappen. (youtube: United 777-200ER Gorgeous Fast Approach and Landing at London Heathrow! von "dantorp11")
Zusammenfassung - Wechselwirkung durch Impulsaustausch
|
"Actio gleich reactio" / Impulserhaltung (3. Newtonsches Axiom) Ändert ein Gegenstand seinen Impuls, so ist immer auch ein Partner beteiligt. Stößt sich der Gegenstand mit der Kraft [math]\vec F[/math] ab, so wirkt die Gegenkraft [math]-\vec F[/math] auf den Partner. Sowohl die Summe der Impulse als auch die Bewegung des gemeinsamen Schwerpunkts bleiben erhalten. |
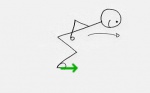
Vereinfachtes Schnittbild des Menschen[1].
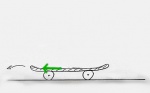
Er wird nach vorne gedrückt.Vereinfachtes Schnittbild des Skateboards mit der Erde[2].
Das Skateboard wird nach hinten gedrückt.
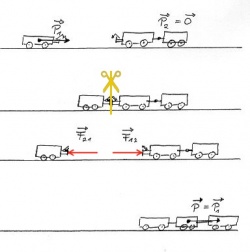
Dies kann man mit drei zeitlichen Phasen beschreiben:
- vorher
- Beide Gegenstände haben zusammen den Impuls [math]\vec p + \vec P[/math]
- Änderung
- Eine Zeit [math]t[/math] lang wirkt auf den Gegenstand eine mittlere Kraft [math]\vec F[/math] und auf den Partner die gleichgroße, aber entgegengesetzt wirkende Gegenkraft [math]-\vec F[/math].
- Der Gegenstand erhält also den Impuls [math]\triangle \vec p = \vec F \cdot t[/math] und der Partner verliert ihn, bzw. bekommt den Impuls [math]-\triangle \vec p[/math][3].
- nachher
- Beide Gegenstände haben ihren Impuls verändert, aber zusammen haben sie immer noch den gleichen Impuls: [math]\vec {p'} + \vec {P'}[/math]
Rechnung
Als Rechenansatz gibt es zwei Möglichkeiten:
- Impulsbilanz
- Man setzt den Impuls vor und nach dem Impulsaustausch gleich:
- [math]p+P = p'+P'[/math]
- Falls die Masse der Gegenstände sich nicht verändert, gilt:
- [math]m \, v + M \, V = m \, v' + M \, V' [/math]
- Nun überlegt man sich, welche Größen gegeben sind und welche Größe nicht. Nach der unbekannten Größe löst man auf.
- Impulsänderung
- Der Impuls ändert sich bei einer zeitlich konstanten Kraft um [math]\Delta \vec p = \vec F \cdot \Delta t[/math].
- Für die Impulse nach dem Kontakt gilt also:
- [math]\vec {p'} = \vec p + \Delta \vec p \quad \text{und} \quad \vec {P'} = \vec P - \Delta \vec p [/math]
- Bei unveränderten Massen folgt daraus:
- [math]m \, \vec {v'} = m \, \vec v + \Delta \vec p \quad \text{und} \quad M \, \vec {V'} = M \, \vec V - \Delta \vec p [/math]
- Teilt man die Gleichungen noch durch die jeweilige Masse, so kann man die Geschwindigkeiten nach dem Impulsaustausch berechnen:
- [math]\vec {v'} = \vec v + \frac{1}{m}\,\Delta \vec p \quad \text{und} \quad \vec {V'} = \vec V - \frac{1}{M}\, \Delta \vec p [/math]
Links
- Flugphysik for Beginners
- Altlasten der Physik: Warum ein Flugzeug fliegt (Friedrich Herrmann)
- ZEIT: Hier irrt die Schulweisheit; Warum kann ein Flugzeug fliegen? Bis heute, kritisieren zwei amerikanische Forscher, wird das falsch erklärt
Referenzfehler: Es sind <ref>-Tags vorhanden, jedoch wurde kein <references />-Tag gefunden.