Das Konzept der Energie (Energieträger und Potential)

(Kursstufe > Theoretisch-deduktives Vorgehen am Beispiel der Energie)

Energie

Money makes the world go round.

Das Glas ist gefüllt mit 0,2l Wasser, doch wieviel Energie steckt in ihm?

• Energie ist das Geld der Physik. Man bewertet damit Situationen.

Es ist alles andere als selbstverständlich, daß wirklich sämtliche Situationen vergleichbar und in einer Einheit auch bewertbar sind.

• Die Energie wird mit einem Energieträger gespeichert. Energie ohne Träger gibt es nicht.
• Energie ist eine Erhaltungsgröße, sie kann weder erzeugt, noch vernichtet werden. (Im Gegensatz zum Geld gibt es auch weder Inflation noch Deflation :)

Die verschiedenen Energieträger sind mit einer Ausnahme auch eine Erhaltungsgröße.

• In der Regel ist die absolute Energiemenge eines Körpers uninteressant. Man interessiert sich viel mehr für die Energiemengen, die hinaus oder hineingehen.
• Die Veränderungen der Energiemenge kann man durch einen Energieträgerstrom beschreiben, der die Energie rein oder raustransportiert.
• Um eine gespeicherte Energiemenge zu bestimmen, muss man den heraus- oder hereinfließenden Energiestrom integrieren.
• Es ist (leider!?) auch üblich der gespeicherten Energie einen anderen Namen zu geben als der Energie, welche strömt. Man nennt die gespeicherte Energie eine Zustandsgröße, die strömende eine Prozessgröße. (In der Chemie wird die Energie häufig als Enthalpie bezeichnet.)

Zustandsgröße	Prozessgröße
mechanische Energie	mechanische Arbeit
thermische Energie	Wärme

Energiemenge eines Wassergefüllten Glases

• Es gibt verschiedene Energieträger (Energieformen):
  • warme Gegenstände: Entropie (thermische Energie)
  • zusammengedrückte oder auseinandergezogene Gegenstände: Feder (Spannenergie)
  • hochgehobene Gegenstände: Schwerefeld (Lageenergie)
  • sich bewegende Gegenstände: Impuls (Bewegungsenergie)
• Bei einigen Energieträgern ist die enthaltene Energiemenge vom Bezugssystem abhängig:
  • Schwerefeld (Lageenergie)
  • Impuls (Bewegungsenergie)

Energie- und Energieträgerströme

Systemisches Denken - Beschreibung eines Zustandes

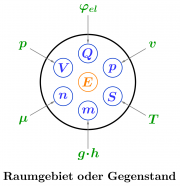
Ein Raumgebiet oder Körper wird einerseits durch die Angabe der enthaltenen Mengen von bestimmten mengenartigen Größen beschrieben.

Weiterhin kann man Eigenschaften durch punktuelle Größen festlegen. Mit Ausnahme der Energie kann jeder extensiven, mengenartigen Größe ist eine punktuelle, intensive Größe zugeordnet werden.

Mengenartige (extensive) Größen	haben zugehörige Eigenschaften (intensive Größen), welche man Potential nennt.
E: Energiemenge [math][E]=\mathrm{J \quad(Joule)}[/math]
S: Entropiemenge [math][S] = \mathrm{Ct \quad (Carnot)}[/math]	ν: absolute Temperatur [math][T] = \mathrm{K \quad (Kelvin)}[/math]
V: Volumen [math][V] = \mathrm{m^3}[/math]	p: Druck [math][p] = \mathrm{Pa \quad (Pascal) = 10^{-5}bar}[/math]
m: Masse [math][m] = \mathrm{kg}[/math]	gh: Schwerepotential [math][gh] = \mathrm{m^2/{s^2} }[/math]
p: Impuls [math][p] = \mathrm{Hy \quad (Huygens)= kg \frac{m}{s}} [/math]	v: Geschwindigkeit [math][v] = \mathrm{m/s} [/math]
Q: el. Ladung [math][Q] = \mathrm{C \quad (Coulomb)}[/math]	φel: el. Potential [math][\varphi_{el}] = \mathrm{V \quad (Volt)}[/math]
n: Stoffmenge [math][n] = \mathrm{mol}[/math]	μ: chem. Potential (freie molare Standardenthalpie) [math][\mu] = \mathrm{J/{mol} \quad (Joule/Mol)}[/math]

Systemveränderungen

Hier vergrößert sich die Energiemenge in den Hühnern entscheidend! .

Auch hier bekommt nicht jedes Huhn die gleiche Energiemenge. (Aus dem Energiebuch des Schroedel Verlags)

• Verändert sich die Energiemenge, so verändert sich auch immer noch eine andere mengenartige Größe, der sogenannte Energieträger!

• Der Energiestrom ist proportional zum Trägerstrom. Das Potential ist gerade die Proportionalitätskonstante.

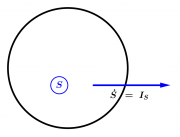
• Eine andere mathematische Schreibweise für die Stromstärke ist die momentane zeitliche Änderungsrate, also die Ableitung nach der Zeit. Die zeitliche Ableitung einer Größe notiert man mit einem Punkt über dem Symbol. Zum Beispiel gilt: [math]I_S = \dot S[/math]

Entropie strömt aus einem Gebiet. Durch den Entropiestrom ändert sich die enthaltene Entropiemenge.

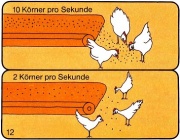
• In der Regel strömt aber Stoff von einem Gebiet in ein Anderes. Sind die Potentiale unterschiedlich, gibt es einen Netto-Energiestrom von den beiden Systemen weg.

Bsp.: Von dem warmen Wasser über das Thermoelement in das kalte Wasser fließt ein Entropiestrom, den man zunächst vereinfachend als konstant ansehen kann. Es kommt weniger Energie an, als wegfließt, weil die Temperatur und damit die Beladung des Entropiestromes abnimmt. Die Energie ist auf die elektrische Ladung umgeladen worden, welche dann wiederum in der Lampe auf das Licht und Entropie geladen wird.

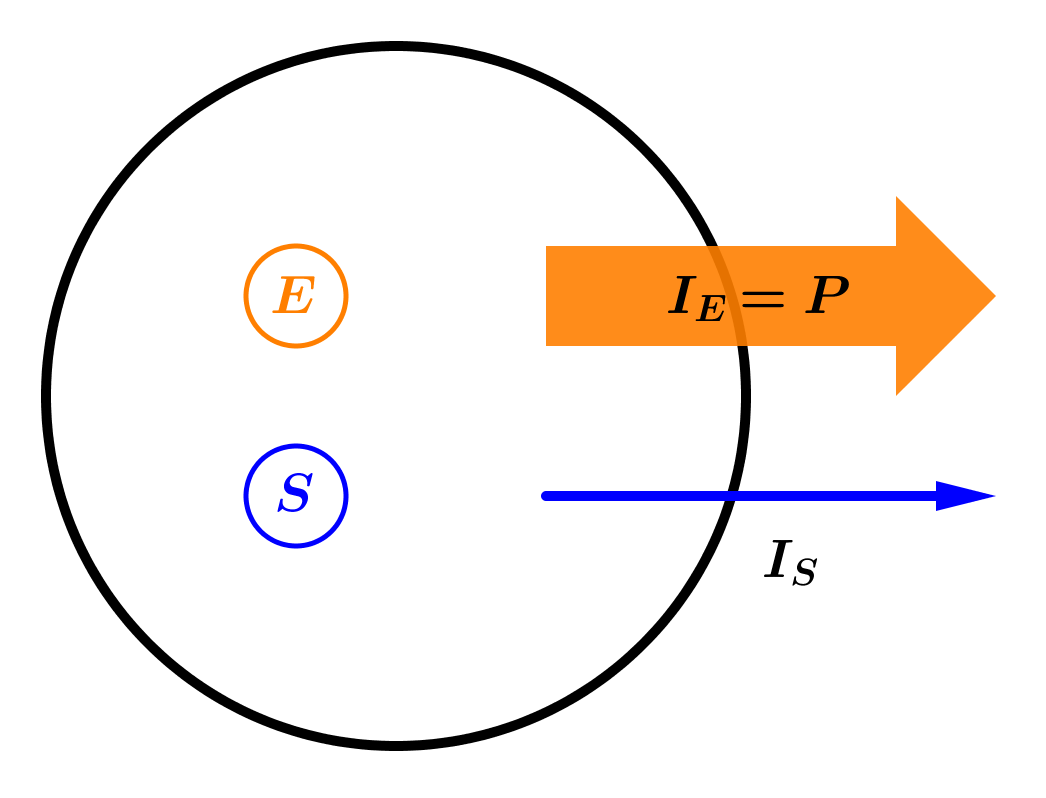
Datei:Energieströme.jpg

P = Energetische Stromstärke/Energiestrom

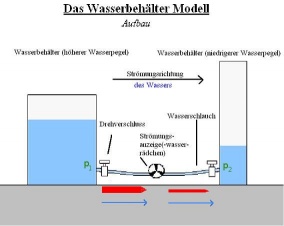
Das Wasserbehältermodell

Das Wasserbehältermodell real

und als Zeichnung.

• Wassermenge und Stromstärke (Durchsatz)
• Wasserhöhe und Druck
• Widerstandskonzept:
  • Druckunterschied als Antrieb
  • Stömungswiderstand
• Energietransportkonzept:
  • Druck als Energiebeladungsmaß
  • Druckunterschied als Potentialdifferenz
  • Energiestromgleichung (Leistung) [math]P=\triangle p I_W \qquad \qquad \dot E = \triangle p \dot W [/math]

Es gibt zwei Konzepte:

1. Antrieb-Widerstand
2. Energieträger & Potenzial

Das Wasserbehältermodell besteht aus zwei, mit unterschiedlich viel Wasser gefüllten, Zylindern. Sobald man die Drehverschlüsse an beiden Seiten aufgedreht, strömt das Wasser aus dem höher mit Wasser gefüllten Bottich in den Zweiten. Dieser Vorgang lässt sich mit Hilfe des Wasserrädchens beobachten und stoppt erst, nachdem die Wasserpegel beider Seiten sich auf ein gleiches Niveau begeben haben.

a) Die Strömung entsteht durch den vonstatten gehenden Druckausgleich, der durch die unterschiedlichen Druckverhältnisse in den Gefäßen verursacht wird. Die Druckdifferenz zwischen dem Zylinder mit dem höheren und dem niedrigeren Wasserpegel, ist der Antrieb. Ein Widerstand besteht durch die Reibung in der Wasserleitung und dem Wasserrädchen, dadurch fließt das Wasser nur langsam in den anderen Behälter.

b) Das Wasser ist der sogenannte Energieträger, der auf der Seite mit dem höheren Wasserpegel, auf Grund des höheren Drucks mit mehr Energie beladen ist. Sobald eine Verbindung zwischen den beiden Behältern gegeben ist, versuchen die unterschiedlichen Energiepegel (Potenziale) sich auf beiden Seiten auszugleichen. Ein Teil der Druckenergie wird „auf dem Weg“ zur anderen Seite zu Wärme umgewandelt, da die Reibung die sogenannte Reibungsenergie freisetzt.

Anwendungen des Wasserbehältermodells in Beispielen

• Luftballon

Ein Luftballon, aus dem Luft entweicht

Trägergröße: Volumen

Potenzial: Druck

[math]I_E=I_v*p \qquad[/math] oder: [math]\dot E= \dot V*p[/math]

[math]E= V \, \bar p[/math]

Wenn beim Druck [math]p[/math] der Luftballon um das Volumen [math]V[/math] kleiner wird, so verringert sich die enthaltene Energie um [math]\triangle E = V*p[/math]

In der Regel wird sich aber der Druck im Ballon ändern,weshalb man zur Bestimmung der gesamten Enrgiemenge integrieren muss oder den mittleren Druck [math]\bar p[/math] verwenden muss.

• Schokolade

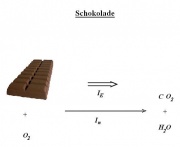
Schokolade

T: Stoffmenge

φ: chem. Potenzial μ

[math]I_E=I_n*\mu[/math] oder: [math]\dot E=\dot n*\mu[/math]

[math]E=n*\mu[/math]

Bei der Änderung der Schokoladenstoffmenge ändert sich das chemische Potenzial nicht. Deswegen gilt hier: [math]E=n*\mu[/math]

• Kochplatte

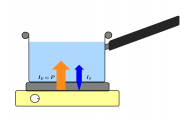
Kochplatte & Topf mit Wasser

Träger: Entropie S

Potenzial: Temperatur [math]T[/math]

[math]I_E=I_S*T[/math] oder: [math]\dot E=\dot S*T[/math]

Um die in einem "warmen" Gegenstand enthaltene Energiemenge zu bestimmen, könnte man sich vorstellen, dass man ihn vom absoluten Temperaturnullpunkt an erwärmt. Während des Erwärmens fließt ständig Entropie und damit auch Energie hinein. Da die Temperatur sich dabei verändert, müßte man einen genauen Entropieverlauf in Abhängigkeit der Temperatur kennen.

Einfacher ist der Fall, dass sich die Temperaturen von Herdplatte und Topf nach einer längeren Zeit konstant bleiben. Für diesen Fall gilt wieder, dass pro Sekunde die Energiemenge [math]E= S*T [/math] in den Topf fließt.

Da jedoch die Temperaturen von Kochplatte und dem Topf (bzw. dem Wasser) unterschiedlich sind stoßen wir auf eine Besonderheit:

da vorausgesetzt ist dass der Energiestrom konstant ist d.h. dass keine Energieverluste auftreten, dass System jedoch eine Temperaturdifferenz aufweist muss, um der Forderung gerecht zu werden Entropie erzeugt werden.

D.h. durch das fliessen der Entropie wird "neue" Entropie erzeugt.

Temperatur der Kochplatte: [math]T_1[/math]

Temperatur des Topfes: [math]T_2[/math]

Mit [math]I_E=I_S*T[/math] folgt

für den Entropiestrom aus der Platte: [math]I_{S_1} = \frac{I_E}{T_1} [/math]

für den Entropiestrom in den Topf: [math]I_{S_2} = \frac{I_E}{T_2} [/math],

wobei [math]I_{S_1} \lt I_{S_2}[/math]!

• Stausee

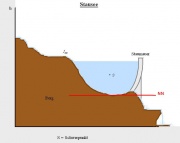
Stausee

T: Schwerefeld, "m"

[math]\varphi[/math]: gh

[math]\dot E=\dot m * gh[/math]

[math]E=m*g \bar h[/math]

Fließt der Massestrom auf einer konstanten Höhe in den See, so fügt jede Masse m dem See die Energie m*gh zu.

Die Energie des gesamten Stausees beträgt: [math]E=m*gh_S[/math]

• Ein Wagen rollt aus

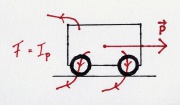
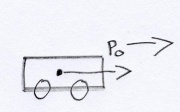
Ein Wagen rollt aus

Träger: Impuls [math]p[/math]

Potenzial: Geschwindigkeit [math]v[/math]

[math]\dot E=\dot p\, v [/math] oder: [math]P=F\, v[/math]

[math]E=p\, \bar v = \frac{1}{2}p\,v =\frac{1}{2}m\,v^2[/math]

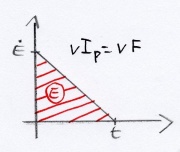
In diesem Fall ändert sich das Potenzial während des Vorgangs. Es ist nicht korrekt zu sagen, dass der Wagen die Energiemenge [math]E=pv[/math] enthält.

Nimmt man den einfachen Fall an, dass eine konstante Kraft einen Gegenstand auf eine bestimmte Geschwindigkeit beschleunigt, so nimmt die Geschwindigkeit gleichmäßig zu und die mittlere Geschwindigkeit ist daher die Hälfte der maximalen.

Oder man bestimmt die Fläche im p-v-Diagramm.

Demnach beträgt die Energie eines Gegenstandes mit dem Impuls p und der Geschwindigkeit v:

[math]E=\frac{1}{2}p\,v = \frac{1}{2}m\, v^2[/math]

Für diesen besonderen Fall kann man die Energiestromstärke auch anders berechnen.

a)[math]v=\dot s[/math] (Die Geschwindigkeit ist die zeitliche Ableitung des Ortes)

b)[math]\dot E=F\dot s[/math]

c)[math]E=Fs[/math] (Kraft [math]F[/math] ist konstant!)

Wenn der Wagen auf einer Strecke von 2m ausrollt und von der konstanten Kraft der Stärke 3N gebremst wird, so waren ursprünglich [math]E=3N*2m=6Nm=6[/math]Joule im Wagen.

Berechnung von Energiemengen

Energiemonitor

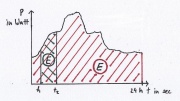
Das Integral der Änderungsrate ergibt die Gesamtänderung.

Trägt man z.B. die zeitliche Änderungsrate der Energie (Leistung) über der Zeit auf, so entspricht die Fläche unterhalb des Schaubildes der Gesamtänderung der Energie.

[math]\triangle E=E_2-E_1=\int_{t_1}^{t_2} \dot E\, dt[/math]

Mit Hilfe des GTRs kann man Flächen unter Schaubildern numerisch bestimmen.

Für den TI-83 gibt man zunächst die Funktion f(x)im Funktionenfenster (Y=) ein. Danach muss man die Fenstergröße so einstellen, dass der gewünschte Bereich sichtbar ist (WINDOW oder ZOOM). Dann kann man das Integral berechnen. Man wählt den Befehl CALC -> 7:Sf(x)dx und gibt die Grenzen lower und upper limit an, am einfachsten, indem man sie eintippt.

Anwendungsaufgaben

Luftballon

Energiestromstärke des Ballons

[math]V=2l[/math] [math]p=10^5 Pa[/math]

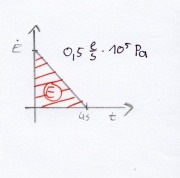
Annahme: Der Druck nimmt linear ab, Luft fließt zum Druck p=0 Pa mit konstanter Änderung [math]\dot V = 0,5 l/s[/math]

[math] E = 0,5*4s*0,5l/s*10^5 Pa[/math]

[math] E = 1*10^2J [/math]

rollender Wagen

p=4Hy v=3 m/s

Lösung:

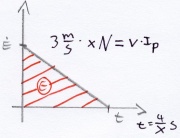
Annahme:F ist konstant F=xN

[math]E=1/2(3m/s)xN*4/x s =6Nm =6J[/math]

• Allgemein

Annahme: F ist konstant

p/F [F=p/t]

[math]E=1/2*p/F*vF[/math]

[math]E=1/2pv[/math]

[math]E=1/2mv^2[/math] !

Energie eines Luftballons

[math]E=I_V*p[/math]

[math]E=V/F*p[/math]

[math]E=1/2t*V/t*p[/math]

[math]E=1/2V*p[/math]

Energie einer elektrisch geladenen Kugel

Die Kugel enthalt die Ladungsmenge Q auf dem Potential [math]\varphi_{el}[/math]. Man nimmt vereinfachend an, dass sie mit einem konstanten Entladungsstrom [math]I = Q/t[/math] entladen wird und, dass das Potential linear abnimmt.

[math]\dot E= \dot Q \, \varphi_{el} = I \, \varphi_{el}[/math]

[math]E=1/2 \, I \, \varphi_{el} \, t = 1/2 \, Q/t \, \varphi_{el} t [/math]

[math]E=1/2 \, Q \, \varphi_{el}[/math]

Energiebedarf einer Ölheizung

Ein Haus, das mit eiener Ölheizung auf eine Temp. von 25°C geheizt wird, hat einen Wärmeverlust von 30Ct/s.

Wie groß ist der Energieverbrauch der Heizung?

Berechnung:

25°C=298,2K

[math]I_E=I_S*T[/math]

=298,2K * 30Ct/s

=8946W

Energiebedarf einer Wärmepumpe

Ein Schwimmbad wird mit einer Wärmepumpe geheizt. Die Wärmepumpe nimmt die Entropie aus einem vorbeifließendem Bach.

Die Temp. des Wassers im Bach ist 19°C, die des Wassers im Schwimmbad 23°C. Das Wasser im Scheimmbad verliert ständig Entropie an die Umgebung, und zwar pro Sekunde 503Ct. Damit es seine Temp. behält muss, muss die Wärmepumpe diese Entropie ständig nachliefern.

Wie hoch ist der Energieverbrauch dr Wärmepumpe?

Berechnung:

Da die Wärmrpumpe die Temp. des Wassers nur von 19°C auf 23°C "anheben" muss, müssen wir als Potenzial der Entropie die Temperaturdifferenz, d.h. 4°C , betrachten:

296,2K-292,2K=4K

[math]I_E=I_S*T[/math]

=4K * 503Ct/s

=2012W

Entropiefluß einer Kochplatte

Der Heizdraht einer 1010-w-Kochplatte hat eine Temp. von 1100K

(a)

Wie viel Entropie wird pro Sekunde im Heitzdraht erzeugt?

(b)

Auf der Kochplatte steht ein Topf mit Wasser; Die Wassertemp. beträgt 370K. Wieviel Entropie kommt pro Sekunde im Wasser an?

(c)

wieviel Entropie wird auf dem Weg vom Heitzdraht zum Wasser erzeugt?

Berechnung:

(a)

[math]I_E=I_S*T[/math]

=>[math]I_S=I_E/T[/math]

=1010W/1100K

=0.918Ct/s

(b)

Da durch den Entropiestrom Entropie erzeugt wird tritt die Besonderheit auf dass, da die Temp. niedriger im Wasser als auf der Kochplatte ist, der Entropiestrom im Wasser größer seien muss.(Vgl. Kochplatte)

[math]I_S=I_E/T[/math]

=1010W/370K

=2.729Ct/s

(c)

[math]I_S(a)-I_S(b)=I_S(c)[/math]

=2,729ct/s-0.918Ct/s

=1.811Ct/s

Praktikum: Bestimmung von Energie- und Entropiekapazität von Wasser und Wasserdampf

Aufbau:

Der Versuchsaufbau

Materialien:

1. 1 Behälter(Plastikeimer ca. 1 Liter, Stiroporbecher ca. 1/2 Liter, etc.)

2. 1 Tauchsieder (ca.230W/ca.1000W)

3. Bestimmte Menge Wasser

4. Stoppuhr

5. Waage

6. Leistungsmesser

Zu messsen:

Das Ziel ist es herauszufinden wieviel Energie man bei gegebenem Druck benötigt, um eine best. Menge an Wasser um belebieg viele Grad kelvin zu erwärmen.

Einfachheitshalber stellen wir uns expliziet die Farge, wie viel Energie benötigt wird um 1Kg wasser um 1K zu erwärmen.

Dazu benötigen wir nun die Menge Wasser (muss nicht unbedingt 1Kg sein), welche mit dem Tauchsieder auf eine bestimmte Temperatur angehoben wird.

Essentiel bei dieser Fragestellung ist natürlich noch die Leistung des Tauchsieders, welche mittels eines Leistungsmessers bestimmt wird. Dieser funktioniert im Prinziep wie ein Amperemeter.

jetzt muss nur noch die Zeit "festgehalten" werden die gebraucht wird um das Wasser um eine bestimmpe Anzahl von Kelvin zu erwärmen.

Beobachtung:

Theta/J.

Die Temperatur nimmt mit der Zeit gleichmäßig zu. Deshalb nimmt auch die Energiemenge gleichmäßig zu!

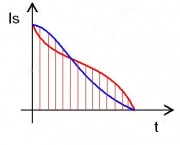
Die Entropieströmung [math]I_S = I_E / T[/math] nimmt mit der Zeit ab, weil der Energiestrom konstant bleibt.

Erklärung

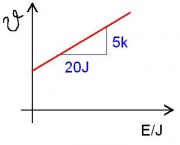
(1)Die Wärmekapazität von Wasser (siehe Bild) [math]\dot S=I_S[/math] Energie in 20s: [math]E=20S*288W=5760J[/math]

                              Energie pro K: 1152J
                              Für 1 Kg: 3879J

Die Wärmekapazität von Wasser ist also ca. [math]3,9KJ/Kg K[/math] -->Man benötigt um Wasser zu erwärmen 3,9 KJ pro Kilogramm und pro Kelvin

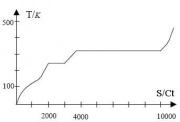
(2)Bestimmung der hineingeflossenen Entropie [math]I_E=T*I_S[/math] -->[math]Is=\dot S=I_E/T[/math]

I_S/t.

Die hineingeflossene Entropiemenge ergibt sich als Fläche im Diagramm. Offensichtlich benötigt man zu Beginn der Erwärmung mehr Entropie als am Ende.

Da die Abnahme des Entropiestrom annähernd linear verläuft, kann man ohne großen Fehler die mittlere Entropiestromstärke aus der mittleren Temperatur [math]\bar T[/math] berechnen: [math]\bar I_S \approx P/{\bar T}[/math]. Man erhält dann für die Zunahme der Entropie:

[math]S = \bar I_S \quad t = E / \bar T[/math]

Die Entropiezunahme ist also ungefähr gleich der Energiemenge dividiert durch mittlere Temperatur.

Der Zusammenhang von Entropiegehalt und Temperatur bei 1kg Wasser.