Eigenschwingungen von ausgedehnten Gegenständen ("Stehende Wellen")

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche

(Kursstufe > Mechanische Wellen)

Beispiele

  • schwingende Platten (Chladnische Figuren)
  • Schwingende Stäbe:
    • Xylophon, Metallophon, Klangstab, Alurohr eines Windspiels
  • Gittarre, Geige, ...
  • Flaschen anblasen:
    • Überblasen
    • Wasser einfüllen
    • Bei zwei verschieden großen Flaschen die gleiche Tonhöhe einstellen (Wovon hängt die Tonhöhe ab: Luftvolumen, Höhe der Luftsäule, Material der Flasche, ...)
  • Flöte: Tonleiter spielen, Überblasen, untere Öffnung zuhalten
  • Orgelpfeife: Länge der Pfeide variieren, offenes Ende zuhalten
  • "Heulrohr"

Schwingungen sichtbar machen

Versuch: Kundtsches Rohr

Aufbau

a) Vor ein an beiden Seiten offenes Glasrohr wird ein Lautsprecher gestellt, der mit einem Frequenzgenerator verbunden ist. In dem Rohr befindet sich feines Korkmehl, das man gut mit einer längeren Winkelleiste hineinbekommt. Ausgehend von einer eher niedrigen Frequenz (50 Hz) wird die Höhe des Tons immer weiter vergrößert.

b) Auf die eine Seite des Rohrs wird ein Gummistopfen gemacht und der Versuch wiederholt.

Versuchsaufbau Kundt Röhre 0.jpg
Versuchsaufbau Kundt Röhre Detail.jpg
Alternativer Aufbau

Beobachtung

  • Ohne Ton

  • Die Grundschwingung

  • Zwei Geschwindigkeitsbäuche

  • Mir rätselhafte Linien innerhalb eines Geschwindigkeitsbauches

a) Das Korkmehl wird bei bestimmten Frequenzen aufgewirbelt und bildet Muster:

Bei 220 Hz:
Bei Hz:

b) Ist ein Ende geschlossen, verändern sich die Muster und Frequenzen:

Bei 110 Hz:
Bei 220 Hz:

Animation

Versuch: Schwingendes Wasser in einer Wanne

Handversuch: Eigenschwingungen einer Spiralfeder

Versuch: Schwingende Platte (Chladni-Figuren)

Schwingung Lernzirkel Cladni.jpg

Aufbau

Auf eine Metallplatte wird Sand gestreut. Dann schlägt man sie mit einem Klöppel an verschiedenen Stellen an. (Man kann sie auch mit einem Geigenbogen anstreichen. So hat Ernst Florens Friedrich Chladni das im 18. Jh. gemacht)

Mit einem Vibrationsgenerator (Lautsprecher mit aufgesetztem Stift) kann man die Platte an verschiedenen Stellen mit einer vorgegebenen Frequenz anregen.

(Der Versuch ist auch Teil des Lernzirkels zu Schwingungen.)


Beobachtungen

  • Chladnische Figuren mit Sand pdf oder html (Uni Ulm, Vorlesungssammlung Physik Online Archiv, mit Versuchsaufbau)

Animationen

In diesen Animationen kann man die Eigenschwingungen einer rechteckigen / kreisrunden Platte sehen. Wird ein Feld grün markiert, so wird eine Eigenschwingung gezeigt. Bei mehreren Markierungen werden die Eigenschwingungen überlagert.

Erklärung durch Überlagerung von Wellen als "Stehende Welle"

Zwei Wellenzüge gleicher Wellenlänge und Amplitude überlagern sich.
Die stehende Welle zwischen zwei Quellen in 2D.
und in 3D (Standbilder der Wellenwanne von Paul Falstad.)

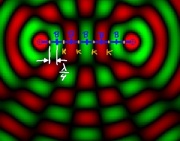
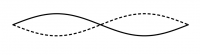
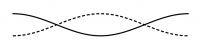
Überlagern sich zwei gegenläufige Wellen mit gleicher Wellenlänge und gleicher Amplitude, so ergibt sich in regelmäßigen Abständen von einem Viertel der Wellenlänge konstruktive und destruktive Interferenz. Dieses Phänomen hat man auch bei der Zwei-Quellen-Interferenz in dem Gebiet zwischen zwei Lautsprechern beobachten können. Die Überlagerung sieht aus wie eine "Stehende Welle" und heißt deswegen auch so. Die Stellen mit konstruktiver Interferenz heißen Bäuche, die mit destruktiver Interferenz Knoten. (Animation)

Stehende Wellen sind aber keine Wellen mehr, sondern eine Schwingung durch die Formveränderung eines Körpers. Denn bei einer stehenden Welle wird überhaupt keine Energie oder Impuls transportiert. Beide Wellen haben die gleiche Intensität, aber in gegenläufigen Richtungen.

Man kann die Eigenschwingungen von ausgedehnten Körpern aber sehr schön mit Hilfe von Wellen beschreiben. An den Rändern des schwingenden Gegenstandes wird die Welle reflektiert. Je nach Art des Randes aber unterschiedlich, was man in diesem Video sehen kann. An einem offenen (losen) Ende wird ein Wellenberg als Wellenberg reflektiert. An einem geschlossenen (festen) Ende als Tal. Man kann auch sagen, dass die Welle bei einem festen Ende einen Phasensprung von [math]\pi[/math] macht.

Überlagert sich die einlaufende Welle mit der reflektierten, so entsteht eine stehende Welle. Das ist in dieser Animation nachzuvollziehen.


  • [math].\quad \lambda_0= \frac{4}{2} \, l \qquad f_0=\frac{2}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_0= \frac{4}{2} \, l \qquad f_0=\frac{2}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_0= \frac{4}{1} \, l \qquad f_0=\frac{1}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_1= \frac{4}{4} \, l \qquad f_1=\frac{4}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_1= \frac{4}{4} \, l \qquad f_1=\frac{4}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_1= \frac{4}{3} \, l \qquad f_1=\frac{3}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_2= \frac{4}{6} \, l \qquad f_2=\frac{6}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_2= \frac{4}{6} \, l \qquad f_2=\frac{6}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_2= \frac{4}{5} \, l \qquad f_2=\frac{5}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_3= \frac{4}{8} \, l \qquad f_3=\frac{8}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_3= \frac{4}{8} \, l \qquad f_3=\frac{8}{4}\, \frac{c}{l} [/math]

  • [math].\quad \lambda_3= \frac{4}{7} \, l \qquad f_3=\frac{7}{4}\, \frac{c}{l} [/math]


Die Eigenfrequenzen unterscheiden sich also je nachdem, ob beide Randbedingungen gleich (offen-offen und geschlossen-geschlossen) oder unterschiedlich sind.

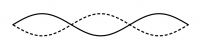
Bei symmetrischen Randbedingen sind alle Vielfache der Grundfrequenz Eigenfrequenzen.

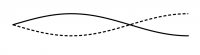
[math] f_n=\frac{2 \,(n+1)}{4}\, \frac{c}{l} \qquad f_n=(n+1)\, f_0 [/math]

Bei unsymmetrischen Randbedingen sind nur ungeradzahlige Vielfache der Grundfrequenz Eigenfrequenzen.

[math] f_n=\frac{2 \,(n+1)-1}{4}\, \frac{c}{l} \qquad f_n=(2\,(n+1)-1)\, f_0 [/math]


Links

Allgemein

Selbsterregte Schwingungen

Chladnische Figuren

Musikinstrumente

Orgeln

Klarinette

Von „http://schulphysikwiki.de/index.php?title=Eigenschwingungen_von_ausgedehnten_Gegenständen_(%22Stehende_Wellen%22)&oldid=9160“