Praktikum: "Wärme": Messung von Entropie- und Energiemengen bei Wasser
Inhaltsverzeichnis
Praktikum: Der Energie- und Entropiefluß eines Mini-Kraftwerks
Aufbau
Bild und Messauftrag
Interpretation
Weg der Energie? Weg der Wärme? Unterscheidung von Energie/Entropie
Praktikum: Bestimmung von Energie- und Entropiekapazität von Wasser und Wasserdampf
Aufbau:
- Materialien:
- 1. Behälter(Plastikeimer ca. 1 Liter, Styroporbecher ca. 1/2 Liter, etc.)
- 2. 1 Tauchsieder (ca.230W/ca.1000W)
- 3. Bestimmte Menge Wasser
- 4. Stoppuhr
- 5. Waage
- 6. Leistungsmesser
- 7. Thermometer
Zu messsen: Das Ziel ist es, herauszufinden wieviel Entropie und Energie sich in Wasser und Wasserdampf befindet.
Dazu erhitzt man eine gewisse Menge Wasser mit einem Tauchsieder und läßt es dann eine Weile kochen. Durch Messung der Leistung des Tauchsieders bestimmt man die zugeführte Energiermenge. Während des Erwärmens wird ständig die Temperatur und die verstrichene Zeit gemessen und danach auch die Menge des verdampften Wassers bestimmt.
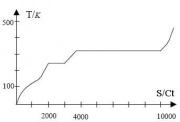
- Erstellen Sie zunächst ein Diagramm des zeitlichen Temperaturverlaufs T(t). (T ist die absolute Temperatur in Kelvin.) Wie interpretieren Sie den Verlauf?
- Bestimmen Sie die die Wärmeenergiekapazität und die Verdampfungsenergie von Wasser. (In der Chemie spricht man von Verdampfungsenthalpie oder der latenten Wärme.)
- Können Sie auch angeben, wieviel Entropie man benötigt, um ein Kilogramm Wasser zu verdampfen?
- Wieviel Entropie benötigt man bei der Erwärmung des Wassers?
Beobachtung:
Die Temperatur nimmt mit der Zeit gleichmäßig zu. Deshalb nimmt auch die Energiemenge gleichmäßig zu!
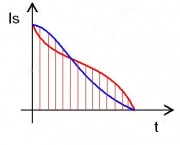
Die Entropieströmung [math]I_S = I_E / T[/math] nimmt mit der Zeit ab, weil der Energiestrom konstant bleibt.
Erklärung
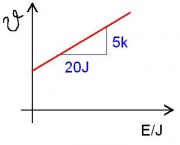
(1) Die Wärmekapazität von Wasser (siehe Bild) [math]\dot S=I_S[/math] Energie in 20s: [math]E=288\,\rm W \cdot 20\, s = 5760\,\rm J[/math]
Energie pro K: 1152J
Für 1 Kg: 3879J
Die Wärmekapazität von Wasser ist also ca. [math]3,9KJ/Kg K[/math] -->Man benötigt um Wasser zu erwärmen 3,9 KJ pro Kilogramm und pro Kelvin
(2)Bestimmung der hineingeflossenen Entropie [math]I_E=T*I_S[/math] -->[math]Is=\dot S=I_E/T[/math]
Die hineingeflossene Entropiemenge ergibt sich als Fläche im Diagramm. Offensichtlich benötigt man zu Beginn der Erwärmung mehr Entropie als am Ende.
Da die Abnahme des Entropiestrom annähernd linear verläuft, kann man ohne großen Fehler die mittlere Entropiestromstärke aus der mittleren Temperatur [math]\bar T[/math] berechnen: [math]\bar I_S \approx P/{\bar T}[/math]. Man erhält dann für die Zunahme der Entropie:
[math]S = \bar I_S \quad t = E / \bar T[/math]
Die Entropiezunahme ist also ungefähr gleich der Energiemenge dividiert durch mittlere Temperatur.
Links
- Kleines Script zur Entropiemessung (Michael Pohlig)