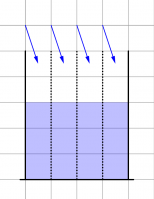
Senkrechte Fallbewegungen auf der Erde mit und ohne Reibung
Inhaltsverzeichnis
Beispiele
Eine Feder fällt langsamer zu Boden als ein Stein! Wirklich immer? ...auf dem Mond ...in einer Vakuumkammer
Versuche
Ein großer und ein kleiner Stein fallen
- Vorüberlegungen
Der große Stein hat eine größere Gewichtskraft als der kleine, deshalb fällt er schneller zu Boden.
Vielleicht spielt die Dichte der Steine eine Rolle.
- Aufbau
Die beiden Steine auf "Drei" auf eine Pappunterlage fallenlassen.
- Beobachtung
Sie kommen beide gleichzeitig unten an!
- Erklärung durch einen Gedankenversuch
- Annahme: Der große Stein fällt schneller als der kleine.
- Dann bindet man beide Steine mit einer Schnur fest zusammen. Wie würden sie nun gemainsam fallen?
- Einerseits bremst der kleine Stein den großen Stein, weswegen sie zusammen langsamer als der große.
- Andererseits bilden beide zusammen einen noch größeren Stein und fallen deshalb schneller als der große Stein!?
- Die Überlegungen führen auf einen Widerspruch! Deshalb ist die Annahme falsch. Beide Steine fallen also in gleicher Art und Weise zu Boden!
- Erklärung durch Zerteilung
- Teilt man einen Stein in einige kleinere Teile (z.B. indem er hinfällt:), so kann man ihn wieder zu einem Stein zusammensetzen.
- Fallen nun die zusammengesetzten Teile anders als der ganze Stein? Es ist nicht einzusehen, warum sich die fallenden Einzelteile gegenseitig beeinflussen sollten. Alle fallen für sich genauso wie der ganze Stein zusammen.
- Erklärung durch Trägheit und Schwere
- Ein größerer Stein hat durch seine größere Masse eine größere Schwere und damit eine größere Gewichtskraft. Aber andererseits hat er auch eine größere Trägheit. Bei einer großen Kraft verändert sich der Impuls schnell aber bei einer großen Trägheit verändert sich der Impuls nur langsam! Beide Effekte scheinen sich genau aufzuheben.
Eine Feder und ein Stein fallen
- Aufbau
Einfach Feder und Stein fallen lassen.
- Beobachtung
Die Feder fällt ganz langsam zu Boden, der Stein ist viel schneller am Boden.
- Erklärung
Warum fällt die Feder so langsam? An ihrer kleinen Masse kann es nicht liegen, denn ein Stein der gleichen Masse müßte, wie man schon gesehen hat, genauso wie der große Stein fallen.
Der Unterschied zwischen der Feder und einem Stein gleicher Masse ist offensichtlich, dass die Feder "viel mehr im Raum verteilt ist". Dadurch hat sie viel mehr Kontaktfläche zur Luft. Wahrscheinlich ist die Wechselwirkung zwischen Der Feder und der Luft viel größer als bei einem Stein.
Eine Feder und ein Stein fallen im luftleeren Raum
- Aufbau
Eine Feder fällt in einer Flasche
- Aufbau
Ein Blatt Papier fällt
- Aufbau
a) Ein Blatt Papier und einen Stein gleichzeitig fallen lassen.
b) Das Papier zerknüllen und nochmal beide fallenlassen.
Die Bewegungsgesetze des freien Falls
Wenn der Luftwiderstand, so wie auf dem Mond, nicht vorhanden ist oder keine große Rolle spielt, spricht man vom "freien Fall".
Wie bewegt sich also ein Stein, den man losläßt? Man weiß, dass nur eine Kraft auf ihn wirkt, die Gewichtskraft. Am Anfang der Bewegung ruht der Stein, er hat noch keinen Impuls. Durch die konstante Kraft bekommt er gleichmäßig immer mehr Impuls. Es ist also eine gleichmäßig beschleunigte Bewegung.
Die Gewichtskraft gibt an, wie schnell sich der Impuls mit der Zeit ändert. Wir nehmen an, dass der Gegenstand am Anfang noch keinen Impuls hat.
- [math]p = F_G\cdot t = m\, g \cdot t \quad \text{, mit } g \approx 10\rm\frac{N}{kg} [/math]
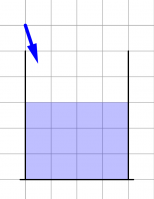
Bei einem Stein mit 400 Gramm Masse, der die Gewichtskraft von 4 Newton hat, wird der Impuls also um 4 Huygens pro Sekunde zunehmen. Wie verändert sich die Geschwindigkeit des Steins? Im Wasserbehältermodell sieht das so aus:
|
[math]s=\frac{1}{2}g\,t^2[/math] | |
|
[math]v= g\,t[/math] |
[math]p = mg\,t[/math] |
|
[math]a = \frac{m\,g}{m} = g[/math] |
[math]F=F_G=m\,g[/math] |
Mit welcher Beschleunigung wird die Geschwindigkeit zunehmen? Ausgehend von der Gewichtskraft erhält man die Bewegungsgesetze:
Die Gewichtskraft berechnet sich als Masse mal Ortsfaktor. Die Beschleunigung ergiebt sich aus der Gewichtskraft, indem man durch die Masse teilt.
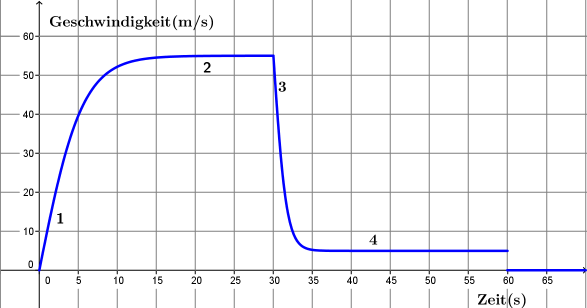
Animation: Fall mit Luftwiderstand im Wasserbehältermodell
Eine Wasserpumpe pumpt Wasser in einen Behälter, der einen Abfluß hat.
Mit den Schiebereglern unter dem Behälter kann man die Bedingungen verändern. Der linke steuert die Zuflussrate, der rechte durch die Größe des Abflußrohres, die Abflussrate. In der Mitte kann man die Behältergröße einstellen.
- Warum steigt die Wassermenge nicht beliebig an, sondern erreicht eine obere Grenze?
- Vergleiche den Fall eines Fallschirmspringers mit dem Füllen des Behälters. Was entspricht dem Wasser, der Zuflussrate, der Abflussrate, der Wasserhöhe?
- Bei einem Fallschirmsprung gibt es zunächst die Freifallphase ohne Schirm. Nach einer gewissen Zeit wird dann der Schirm geöffnet.
- Stelle diesen Vorgang im Modell dar. Wieviel Wasser ist zu Beginn im Behälter? Wie muss man den Zufluss und den Abfluss regeln?
Praktikum: Luftwiderstand eines Papiertrichters
- Material
- Papiertrichter (mit Klebestift aus der Bastelvorlage)
- Handstoppuhr
- Waage
- Ein Maßband (für alle Gruppen)
- Auftrag
Das Ziel ist es den Luftwiderstand eines Papiertrichters bei verschiedenen Geschwindigkeiten zu messen.
Dazu läßt man den Trichter im Treppenhaus fallen und bestimmt seine Endgeschwindigkeit. Diese erreicht der Trichter nicht sofort, deshalb muss man den Trichter erst eine kurze Zeit fallen lassen, bevor man mit der Messung der Strecke und der Zeit beginnt!
Steckt man zwei oder mehrere Trichter ineinander, so erreichen sie eine höhere Endgeschwindigkeit, sie "fallen schneller".
a) Erkläre, warum mehrere ineinandergesteckte Trichter schneller fallen als einer alleine.
b) Messt nun die Masse [math]m[/math] der Trichter und ihre Endgeschwindigkeiten [math]v[/math]. Berechnet die Gewichtskraft [math]F_G[/math] und tragt dann den Luftwiderstand (in N) über die Geschwindigkeit (in m/s) in einem Koordinatensystem auf.
c) Berechnet den Quotienten aus Widerstandskraft und Geschwindigkeit ins Quadrat und tragt die Ergebnisse in die Tabelle ein. Was stellt ihr fest und was kann man daraus schließen?
[math]m \ (\rm in\, g)[/math] [math]F_G \ (\rm in\, N)[/math] [math]\Delta s \ (\rm in\, m)[/math] [math]\Delta t \ (\rm in\, s)[/math] [math]v\ (\rm in \ \frac{m}{s})[/math] [math]\frac{F}{v^2}\ (\rm in \ N \frac{s^2}{m^2})[/math] 1 Kegel
2 Kegel
3 Kegel
4 Kegel
6 Kegel
8 Kegel
Zeugs
- Freier Fall im Windkanal (focus.de)
- Video: Felix Baumgartner - Weltrekord-Sprung vom Rande des Weltraums
- Video: Physics of Sky Diving ("Discovery Education" von youtube: mixx2)
- ZDF - Fliegen im freien Fall Fallschirmspringen
Ein Fallschirmsprung erfolgt im Allgemeinen aus 1000 bis 4500 m über Grund. Der Steigflug im Flugzeug bis in diese Höhe dauert etwa 5 bis 20 Minuten. Im freien Fall werden bei der klassischen Freifallhaltung in Bauchlage innerhalb der ersten 10 Sekunden 300 Höhenmeter überwunden, bis Körpergewicht und Luftwiderstand so gegeneinander wirken, dass die weitere Fallgeschwindigkeit etwa 180 km/h beträgt. Je nach Körperhaltung sind auch höhere Geschwindigkeiten möglich. Bei Tandemsprüngen wird kurz nach dem Absprung ein kleiner Brems- und Stabilisierungsschirm (Drogue) geöffnet, der die Geschwindigkeit nicht über 200 km/h ansteigen lässt. Bei einem Absprung aus 4000 m ist die Öffnungshöhe in etwa 40 bis 60 Sekunden erreicht.
Der Fallschirm wird in der Regel zwischen 1.500 und 700 m über Grund geöffnet. Der Entfaltungsvorgang des Fallschirms dauert zwei bis fünf Sekunden und etwa 200 Höhenmeter, der Schirm hat während des Öffnens eine Bremsbeschleunigung von bis zu etwa 20 m/s². Die anschließende Schirmfahrt dauert etwa 3 bis 5 Minuten mit einer Sinkgeschwindigkeit von etwa 5 m/s. (Aus Wikipedia: Fallschirmspringen)
Links
- Video: Fallen schwere Gegenstände schneller als leichte? (ARD Kopfball vom 27.12.2009)
- Video: APOLLO 15 Hammer and Feather
- Video: the world's biggest vacuum chamber (BBC Two: Brian Cox visits the world's biggest vacuum chamber - Human Universe: Episode 4 Preview - BBC Two)
- Video: Feather and Ball Bearing Dropped in Vacuum (youtube: teralabUK)
- Video: Galileo Galilei und der Freie Fall - Historischer Versuch 4Min.
- Video: Felix Baumgartner - Weltrekord-Sprung vom Rande des Weltraums
- Video: Spektakulär: Video zeigt freien Fall aus 38 km Höhe (Animation)
- Video: Felix Baumgartner - Headcam footage 128k ft space jump HD1080p (Mit Ausschnitten aus Sicht der Helmkamera)
- Video: ZDF - Fliegen im freien Fall Fallschirmspringen
- Video: Movie Park Germany - The High Fall - Free Fall Tower - 11.04.2009 - Jens aus Bielefeld
- Video: ZDF - Fliegen im freien Fall Fallschirmspringen
- Video: Freier Fall im Windkanal (focus.de)]
- Video: Physics of Sky Diving ("Discovery Education" von youtube: mixx2)
- Video: World Champion Freestyle skydiving
- Fall eines Papiertrichters Videoanalyse (Dr. Markus Wey, Gymnasium Kirchenfeld, Schweiz)