Aufgaben zu Energiebilanzen (Lösungen)

Ein LKW im Stadtverkehr

Ein voll beladenener 40-Tonner hält bei seiner Fahrt durch die Stadt an fünf roten Ampeln und beschleunigt jedesmal wieder auf 50 km/h.

• Nach jeder Beschleunigungsphase steckt die Energiemenge

[math]E_{kin}=\frac{1}{2}\, \rm m \ v^2 = \frac{1}{2}\, 40000\, kg \ (13{,}9\, \frac{m}{sec})^2 = 3864000\, J[/math]

in der Bewegung. Für alle fünf Ampeln benötigt er 19321000 Joule, also ca. 19 MJ (MegaJoule).

• Durch den Wirkungsgrad von 1/3 benötigt er eine Dieselmenge mit dem dreifachen Energiegehalt aller Bewegungen, also ca. 58 MJ, was 1 1/2 Litern Diesel entspricht.
• Beträgt seine Masse nur noch die Hälfte, so ist auch nur noch die Hälfte der Energie zum Beschleunigen nötig. Denn die Bewegungsenergie ist proportional zur Masse: [math]E_{kin}=\frac{1}{2}\, m \, v^2[/math]. Deshalb benötigt der LKW auch nur die Hälfte des Treibstoffs.

Beim Klettern

• Elisabeth fällt sechs Meter tief, bis das Seil straff ist. Dabei wandelt sich ihre Lageenergie in Bewegungsenergie um:

[math]E_{pot}= m \, g \, h = 60\,\rm kg \cdot 10\, N/kg \cdot 6\, m = 3600\, Nm = 3600\, J[/math]

Bei ihrer Tochter ist es nur die Hälfte der Energie, also 1800 Joule.

• Man kann ihre Lageenergie der Bewegungsenergie gleichsetzen:

[math]{3600\,\rm J} = \frac{1}{2}\, m \, v^2 [/math]

Daraus folgt:

[math]v = \sqrt{\frac{2 \cdot 3600\,\rm J}{60\,\rm kg}} = \approx 11\,\rm \frac{m}{sec} \approx 40\, km/h[/math]

Der gleiche Rechenweg ergibt, das ihre Tochter genauso schnell fällt! Das weiss man auch schon von der Untersuchung des freien Falls, weil Erikas Trägheit im gleichen Maße abgenommen hat wie ihre Gewichtskraft.

Man erkennt es aber auch an der Energiebilanz:

[math]E_{pot}=E_{kin}[/math]

[math]m \, g \, h = \frac{1}{2}\, m \, v^2 [/math]

Durch Division durch die Masse m kürzt sich nämlich die Masse aus der Rechnung heraus und man erhält als Geschwindigkeit nur in Abhängigkeit von der Fallhöhe:

[math]v= \sqrt{2\, g\, h}[/math].

Beim Radfahren: Unterführung oder Brücke?

• Beim Bergaufrollen wird Energie von der Bewegung auf ihre Lage umgeladen. Beim Bergabrollen umgekehrt.

Rollt Elisabeth unter der Brücke hindurch, so wird sie schneller, bis zum tiefsten Punkt des Weges. Sobald der Weg ansteigt nimmt ihre Geschwindigkeit wieder ab und nach der Unterführung ist sie wieder genausoschnell wie davor.

Rollt sie über die Brücke, so wird sie bis zum höchsten Punkt langsamer um nach der Brücke wieder ihre ursprüngliche Geschwindigkeit zu besitzen.

Im Mittel hat sie daher unter der Brücke eine größere Geschwindigkeit, weswegen sie schneller ist als oben herum!

• Elisabeths Bewegungsenergie beträgt am Anfang:

[math]E_{kin}=\frac{1}{2}\, m \, v^2 = \frac{1}{2} 90\,\rm kg \ \left(5\, \frac{m}{sec}\right)^2 = 1125\, J[/math] .

Bei einem Höhenunterschied von einem Meter erhält oder benötigt sie die Energiemenge:

[math]E_{pot}=m\, g\, h = 90\,\rm kg \cdot 10\, N/kg \cdot 1\, m = 900\, J[/math]

Unter der Brücke hat sie 2025 Joule, auf der Brücke nur 225 Joule. Setzt man dies mit ihrer Bewegungsenergie gleich, so ergibt sich für Ihre Geschwindigkeiten:

[math]2025 J = \frac{1}{2}\, m \, v^2 [/math]

[math]v=\sqrt{\frac{2\cdot 2025\,\rm J}{90\,\rm kg} } \approx 6{,}7\,\rm \frac{m}{sec} \approx 24 \,\frac{km}{h}[/math] und entsprechend auf der Brücke: [math]v \approx 2{,}2\,\rm \frac{m}{sec} \approx 8\, \frac{km}{h}[/math]

• Da bei der Fahrt über die Brücke die auftetenden Geschwindigkeiten geringer sind, ist auch ihr Reibungsverlust geringer und sie benötigt insgesamt weniger Energie. Die Energiespeicherung als Lageenergie ist also effektiver als die Speicherung in der Bewegung!

Eine Federschwingung

Ein Wagen ist durch einer Feder am Tisch befestigt. Der Wagen wird ein Stück nach rechts geschoben und losgelassen.

• Der Wagen wird von der Feder nach links gedrückt bis die Feder entspannt ist. Dann bewegt sich der Wagen aufgrund seiner Trägheit weiter und die Feder zieht an ihm, bis der Wagen stehen bleibt. Danach beschleunigt die Feder den Wagen wieder nach rechts.

Der Wagen schwingt also hin und her!

• Die Energie ist abwechselnd in der zusammengedrückten oder auseinandergezogenen Feder (Spannenergie) und in dem sich bewegenden Wagen (Bewegungsenergie).

• Zur genaueren Beschreibung hat man die Federkonstante zu 0,5 N/cm und die Masse des Wagens zu 100 Gramm bestimmt. Der Wagen wird aus der Position mit entspannter Feder um 2 cm nach rechts ausgelenkt und losgelassen.

Zur Berechnung der Spannenergie in der Feder beträgt muss man Federkonstante und Verkürzung in Standardeinheiten umrechnen:

[math]E_{Sp}=\frac{1}{2}\, D \, s^2 = \frac{1}{2}\, 50 \,\rm \frac{N}{m} \, (0{,}05 \,\rm m)^2 = 0{,}0625 \,\rm Nm = 0{,}0625 \, J[/math]

Setzt man dies der Bewegungsenergie gleich, folgt für die Geschwindigkeit:

[math]\frac{1}{2}\, m \, v^2 = \frac{1}{2}\, 0{,}1 \,\rm kg \, v^2 = 0{,}0625 \, J[/math]

[math]v= \sqrt{\frac{2 \cdot 0{,}0625 \,\rm J}{0{,}1 \,\rm kg}} \approx 1{,}1 \,\rm \frac{m}{sec} = 4\, \frac{km}{h}[/math]

• Wenn sich die träge Masse des Wagens vervierfacht, so muss das Quadrat der Geschwindigkeit nur noch ein Viertel betragen, die Geschwindigkeit also nur noch die Hälfte: [math]v= 2\,\rm \frac{km}{h}[/math].

Drückt man stattdessen die Feder doppeltsoviel zusammen, so vervierfacht sich die Energiemenge:

[math]E_{Sp}=\frac{1}{2}\, D \, (2s)^2= 4\cdot \frac{1}{2}\, D \, s^2 [/math]

Deshalb wird der Wagen auch doppelt so schnell:

[math]E_{kin}=\frac{1}{2}\, m \, (2v)^2 = 4\cdot \frac{1}{2}\, m \, v^2 [/math]

[math]v= 8 \,\rm \frac{km}{h}[/math]

Impuls, Kraft und Energie

1) Beschreibe die folgenden Vorgänge ebenso wie das Kanu-Beispiel.

a) Karl und Karla stehen hintereinander auf einem Skateboard. Karl stößt sich von Karla ab.

Vor dem Losfahren haben Karl und Karla keinen Impuls. Durch das Wegdrücken bekommt Karl Impuls nach links und Karla die gleiche Impulsmenge nach rechts. Die Energie kommt aus Karl und geht in die Bewegung von Karl und Karla. Die Kraft, mit der Karl drückt, gibt an, wie sich der Impuls von den beiden mit der Zeit ändert ("p = F t") und wie sich die Energie von beiden längs des Weges ändert ("E = F s").

b) Antonia steht auf einem Skateboard und stößt sich vom Boden ab.

Der Bewegungspartner von Antonia ist die gesamte Erdkugel. Vor dem Losfahren haben Antonia und die Erde keinen Impuls. Durch das Wegdrücken bekommt Antonia Impuls und die Erde die gleiche Impulsmenge in die entgegengesetzte Richtung. Die Energie kommt aus Antonia und geht in die Bewegung von Antonia und fast nichts in die Bewegung der Erde. (Warum, sieht man bei 2).) Die Kraft, mit der Antonia drückt, gibt an, wie sich der Impuls von den beiden mit der Zeit ändert ("p = F t") und wie sich die Energie von beiden längs des Weges ändert ("E = F s").

c) Anton steht auf dem Boden und springt nach oben.

Wieder ist der Bewegungspartner die Erdkugel. Vor dem Sprung haben Anton und die Erde keinen Impuls. Beim Hochspringen drückt Anton sich nach Oben und die Erde nach unten, wodurch Anton Impuls nach Oben und die Erde die gleiche Impulsmenge nach unten erhält. Die Energie kommt aus Anton und geht in seine Bewegung und fast nichts in die Bewegung der Erde. (Siehe 2).) Bei Antons Sprung setzt er sich nicht nur in Bewegung, sondern er hebt sich auch an. Auch für das Hochheben wird ein Teil seiner Energie benötigt.

2) Beschreibe die Vorgänge mit dem Wasserbehältermodell

a) Karl und Karla stehen hintereinander auf einem Skateboard. Karl stößt sich von Karla ab.

Karl hat eine Masse von 100kg und Karla von 50kg. Karl drückt eine halbe Sekunde lang mit einer Kraft von 60N.

• 

  Vor dem Abdrücken.

• 

  Nach dem Abdrücken.

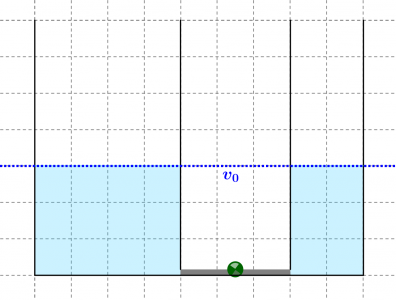
Der Karl entsprechende Wasserbehälter hat eine Grundfläche von 100cm^2, Karlas hat nur die halbe Grundfläche.

Am Anfang sind sie relativ zueinander in Ruhe, deshalb steht das Wasser in beiden Behältern gleichhoch.

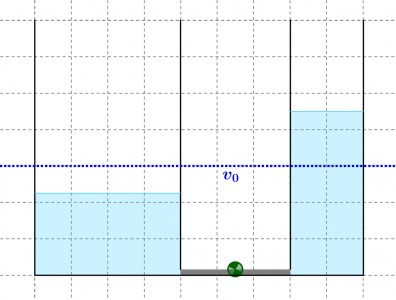
Während des Drückens werden innerhalb von einer halben Sekunde 30ml Wasser von einem Behälter weggenommen und in den anderen transportiert. (Das entspricht 60ml pro Sekunde).

b) Antonia steht auf einem Skateboard und stößt sich vom Boden ab.

Antonia hat eine Masse von 60kg, sie drückt eine Sekunde lang mit 120N. (Die Erde hat eine Masse von ca. 6000000000000000000000000kg = 6*10^24kg.)

• 

  Vor dem Abdrücken.

• 

  Nach dem Abdrücken.

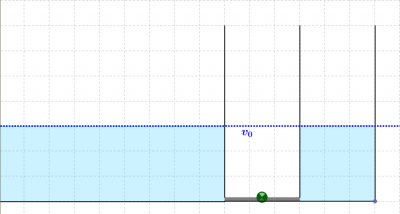
Der Antonia entsprechende Wasserbehälter hat eine Grundfläche von 60cm^2. Der Behälter der Erde eine 10^23 mal so große! (Das sind 600.000.000 Millionen km^2. Die gesamte Wasserfläche der Erde beträgt nur 360 Millionen km^2!) Man kann sich also vorstellen, dass der Wasserbehälter der Erde ein großes Meer oder mindestens ein See ist.

Am Anfang sind sie relativ zueinander in Ruhe, deshalb steht das Wasser in dem Behälter und im See gleichhoch.

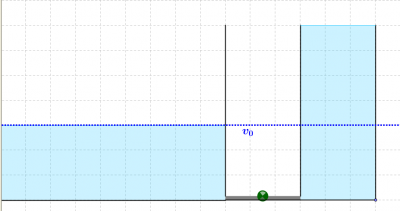
Während des Drückens werden innerhalb von einer Sekunde 120ml Wasser aus dem See weggenommen und in den Behälter transportiert.

c) Anton steht auf dem Boden und springt nach oben.

Anton hat eine Masse von ebenfalls 60kg und drückt beim Absprung eine halbe Sekunde lang mit einer Kraft von 1000N.

Der Anton entsprechende Wasserbehälter hat eine Grundfläche von 60cm^2. Dem der Erde entprechende Behälter ist wieder ein großer See.

Am Anfang sind sie relativ zueinander in Ruhe, deshalb steht das Wasser in dem Behälter und im See gleichhoch.

Auch wenn Anton nur steht und nicht springt muss er mit 600N gegen den Boden drücken, denn das entspricht seiner Gewichtskraft. Drückt er nun mit 1000N, so führen nur die zusätzlichen 400N zu einer Bewegung.

Während des Drückens werden innerhalb von einer halben Sekunde 200ml Wasser aus dem See weggenommen und in den Behälter transportiert. (Das entspricht 400ml pro Sekunde.)

3) Berechnung von Energie und Impulsmengen

Die Kraft gibt gerade die zeitliche Änderung des Impulses an ([math]F=\frac{p}{t}[/math]), die Impulsmenge ergibt sich aus:

[math]p=F\, t[/math].

Die Energiemenge der Bewegung hängt direkt mit der Impulsmenge und der Masse zusammen:

[math]E_{kin} = \frac{p^2}{2\, m} \quad \left(= \frac{1}{2}\, p\, v = \frac{1}{2}\, m\, v^2 \right)[/math].

a) Karl und Karla stehen hintereinander auf einem Skateboard. Karl stößt sich von Karla ab.

Karl hat eine Masse von 100kg und Karla von 50kg. Karl drückt eine halbe Sekunde lang mit einer Kraft von 60N.

Impuls: [math]p=F\, t = 60\, \rm N \cdot 0{,}5\, sec = 30\, Hy[/math].

Bewegungsenergie von Karl: [math]E_{kin} = \frac{p^2}{2\, m} = \frac{(30\,\rm Hy)^2}{2\cdot 100\,\rm kg} = 4{,}5\,\rm J[/math].

Bewegungsenergie von Karla: [math]E_{kin} = \frac{p^2}{2\, m} = \frac{(30\,\rm Hy)^2}{2\cdot 50\, \rm kg} = 9\,\rm J[/math].

Karla hat doppelt so viel Bewegungsenergie wie Karl! Das liegt an ihrer kleineren Masse.

Im Wasserbehältermodell ist klar, warum: Füllt man einen breiten und einen schmalen Behälter mit jeweils der gleichen Wassermenge, so steht das Wasser in dem schmalen Behälter viel höher. Deshalb benötigt man bei dem schmalen Behälter auch mehr Energie, um die gleiche Wassermenge einzufüllen!

b) Antonia steht auf einem Skateboard und stößt sich vom Boden ab.

Antonia hat eine Masse von 60kg, sie drückt eine Sekunde lang mit 120N. (Die Erde hat eine Masse von ca. 6000000000000000000000000kg = 6*10^24kg.)

Impuls: [math]p=F\, t = 120\, \rm N \cdot 1\, sec = 120\, Hy[/math].

Bewegungsenergie von Antonia: [math]E_{kin} = \frac{p^2}{2\, m} = \frac{(120\,\rm Hy)^2}{2\cdot 60\, kg} = 240\,\rm J[/math].

Bewegungsenergie der Erde: [math]E_{kin} = \frac{p^2}{2\, m} = \frac{(120\,\rm Hy)^2}{2\cdot 6\cdot 10^{24}\, \rm kg} = 0\,\rm J[/math].

Die Erde bekommt zwar die gleiche Impulsmenge wie Antonia, aber wegen ihrer riesigen Masse keine Energie!

c) Anton steht auf dem Boden und springt nach oben.

Anton hat eine Masse von ebenfalls 60kg und drückt beim Absprung eine halbe Sekunde lang mit einer Kraft von 1000N.

Auch wenn Anton nur steht und nicht springt muss er mit 600N gegen den Boden drücken, denn das entspricht seiner Gewichtskraft. Drückt er nun mit 1000N, so führen nur die zusätzlichen 400N zu einer Bewegung.

Impuls: [math]p=F\, t = 400\, \rm N \cdot 0{,}5\, sec = 200\, Hy[/math].

Bewegungsenergie von Anton: [math]E_{kin} = \frac{p^2}{2\, m} = \frac{(200\,\rm Hy)^2}{2\cdot 60\, kg} = 333\,\rm J[/math].

Bewegungsenergie der Erde: [math]E_{kin} = \frac{p^2}{2\, m} = \frac{(200\,\rm Hy)^2}{2\cdot 6\cdot 10^{24}\, \rm kg} = 0\,\rm J[/math].

Die Erde bekommt zwar die gleiche Impulsmenge wie Anton, aber wegen ihrer riesigen Masse keine Energie!

(Die Berechnung von Antons Lageenergie ist etwas schwieriger.)