Aufgaben zu Kreisbewegungen (Lösungen)
(Klassische Mechanik > 'Kreisbewegungen)
Inhaltsverzeichnis
"Drehgeschwindigkeiten"
Karussell fahren
Lea, Martin und Karin fahren Karussell. Lea steht ziemlich weit Innen, nur 0,5 Meter von der Drehachse entfernt. Martin steht einen Meter und Karin ganz außen 1,5 Meter entfernt.
Ihre Eltern haben beobachtet, dass das Karussell sich in 2 Sekunden einmal dreht. Sie überlegen jetzt: "Wie schnell ist meine Tochter und mein Sohn?"
- Berechne die Frequenz, die Bahngeschwindigkeit und die Winkelgeschwindigkeit der drei und gib den Eltern eine Antwort.
- Alle Kinder sind in dem Sinne "gleichschnell", dass ihre Frequenz, Umlaufdauer und Winkelgeschwindigkeit gleichgroß sind.
- Ihre Bahngeschwindigkeiten sind aber unterschiedlich: Je weiter außen, desto schneller.
- Die Winkelgeschwindigkeit entspricht genau der Bahngeschwindigkeit bei einem Meter Radius! Sie ist eine "normierte Bahngeschwindigkeit".
- Die Frequenz beträgt eine halbe Umdrehung pro Sekunde:
- [math]f=\frac{1}{T}=\frac{1}{2 \,\rm sec}= 0,5 \, \frac{1}{\rm sec}=0{,}5 \,\rm Hz [/math]
- Die Winkelgeschwindigkeit ist gerade [math]\pi[/math] pro Sekunde:
- [math]\omega = 2\pi f = \frac{2 \pi}{T} = 2\pi \cdot 0{,}5 \frac{1}{\rm sec} = \pi \frac{1}{\rm sec}\approx 3 \frac{1}{\rm sec}[/math]
- Die Bahngeschwindigkeiten nehmen mit jedem 1/2 Meter um 1,5 m/sec zu:
- Lea: [math]v=\omega \, r = 3,14 \frac{1}{\rm sec}\cdot 0{,}\,\rm 5\, m \approx 1,5\frac{\rm m}{\rm sec}[/math]
- Martin: [math]v=\omega \, r = 3{,}14 \frac{1}{\rm sec}\cdot 1\,\rm m \approx 3 \frac{\rm m}{\rm sec}[/math]
- Karin: [math]v=\omega \, r = 3{,}14\frac{1}{\rm sec}\cdot 1{,}5\,\rm m \approx 4,5 \frac{\rm m}{\rm sec}[/math]
Plattenspieler und CD-Spieler
Ein Plattenspieler hat eine Frequenz von 33 oder 45 Umdrehungen pro Minute.
- Wie groß ist die Bahngeschwindigkeit am Ort der Abtastnadel? Der Abstand zwischen Nadel und der Mitte der Platte variiert dabei zwischen 5 und 20 cm.
- Zunächst kann man für die verschiedenen "Drehgeschwindigkeiten" die Frequenz in Hertz berechnen:
- [math]f_1 = 33\rm \, \frac{1}{min} = 33\rm \, \frac{1}{60\,s} = 0{,}55\rm \, Hz[/math]
- [math]f_2 = 45\rm \, \frac{1}{min} = 45\rm \, \frac{1}{60\,s} = 0{,}75\rm \, Hz[/math]
- Daraus kann man dann die Winkelgeschwindigkeiten bestimmen:
- [math]\omega_1 = 2\, \pi \, f_1 = 3{,}46\rm\,Hz [/math]
- [math]\omega_1 = 2\, \pi \, f_1 = 4{,}71\rm Hz [/math]
- Die Bahngeschwindigkeiten ergeben sich aus der Winkelgeschwindigkeit in Abhängigkeit vom Radius:
- [math]v_{1min}=\omega_1 \, r= 3{,}46\frac{1}{s} \cdot 5\rm\,cm = 17{,}3\rm\,\frac{cm}{s}[/math]
- [math]v_{2min}=\omega_2 \, r= 4{,}71\frac{1}{s} \cdot 5\rm\,cm = 23{,}6\rm\,\frac{cm}{s}[/math]
- [math]v_{1max}=\omega_1 \, r= 3{,}46\frac{1}{s} \cdot 20\rm\,cm = 69{,}1\rm\,\frac{cm}{s}[/math]
- [math]v_{2max}=\omega_2 \, r= 4{,}71\frac{1}{s} \cdot 20\rm\,cm = 94{,}2\rm\,\frac{cm}{s}[/math]
Eine Audio-CD wird von einem Laser abgetastet. Dabei wird sie so gedreht, dass sie eine konstante Bahngeschwindigkeit von 1,2 m/sec am Laser hat. (Wikipedia: CD-Lesevorgang)
- Wie schnell muss man am Anfang der Spur r= 3cm und am Ende r= 8cm drehen? Gib die Winkelgeschwindigkeit, die Frequenz und die Umlaufdauer an.
- Die Bahngeschwindigkeit hängt von der Winkelgeschwindigkeit und vom Radius ab:
- [math]v=\omega \, r \quad \Rightarrow \quad \omega = \frac{v}{r} =\frac{1{,}2\rm\,\tfrac{m}{s}}{0{,}03\rm\,m} = 40\rm\,\frac{1}{s}=40\rm\,Hz[/math]
- Aus der Winkelgeschwindigkeit berechnet sich die Frequenz:
- [math]\omega=2\,\pi\,f \quad \Rightarrow \quad f= \frac{\omega}{2\,\pi} =\frac{40\rm\,Hz}{2\,\pi} = 6{,}37\rm\,Hz[/math]
- Aus der Winkelgeschwindigkeit oder Frequenz berechnet sich dann die Umlaufdauer:
- [math]\omega=\frac{2\,\pi}{T} \quad \Rightarrow \quad T= \frac{2\,\pi}{\omega}= \frac{1}{f}= \frac{1}{6{,}37\rm\,\tfrac{1}{s}}= 0{,}157\rm\,s[/math]
- Für den größeren Radius von 8cm ergeben sich die Werte nach der gleichen Rechenmethode. (Wegen den (Anti-)Proportionalitäten kann man das auch mit einem Dreisatz ausrechnen.):
- [math]\omega =15\rm\,Hz[/math]
- [math]f= 2{,}39\rm\,Hz[/math]
- [math]T = 0{,}419\rm\,s[/math]
- Tastet man die CD außen ab muss sie sich also langsamer drehen.
Eine Uhr
- Wie groß sind die Frequenz, die Umlaufdauer und die Winkelgeschwindigkeit von Stunden-, Minuten- und Sekundenzeiger einer Uhr?.
- Die Umlaufdauer der Zeiger sind klar:
- Sekundenzeiger: [math]T_s=1\rm\, min=60\rm\,s[/math]
- Minutenzeiger: [math]T_{min}=1\rm\, h=3600\rm\,s[/math]
- Stundenzeiger: [math]T_h=12\rm\, h = 43200\rm\,s[/math]
- Daraus berechnet sich die Frequenz mit [math]f=\frac{1}{T}[/math]:
- Sekundenzeiger: [math]f_s=0{,}0167\rm\,Hz[/math]
- Minutenzeiger: [math]f_{min}=0{,}000278\rm\,Hz=0{,}278\rm\, mHz[/math]
- Stundenzeiger: [math]f_h=0{,}0000231\rm\,Hz=23{,}1\rm\, \mu Hz[/math]
- Entweder aus der Frequenz oder aus der Umlaufdauer ergibt sich die Winkelgeschwindigkeit mit [math]\omega=2\,\pi\f=\frac{2\,\pi}{T}[/math]
- Sekundenzeiger: [math]\omega_s=0{,}105\rm\,Hz[/math]
- Minutenzeiger: [math]\omega_{min}=0{,}00175\rm\,Hz=1{,}75\rm\, mHz[/math]
- Stundenzeiger: [math]\omega_h=0{,}000145\rm\,Hz=145\rm\, \mu Hz[/math]
Kosmische Geschwindigkeiten
Bekanntermaßen dreht sich die Erde einmal in 24 Stunden um sich selbst.
- Wie schnell ist deswegen eine Person, die am Äquator steht? (Und in Freiburg?)
- Der Erdumfang beträgt ca. 40 Millionen Meter[1]. Dementsprechend beträgt die Bahngeschwindigkeit am Äquator:
- [math]v_{Äqu}=\frac{U}{T}=\frac{40\cdot10^{6}\rm\,m}{24\rm\,h}=\frac{40\cdot10^{6}\rm\,m}{24\cdot 60 \cdot 60 \rm\,s}=463\rm\frac{m}{s}=1667\rm\,\frac{km}{h}[/math]
- Das ist mehr als Schallgeschwindigkeit!
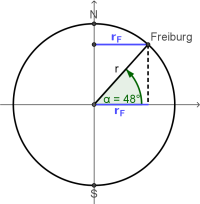
- In Freiburg bewegt man sich aber auf einer Kreisbahn mit einem kleineren Radius, denn Freiburg befindet sich ungefähr auf dem 48ten nördlichen Breitengrad:
- [math]\cos(\alpha)=\frac{r_F}{r}\quad \Rightarrow \quad r_F = r \, \cos(\alpha) = 6350\rm\,km \cdot cos(48^\circ) = 4250\rm\,km[/math]
- Damit ergibt sich die Bahngeschwindigkeit:
- [math]v_{F}=\frac{U_F}{T}=\frac{2\pi\cdot 4250\rm\,km}{24\rm\,h}=\frac{26{,}7\cdot10^{6}\rm\,m}{86400 \rm\,s}=309\rm\frac{m}{s}=1110\rm\,\frac{km}{h}[/math]
- Das ist immer noch ungefähr Schallgeschwindigkeit.
- Man kann die Bahngeschwindigkeit auch allgemein in Abhängigkeit des Breitengrades berechnen:
- [math]v(\alpha)=\frac{U(\alpha)}{T}=\frac{2\pi \, r(\alpha)}{T}=\frac{2\pi \, r \cos(\alpha)}{T}=\frac{2\pi \, r }{T}\cos(\alpha)[/math]
Die Erde dreht sich in 365 Tagen einmal um die Sonne.
- Wie schnell sind wir aufgrund der Bewegung der Erde um die Sonne?
- Die Erde bewegt sich näherungsweise auf einer Kreisbahn mit einem Radius von 149,6 Mio km[2] in 365,27 Tagen um die Sonne.
- [math]v_{E}=\frac{U}{T}=\frac{2\pi\cdot 149{,}6\cdot10^{6}\rm\,km}{365{,}27\rm\,d}=\frac{2\pi\cdot 149{,}6\cdot10^{9}\rm\,m}{365{,}27\cdot 24 \cdot 60 \cdot 60 \rm\,s}=\frac{937{,}9\cdot10^{9}\rm\,m}{31{,}56\cdot 10^{6} \rm\,s}=29700\rm\frac{m}{s}=29{,}7\rm\frac{km}{s}=107000\rm\,\frac{km}{h}[/math]
- Das ist schnell, aber nur 0,01% der Lichtgeschwindigkeit.
Impuls, Kraft und Energie
Karussell fahren II
Lea, Martin und Karin fahren Karussell. Ihr Ball stört Karin beim Karussellfahren. Deshalb möchte sie ihn ihrem Vater geben, der gut darauf aufpassen soll. Sie schaut, wo ihr Vater steht und läßt den Ball los, als sie ihren Vater sieht. Voll daneben!
- Mache eine Zeichnung von dem Vorgang aus der Vogelperspektive und erkläre, wann Karin hätte loslassen müssen.
- Das Verhalten des Balles läßt sich mit dem Trägheitsgsetz erklären: Der Ball behält nach dem Loslassen seinen Impuls bei, weil ihn keine Kraft mehr auf der Kreisbahn hält. Er fliegt tangential zur Bahnkurve weiter. Karin muss also eine 1/4 Umdrehung vorher loslassen!
Karin sagt ihren Eltern, dass sie im Karussell ganz arg nach außen gezogen wird und sie sich deshalb gut festhalten muss. Ihre Mutter entgegnet ihr, dass sie nur gesehen hat, dass Karin sich festgehalten hat.
- Erkläre der Mutter warum beide Recht haben, indem du beschreibst wie aus Karins Sicht Kräfte den Impuls verändern und wie das aus der Sicht der Mutter ist.
- Beide Sichtweisen sind richtig und zeigen, dass in verschiedenen Bezugssystemen bei der gleichen Bewegung unterschiedliche Kräfte wirken können.
- Aus Sicht der Mutter ändert Karins Impuls ständig die Richtung. Die Richtungsänderung erreicht Karin durch das Ziehen nach Innen ("Zentripetalkraft").
- Aus der Sicht von Karin ändert sich ihr Impuls nicht, sie verharrt auf der gleichen Stelle des Karussells.
- Die Summe der auf sie wirkenden Kräfte ist daher Null! Die sie nach außen ziehende Trägheitskraft ("Zentrifugalkraft") gleicht sie durch das Ziehen nach Innen aus.
- Die wirkenden Kräfte in den verschiedenen Bezugssystemen kann man in dieser Animation sehen.
Lea steht ziemlich weit Innen, nur 0,5 Meter von der Drehachse entfernt. Martin steht einen Meter und Karin ganz außen 1,5 Meter entfernt. Ihre Eltern haben beobachtet, dass das Karussell sich in 2 Sekunden einmal dreht.
- Mit welcher Kraft müssen sich Lea, Martin und Karin festhalten? (Schätze fehlende Angaben.)
- Je größer die Masse der Kinder, desto stärker müssen sie sich festhalten. Ich nehme für alle drei Kinder an, sie hätten eine Masse von 30 kg.
- Für die Stärke der Zentripetal- und Zentrifugalkraft gilt:
- [math]F_Z=\frac{m\,v^2}{r}=m\, \omega^2 \, r[/math] Für diesen Fall mit gleicher Winkelgeschwindigkeit ist die zweite Formel praktischer:
- Lea: [math]F_Z= 30\,\rm kg \cdot (3,14 \frac{1}{sec})^2 \cdot 0,5 \, m = 150 \, N[/math]
- Martin: [math]F_Z= 30\,\rm kg \cdot (3{,}14 \frac{1}{sec})^2 \cdot 1 \, m = 300 \, N[/math]
- Karin: [math]F_Z= 30\,\rm kg \cdot (3{,}14 \frac{1}{sec})^2 \cdot 1{,}5 \, m = 450 \, N[/math]
- Bei Martin wirkt also eine Beschleunigung, die gerade der Erdbeschleunigung entspricht. Er muss genauso stark ziehen, als ob er sich einer einer Reckstange hochziehen würde.
- Karin muss sogar mit ihrer 1,5 fachen Gewichtskraft ziehen!
Links
- Wikipedia: CD-Lesevorgang
- Landesbildungsserver BaWü: Datenaufzeichnung und Kreisbewegung; Die Technik der Aufzeichnung von Musik und Daten hat (fast) immer mit Kreisbewegung zu tun.
Fußnoten
- ↑ Das ist kein Zufall, sondern liegt an der ursprünglichen Definition des Meters während der französischen Revolution.
- ↑ Wikipedia: Erdbahn