Flächenladungsdichte, elektrische Feldkonstante und erste Maxwellsche Gleichung

Inhalt Kursstufe > Das elektrische Feld

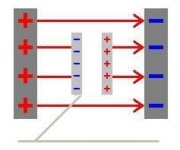
Versuch: Influenzierte Platten im Kondensator

Aufbau

Die beiden Platten liegen unter dem Kondensator. Rechts der Messverstärker mit Voltmeter als Anzeige.

Ein Kondensator ist an eine Hochspannungsquelle angeschlossen.

Zwei Metallplatten, die an Plastikstäben befestigt sind, werden zwischen den Kondensator geführt. Während diesem Vorgang berühren sich die Innenseiten der Platten noch. Im Feld werden die Platten dann getrennt und mit etwa einem Zentimeter Abstand aus dem Feld herausgeführt.

Nun werden sie nacheinander, also einzeln an den Messverstärker gehalten.

Danach trennt man den Kondensator von der Spannungsquelle und bestimmt die Ladung der Kondensatorplatten.

Beobachtung

Hält man die rechte Platte an den Verstärker, so schlägt er positiv aus. Hält man danach die linke daran, so geht der Ausschlag auf null zurück.

• U = 5kV d = 5cm Q = 8 nC
• U = 10kV d = 5cm Q = 17 nC
• U = 15kV d = 5cm Q = 25 nC

Bestimmt man die Flächenladungsdichte der Kondensatorplatte, so stellt man fest, dass diese mit der Dichte auf den influenzierten Platten übereinstimmt! Weitere Messwerte:

• U = 5kV d = 7cm Q = 4nC
• U = 10kV d = 7cm Q = 8nC
• U = 15kV d = 7cm Q = 12nC
• U = 5kV d = 3,5cm Q = 8nC

Vor allem an dem letzten Messwert kann man nun zusätzlich ablesen, dass nicht nur die Spannung maßgeblich für die Feldstärke ist, sondern auch der Abstand zwischen den Kondensatorplatten.

Erklärung

Zwei influenzierte und auseinandergezogene Platten im elektrischen Feld.

Die Platten werden im Feld influenziert,es baut sich ein Gegenfeld auf, sodass der Raum zwischen den Platten feldfrei ist. An den der Kondensatorplatten zugewandten Oberflächen der Platten befinden sich Ladungen.

• Die influenzierte Ladungsmenge ist proportional zur Feldstärke. [math]Q \sim E[/math]
• Die Ladungsmenge ist außerdem proportional zur Fläche der Platten. [math]Q \sim E \, A[/math]
• Die Flächenladungsdichte ist daher proportional zur Feldstärke. [math]\frac{Q}{A}\sim E[/math]
• Den Proportionalitätsfaktor nennt man elektrische Feldkonstante [math]\epsilon_0[/math].

[math]\sigma = \frac{Q}{A} = \varepsilon_0 \, E[/math]

Da der Kondensator die gleiche Flächenladungsdichte aufweist, kann man die obige Formel nun auf zweierlei Arten interpretieren:

Ein elektrisches Feld erzeugt eine bestimmte influenzierte Flächenladungsdichte

[math]\frac{Q}{A}=\varepsilon_0 E[/math]

Eine Flächenladungsdichte erzeugt eine bestimmte Feldstärke

[math]E=\frac{1}{\varepsilon_0}\frac{Q}{A}[/math]

Dieses Ergebnis stimmt mit den vorher qualitativ betrachteten Ladungsverteilungen in geladenen Körpern überein. An den Stellen, an denen sich viele Ladungen auf der Oberfläche sammeln ist die Feldstärke groß und umgekehrt. (Vgl. die Bilder von Ladungsverteilungen.)

Die elektrische Polarisation P

Wie stark ein Körper durch ein elektrisches Feld "elektrisiert", also influenziert wird, kann man mit Hilfe der Flächenladungsdichte nun beschreiben.

Die Möglichkeit einen Gegenstand vom elektrischen Feld influenzieren zu lassen erlaubt es das elektrische Feld selbst zu untersuchen. Diese Feldgröße heißt elektrische Polarisation.

[math]P=\frac{Q}{A}[/math]

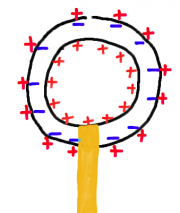
Versuch: Influenzierte Hohlkugel (Cavendish)

Aufbau

Hier wird ein abgeschirmtes Kabel zur Messung der Ladung verwendet.

• Man lädt die Kugel mit Hilfe des Hochspannungsnetzgerätes auf.
• Dann nähert man die äußeren Kugelschalen ohne dass sie die innere Kugel berühren.
• Man misst die Ladung der äußeren Kugelschale.
• Man misst die Ladung der inneren Kugel.

Beobachtung

• Die Kugelschalen sind auf der äußeren Seite mit der gleichen Ladungsmenge versehen wie die innere Kugel.
• Einen ähnlichen Versuch der ETH Zürich sieht man auf diesem Video.

(Bei U= V misst man ? )nC.

Erklärung

Die äußere influenzierte Kugelschale trägt die gleiche Ladungsmenge an ihrer Außenseite wie die innere Kugel.

Die äußere Kugelschale wird im Feld der inneren Kugel influenziert.

Da die innere Kugel eine kleinere Oberfläche hat als die äußere, aber die gleiche Ladungsmenge trägt, kann man daraus schließen, dass die Flächenladungsdichte der äußeren Kugel geringer ist. Daraus folgt wiederum, dass die Feldstärke abgenommen hat!

Daraus kann man die Feldstärke des Zentralfeldes in Abhängigkeit von der felderzeugenden Ladung, also im wesentlichen das Coulombsche Kraftgesetz bestimmen:

[math] \frac{Q}{A}=\varepsilon_0 E[/math]

Setzt man die Kugeloberfläche [math]A=4\, \pi r^2[/math] ein und löst nach der Feldstärke auf, ergibt sich:

[math]E=\frac{1}{\varepsilon_0} \, \frac{Q}{A} = \frac{1}{4 \pi \varepsilon_0}\, \frac{Q}{r^2}[/math]

Nun wird auch klar, warum die Proportionalitätskonstante im Coulombschen Gesetz gerade [math]\frac{1}{4 \pi \varepsilon_0}[/math] ist!

Felderzeugende Ladung und Feldstärke (Erste Maxwellsche Gleichung)

Die Ergebnisse des Cavendish-Experiments lassen sich auf zwei Weisen anwenden:

• Man kann bei bekannter Ladungsmenge die mittlere Feldstärke durch eine Fläche bestimmen.
• Man kann bei bekannter mittlerer Feldstärke durch eine geschlossene Fläche auf die Ladung innerhalb der Fläche rückschließen.

Waren die Flächen beim Cavendish-Experiment Kugelschalen, so läßt sich das verallgemeinern:

1. Man kann beliebige Äquipotentialflächen verwenden.
2. Man kann sogar beliebige, geschlossene Flächen verwenden.
3. Bei einer nicht konstanten Feldstärke rechnet man mit dem senkrechten Anteil der mittleren Feldstärke [math]\bar E[/math].

[math]Q = \epsilon_0 \, \bar E \, A[/math]

Auf diese elegant formulierte Art wird eindrücklich klar, dass die Ladungen Quellen und Senken des elektrischen Feldes sind. Es ist eine verallgemeinerte Version der Feldstärke des Zentralfeldes.

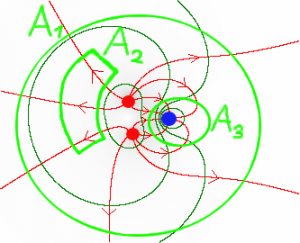
Allgemeine Beispiele

Die umschlossene Ladungsmenge und die mittlere Feldstärke durch die gewählte Fläche hängen direkt zusammen. Je nach Wahl der Fläche lassen sich verschiedene Aussagen machen.

A1: Die mittlere Feldstärke entspricht einer positiven Ladung.

A2: Die mittlere Feldstärke ist Null, die Fläche enthält keine Ladung.

A3: Die mittlere Feldstärke enstpricht einer negativen Ladung.

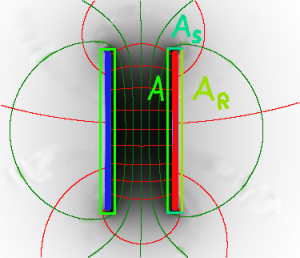
Anwendung beim Kondensator

Legt man um die positiv geladene Platte eine Fläche, so laufen die Feldlinien aus der Fläche heraus, die enthaltene Ladung ist positiv. Bei der negativen Platte laufen die Feldlinien herein, die Ladung ist negativ.

Quantitativ erhält man den bereits bekannten Zusammenhang zwischen der Kondensatorfläche, der Feldstärke und der Ladung.

Die Feldstärke an den Rückseiten des Kondensators beträgt fast Null und wird vernachlässigt. Somit ist auch der elektrische Fluss durch die Aussenfläche A_R Null. Der Fluss durch die Seitenflächen A_S verschwindet fast, weil die Flächen sehr klein sind.

Man erhältfür die positive Platte:

[math]A[/math]: Kondensatorfläche

[math]E[/math]: Feldstärke im Kondensator

[math]E_S[/math]: Feldstärke an den Seiten

[math]E_R[/math]: Feldstärke an der Rückseite

[math]Q=\varepsilon_0 \, \bar E \, A_{ges} = \varepsilon_0 \,(E \, A + E_S\, A_S + E_K\, A_K) = \varepsilon_0 \, E \, A[/math]

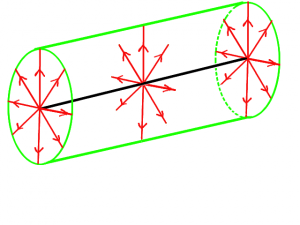
Feld eines geladenen langen Drahtes (Zylinderfeld)

Denkt man sich den Cavendish-Versuch für einen langen, geladenen Draht, so läßt sich seine Feldstärke bestimmen.

Der Draht habe die Länge l und sei mit der Ladung Q geladen.

Man legt eine Zylinderfläche um den Draht, die aus Symmetriegründen auch Äquipotentialfläche ist. Die kreisförmigen Abschlüsse des Zylinders vernachlässigt man, weil man von einem relativ langen Draht ausgeht und die Flächen somit im Vergleich zur Mantelfläche sehr klein sind. Der elektrische Fluss durch diese Flächen "ist Null".

Nun gilt:

[math]A=2\pi \, r \, l[/math] (Mantelfläche des Zylinders)

[math]E=\frac{1}{\varepsilon_0} \, \frac{Q}{A} = \frac{1}{\varepsilon_0} \, \frac{Q}{2\pi r l}[/math]

[math]E=\frac{1}{\varepsilon_0 2\pi \, l} \, \frac{Q}{r}[/math]

Die Feldstärke nimmt also nur proportional zu [math]\frac{1}{r}[/math] ab und nicht wie beim Zentralfeld proportional zu [math] \frac{1}{r^2}[/math]!

Man sagt, das Feld hat eine größere Reichweite.

Für das Potential ergibt sich eine interessante Folgerung. Da es die Aufleitung (Stammfunktion) der Feldstärke ist, hat das Potential die Form:

[math]\varphi(r)=\mathrm{c} \cdot \ln(r) [/math]

Beim Gravitationsfeld der Erde kann man für einen Körper eine Fluchtenergie bestimmen, mit der er das Feld der Erde langfristig verlässt. Aus dem logarithmischen Potential kann man schließen, dass eine Ladung mit einer gewissen Anfangsenegie dem Feld des geraden Leiters nicht entkommen kann. Auch so kann man den Begriff "größere Reichweite" interpretieren.

Links

• Video: Influenzierte Hohlkugel, Gesetz von Gauss 1 (Vorlesungsexperiment der ETH Zürich)