Kraft und Impuls

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche

(Kursstufe > Mechanik)

(Klassische Mechanik > Dynamik - Trägheit und wie man sie überwindet)


Wesentlich für das Verständnis der Newtonschen Mechanik ist die Massenträgheit. Ein Gegenstand ändert seine Bewegung nur, wenn jemand oder etwas mit einer Kraft an ihm zieht oder drückt. Die Bewegung eines Gegenstandes lässt sich in eine Translation durch den Raum und eine Rotation um die Drehachse aufteilen.

Dementsprechend muss man mit einer Kraft drücken oder ziehen für das Beschleunigen, das Bremsen und die Richtungsänderung sowohl der Translation als auch der Rotation.


Massenträgheit und Bewegungsmenge

Massenträgheit (1. Newtonsches Axiom)

  • Ein Körper behält seine Bewegung bei, solange keine Kraft auf ihn wirkt. Die Bewegung wird durch die Menge an Impuls [math]\vec p[/math] (Schwung) für die Translation und Drehimpuls [math]\vec L[/math] (Drehschwung) für die Rotation angegeben. Sowohl Impuls als auch Drehimpuls haben eine Richtung und sind vektorielle Größen.
  • In der Schulphysik wird die Rotation von Gegenständen in der Regel vernachlässigt, man betrachtet nur die Translation.
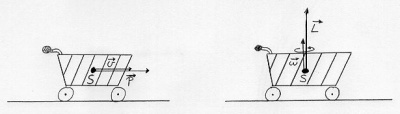
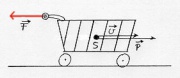
  • Beispiel mit reibungsarmen Einkaufswagen: Nach dem "Anschubsen" bewegt sich der Wagen ohne weitere Einwirkung geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht.

Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn.

(Dreh-)Impuls und (Winkel-)Geschwindigkeit

Die Bewegungsmenge eines Einkaufswagens.
  • Ein Körper enthält viel Impuls, wenn er schnell ist und eine große Masse hat. Man legt den Impuls daher als Produkt der beiden Größen fest. Damit sind der Impuls- und Geschwindigkeitsvektor zueinander parallel und die Masse ist der Proportionalitätsfaktor:
[math]\vec p = m \, \vec v[/math]
Leider hat die Einheit des Impulses keinen allgemeingültigen eigenen Namen bekommen, im Karlsruher Physikkurs wird sie nach Christiaan Huygens benannt.
[math][\vec p] = \mathrm{1kg \frac{1m}{1s} = 1Hy}[/math] (lies: Huygens)
  • Der Drehimpulsvektor und die Winkelgeschwindigkeit sind ebenfalls parallel und der Proportionalitätsfaktor ist das Trägheitsmoment des Körpers:
[math]\vec L = \Theta \, \vec \omega[/math][1]
  • Sind die Masse und das Trägheitsmoment zeitlich konstant, kann man die Bewegung eines Gegenstandes auch über seine Geschwindigkeit und Winkelgeschwindigkeit beschreiben.

Zusammenhang zwischen Kraft und Impuls

Änderung der Bewegungsmenge (2. Newtonsches Axiom)

  • Eine Kraft kann die Bewegungsmenge verändern und wenn die Bewegungsmenge sich verändert muss eine Kraft wirken.

Die Kraft ist die zeitliche Änderungsrate des Impulses und gibt an,
wieviel Impuls in einen Körper pro Zeit hinein oder herausfließt:

[math]\vec F = \dot {\vec p} \approx \frac{\triangle \vec p}{\triangle t} \quad \mathrm{("Impulsstromstärke") } \qquad [\vec F] = \mathrm{1N = \frac{1Hy}{1s} = \frac{1kg \,m}{s^2} }[/math]

Wenn die Masse des Körpers sich nicht verändert ,
ist die Kraft proportional zur Änderung der Geschwindigkeit und
die (träge) Masse der Proportionalitätsfaktor:

[math]\vec F = m\, \dot{\vec v} = m \,\vec a \approx m \, \frac{\triangle \vec v}{\triangle t}[/math]
Eine Veränderung der Bewegungsmenge durch eine Kraft. Der Wagen wird langsamer.
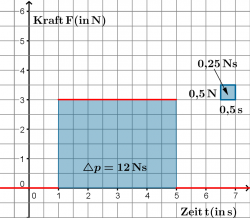
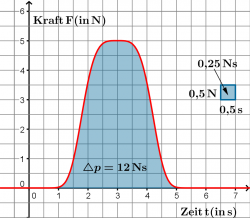
  • Wird an einem Gegenstand mit einer Kraft von 3N gezogen oder gedrückt, so fließen pro Sekunde 3Hy Impuls hinein. In vier Sekunden also 12 Hy Impuls.
  • Eine Kraft mit der Stärke 10N beschleunigt einen Körper der Masse 5kg in einer Sekunde um 2m/s.
Die Fläche unter dem Kraft-Zeit-Graphen entspricht der Impulsänderung. Hier entspricht ein Kästchen 0,25 Hy Impuls.
Das gilt auch bei nicht konstanten Kräften. Man zählt ungefähr 48 Kästchen.

skalar auf einer Geraden

Beim freien Fall kommt pro Zeiteinheit immer die gleiche Impulsmenge in Richtung der wirkenden Kraft dazu.

vektoriell

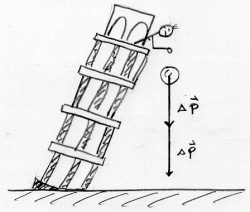
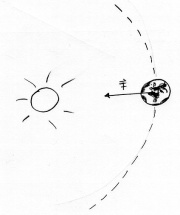Bei der Kreisbewegung wirkt die Kraft immer senkrecht zur Bewegungsrichtung. So ändert sich die Richtung des Impulses, aber nicht der Betrag.
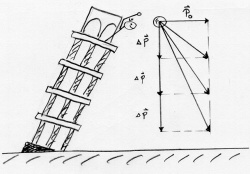Beim einem Wurf bleibt der horizontale Anteil des Impulses konstant. Nur der Impulsanteil nach unten ändert sich.

Wechselwirkung von Körpern

"Actio gleich reactio" / Impulserhaltung (3. Newtonsches Axiom)

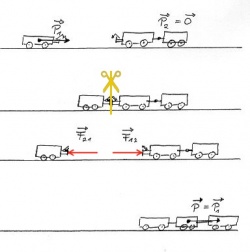
Ändert ein Gegenstand seinen Impuls, so ist immer auch ein Partner beteiligt.

Stößt sich der Gegenstand mit der Kraft [math]\vec F[/math] ab, so wirkt die Gegenkraft [math]-\vec F[/math] auf den Partner.

Sowohl die Summe der Impulse als auch die Bewegung des gemeinsamen Schwerpunkts bleiben erhalten.

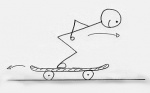
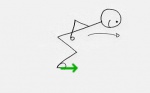
  • Ein Mensch springt von einem Skateboard.

  • Vereinfachtes Schnittbild des Menschen[2].
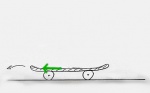
    Er wird nach vorne gedrückt.

  • Vereinfachtes Schnittbild des Skateboards mit der Erde[3].
    Das Skateboard wird nach hinten gedrückt.


Ein Wagen fährt auf zwei stehende Wagen und kuppelt ein.


Dies kann man mit drei zeitlichen Phasen beschreiben:

vorher
Beide Gegenstände haben zusammen den Impuls [math]\vec p + \vec P[/math]
Änderung
Eine Zeit [math]t[/math] lang wirkt auf den Gegenstand eine mittlere Kraft [math]\vec F[/math] und auf den Partner die gleichgroße, aber entgegengesetzt wirkende Gegenkraft [math]-\vec F[/math].
Der Gegenstand erhält also den Impuls [math]\triangle \vec p = \vec F \cdot t[/math] und der Partner verliert ihn, bzw. bekommt den Impuls [math]-\triangle \vec p[/math][4].
nachher
Beide Gegenstände haben ihren Impuls verändert, aber zusammen haben sie immer noch den gleichen Impuls: [math]\vec {p'} + \vec {P'}[/math]


Rechnung

Als Rechenansatz gibt es zwei Möglichkeiten:

Impulsbilanz
Man setzt den Impuls vor und nach dem Impulsaustausch gleich:
[math]p+P = p'+P'[/math]
Falls die Masse der Gegenstände sich nicht verändert, gilt:
[math]m \, v + M \, V = m \, v' + M \, V' [/math]
Nun überlegt man sich, welche Größen gegeben sind und welche Größe nicht. Nach der unbekannten Größe löst man auf.
Impulsänderung
Der Impuls ändert sich bei einer zeitlich konstanten Kraft um [math]\Delta \vec p = \vec F \cdot \Delta t[/math].
Für die Impulse nach dem Kontakt gilt also:
[math]\vec {p'} = \vec p + \Delta \vec p \quad \text{und} \quad \vec {P'} = \vec P - \Delta \vec p [/math]
Bei unveränderten Massen folgt daraus:
[math]m \, \vec {v'} = m \, \vec v + \Delta \vec p \quad \text{und} \quad M \, \vec {V'} = M \, \vec V - \Delta \vec p [/math]
Teilt man die Gleichungen noch durch die jeweilige Masse, so kann man die Geschwindigkeiten nach dem Impulsaustausch berechnen:
[math]\vec {v'} = \vec v + \frac{1}{m}\,\Delta \vec p \quad \text{und} \quad \vec {V'} = \vec V - \frac{1}{M}\, \Delta \vec p [/math]

Fußnoten

  1. ↑ Das gilt eigentlich nur für Achsen, bezüglich der Körper keine Unwucht hat, der sogenannten "Hauptträgheitsachsen". Für Drehachsen, die auch eine Symmetrieachse des Körpers sind, hat der Körper keine Unwucht. Ist im Abstand r von der Achse die Masse m verteilt, so beträgt das Trägheitsmoment [math]\Theta = m\, r^2[/math].
  2. ↑ Es fehlt die Gewichtskraft sowie die Kraft mit der das Skateboard nach oben gegen die Füße des Menschen drückt.
  3. ↑ Es fehlt die Kraft mit der die Erde zum Menschen gezogen wird, sowie die Kraft mit der die Füße des Menschen nach unten gegen das Skateboard drücken.
  4. ↑ Die Menge des übertragenen Impulses wird auch "Kraftstoß" genannt.

Links

  • Wikipedia:Tischtennisball Geschwindigkeit, Masse und Länge des Aufpralls
veraltet
Einfache Methoden zur Messung von Roll- und Luftwiderstandsbeiwert am Fahrrad (von Alfons Kolling)
Von „http://schulphysikwiki.de/index.php?title=Kraft_und_Impuls&oldid=14980“